Ступенчатый регрессионный метод

Метод включений

  Уравнение регрессии характеризует взаимосвязь между переменными x и y в том смысле, что показывает, как изменяется величина y в зависимости от изменения величины x. Однако в самом уравнении регрессии с оцененными параметрами нет указания на то, как близко находятся фактические наблюдения от расчетных (полученных по регрессии), иначе говоря, нет указания на степень тесноты связи между переменными. Поэтому оценка параметров регрессии обычно сопровождается расчетом такой дополнительной характеристики, как коэффициент корреляции, который представляет собой эмпирическую меру линейной зависимости между x и y.

Коэффициент корреляции для некоторой выборки значений x и y определяется по формуле использованием уже рассчитанных формул (1.7 и 1.8)

 

                            (1.36)

 

где

                                                          (1.37)

                                                          (1.38)

                                           (1.39)

                                           (1.40)

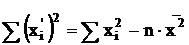                                          (1.41)

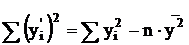                                          (1.42)

 

Величина r_{x , y} лежит между -1 и 1. Чем выше значение r_{x , y}, тем теснее связь между переменными и тем с большим основанием найденная взаимосвязь может быть использована для прогнозирования.

Метод включения состоит в том, что в уравнение включаются переменные по степени их важности до тех пор, пока уравнение не станет достаточно «хорошим». Степень важности определяется линейным коэффициентом корреляции, показывающим тесноту связи между анализируемой независимой переменной и результативным признаком: чем теснее связь, тем больше информации о результирующем признаке содержит данный факторный признак и тем важнее, следовательно, введение этого признака в уравнение.

Процедура начинается с отбора факторного признака, наиболее тесно связанного с результативным признаком, т. е. такого факторного признака, которому соответствует максимальный по величине парный линейный коэффициент корреляции. Далее строится линейное уравнение регрессии, содержащее отобранную независимую переменную. Выбор следующих переменных осуществляется с помощью частных коэффициентов корреляции, в которых исключается влияние вошедших в модель факторов. Для каждой введенной переменной рассчитывается частный F -критерий, по величине которого судят о том, значим ли вклад этой переменной. Как только величина частного F -критерия, относящаяся к очередной переменной, оказывается незначимой, т. е. эффект от введения этой переменной становится малозаметным, процесс включения переменных заканчивается. Метод включения связан с меньшим объемом вычислений, чем предыдущие методы. Но при введении новой переменной нередко значимость включенных ранее переменных изменяется. Метод включения этого не учитывает, что является его недостатком.

Основные шаги этого метода сводятся к следующему.

1. Вычисляется линейный коэффициент корреляции (1.36)

2. Находятся

3. Строится уравнение регрессии  (наиболее сильно коррелированной переменной)

4. Находится наблюдаемый F – критерий и сравнивается с критическим F – критерием.

5. Вычисляется частный коэффициент корреляции

6. Находятся

7. Строится уравнение регрессии

8. Находится наблюдаемый F – критерий и сравнивается с критическим F – критерием. Если F_набл<F_кр расчет прекращается. Если нет, то расчет продолжается, и повторяются предыдущие пункты.

Контрольный пример

    Данные для расчета по методу исключений возьмем из предыдущего раздела (раздел 1.2.1.1 из  табл. 1.1).

Сделаем пример для r_x1y, расчеты выполняются по формулам (1.7, 1.8, 1.34, 1.35, 1.36)

 

 

 

 

 

       

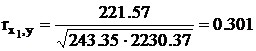
   Остальные расчеты ведутся аналогично и имеем

 

                  

 

                  

 

                  

       

   Выбираем х₂, и составляем уравнение регрессии

 

                       

                  

 

   Проверяем по F – критерию и имеем F_набл=33,3>F_кр=4,45

   Выполняем расчет частный коэффициент корреляции  и имеем:

 

              

 

                  

 

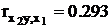
   Выбираем х₃, и составляем уравнение регрессии

 

                       

                  

 

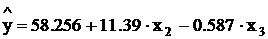
   Проверяем по F – критерию и имеем F_набл=8,8>F_кр=3,63

   Выполняем расчет частный коэффициент корреляции  и имеем:

 

              

 

Так как связь между показателями мала, то переменную х₁, отвергаем и имеем окончательное уравнение регрессии

 

            

 

 

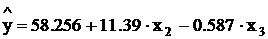
Ступенчатый регрессионный метод

 

Ступенчатый регрессионный метод включает в себя такую последовательность действий. Сначала выбирается наиболее тесно связанная с результативным признаком переменная и составляется уравнение регрессии. Затем находят разности фактических и выровненных значений и эти разности (остатки) рассматриваются как значения результативной переменной. Для остатков подбирается одна из оставшихся независимых переменных и т. д. На каждой стадии проверяется значимость регрессии. Как только обнаружится незначимость, процесс прекращается и окончательное уравнение получается суммированием уравнений, полученных на каждой стадии за исключением последней.

Основные шаги этого метода сводятся к следующему.

1. Вычисляется линейный коэффициент корреляции (1.36)

2. Находятся

3. Строится уравнение регрессии 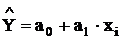 (наиболее сильно коррелированной переменной)

4. Вычисляем остатки для каждого значения Xi

5. Остатки V_i рассматриваем, как новые отклики и выбираем из оставшихся переменных ту, которая сильно коррелированна с этими остатками

6. Строится уравнение регрессии, связывающее V_i с выбранной новой переменной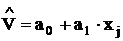

7. Записываем полное уравнение регрессии на втором этапе, как  

8. Проверяется значимость новой переменной в полученном уравнении по F - критерию. Если переменная незначима, то расчет прекращается, в противном же случае, снова вычисляются остатки и повторяются пункты 4-8

Контрольный пример

    Данные для расчета по методу исключений возьмем из предыдущего раздела (раздел 1.2.1.1 из  табл. 1.1).

Расчет линейных коэффициентов корреляции выполняется так же как в предыдущем пункте (1.2.1.4).

 

       

 

          

 

          

 

   Наиболее сильно коррелированна переменная х2, строим уравнение регрессии относительно нее

 

          

 

   Проверяем по F – критерию и имеем F_набл=33,3>F_кр=4,45

Вычисляем остатки и ищем переменную наиболее сильно коррелированную с ними

               

          

 

          

 

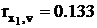
   Наиболее сильно коррелированна переменная х₃, поэтому строим уравнение регрессии, связывающее остатки с этой переменной

               

          

 

  Записываем полное уравнение регрессии на этом этапе

 

    

Проверяем по F – критерию и имеем F_набл=32,0>F_кр=3,63

Вычисляем остатки и ищем переменную наиболее сильно коррелированную с ними

 

    

 

Так как х₁ слабо коррелирован то расчет прекращаем и имеем окончательное уравнение регрессии