3.3.1. Законы теплового излучения
Длина волны инфракрасного излучения (ИКИ) лежит в границах от 0,76 мкм до 1 мм. Самый мощный источник ИКИ — Солнце, около 50% его излучения лежит в ИК области спектра. Все нагретые жидкие и твёрдые тела испускают ИКИ со сплошным спектром.
При взаимодействии с веществом ИКИ вызывает колебания ионов. С другой стороны существует ИК тепловое излучение, испускаемое веществом и возникающее за счёт его внутренней энергии. Оно находится в термоди-намическом равновесии с веществом. Равновесное излучение изотропно, т.е. оно не поляризовано и все направления его распространения равновероятны.
Благодаря требованию термодинамического равновесия тепловое излучение противопоставляется всем прочим видам электромагнитного излучения. Оно присуще всем нагретым телам, имеющим отличную от абсолютного нуля температуру. Излучаемая при этом энергия характеризуется распределением по частотам или длинам волн. Человеческий организм представляет собой пример тела, излучающего, с одной стороны, в полном соответствии с классическими законами теплового излучения, с другой — не требующего специальных источников тепла для осуществления теплового равновесия. В этом плане (чисто тепловом) организм человека и млекопитающих является уникальным объектом, температура которого практически не меняется при изменении окружающих условий.
Энергетической светимостью (интегральной испускательной способностью) тела называется физическая величина R э, численно равная энергии электромагнитных волн 
всевозможных частот (или длин волн) от 0 до ∞, излучаемых за единицу времени с единицы площади поверхности тела
, (3.13)
где 
— испускательная способность.
Испускательная способность r l — это спектральная плотность потока лучистой энергии, излучаемого с единицы площади поверхности тела. Но поток энергии с единицы площади — это энергетическая светимость тела. Следовательно, испускательная способность — это спектральная плотность энергетической светимости тела. Введенная таким образом r l не зависит от того, находится ли данное тело в равновесии с излучением или нет. В ряде случаев требуется исследовать зависимость испускательной способности не от длины волны, а от частоты n. В этом случае r n — это величина, приходящаяся не на единицу длины волны, а на единицу частоты. Имея в виду, что 
(дифференциальный поток), а также выражая
,
запишем соотношение
, (3.14)
которое полезно для перехода от частоты к длине волны при записи формул, описывающих законы теплового излучения.
Поглощательной способностью (монохроматическим коэффициентом поглощения) тела называется безразмерная величина а n, показывающая, какая доля энергии электромагнитных волн с частотами от n до n + d n, падающих на поверхность тела, поглощается им:
. (3.15)
Поглощательная способность а n зависит от частоты, температуры, химического состава тела и состояния его поверхности.
Абсолютно чёрным телом (АЧТ) называют тело, которое полностью поглощает всё падающее на него излучение независимо от направления падающего излучения, его спектрального состава и поляризации, ничего не отражая и не пропуская: а n = 1. Примером абсолютно чёрного тела может служить ротовая полость, ушное отверстие, глаз и др. Серым телом называется тело, поглощающая способность которого меньше 1 и не зависит от частоты (длины волны) света, направления его распространения и поляризации. Для реальных тел испускательная способность r l всегда меньше, чем r l* для АЧТ при той же температуре. Спектральным коэффициентом излучения для данного тела (коэффициентом серости) называется отношение
,
которое можно также рассчитать по формуле
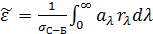, (3.16)
|
где s С-Б» 5.67·10-8 Вт/(м2·К4) — постоянная Стефана-Больцмана.
Большинство тел при Т = 290…330 К можно считать серыми. Для ИК области спектра тело человека является серым с коэффициентом 
» 0,9, поэтому его можно с достаточной степенью точности считать черным независимо от цвета кожи.
Вопросу о связи между излучательной и поглощательной способностями давно уделялось пристальное внимание со стороны исследователей. Длительные экспериментальные и теоретические изыскания привели к термодинамическому толкованию этой связи в форме закона Кирхгофа — отношение испускательной способности тела к его поглощательной способности не зависит от природы тела и равно испускательной способности АЧТ r *n, при тех же значениях температуры и частоты
; 
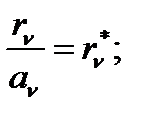
(3.17)
Чёрное тело при прочих равных условиях является наиболее интенсивным источником теплового излучения.
| Йозеф Стефан (1835-1893) Австрийский физик, член Австрийской АН (1865). Профессор (с 1863), ректор (1876...1877) Венского университета. Основатель австрийской школы физиков. Труды в области оптики, акустики, электромагнетизма, кинетической теории газов. Экспериментально установил зависимость энергии, излучаемой нагретым телом, от четвертой степени температуры (1879), позднее (1884) теоретически объясненную Больцманом. |
Кирхгоф сформулировал этот закон в форме теоремы, доказанной им на основе термодинамических соображений. Теорема Кирхгофа, отражающая фундаментальное свойство теплового излучения, не позволяет установить точный вид функции
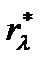( l ,T), а для практических целей это совершенно необходимо.
Дальнейшие исследования позволили установить (В.Вин, 1893 г.), что функция 
( l ,T) может быть представлена в виде
(3.18)
| Вильгельм Вин (1864-1928) Немецкий физик, член-корр. Берлинской АН. Профессор Вюрцбургского (1900-20), Мюнхенского (1920-28) университетов. Работы в области теплового излучения, оптики, термо- и гидродинамики, физики газового разряда. Предложил совместно с О. Люммером модель черного тела в виде полости с малым отверстием. За работы по теории теплового излучения удостоен Нобелевской премии (1911). |
Сообразно своему определению, величина r l имеет следующую размерность: Вт×м–2×мкм–1, т.е. размерность спектральной плотности потока излучения, испускаемого с единичной площадки. Установим связь между r l и спектральной плотностью энергии равновесного излучения. Пусть имеется некоторая замкнутая полость, заполненная электромагнитным излучением со средней спектральной плотностью U l (с размерностью Дж×м-3×мкм-1). Выделим на внутренней поверхности, окружающей данную полость, площадку d S = 1 (рис. 3.19). В направлении q и j в пределах телесного угла d W = sinq d q d j распространяется доля d W / 4p от всей энергии, заполняющей полость. Поток энергии, проходящей через единичную площадку в единицу времени
(3.19)
Интегрируя (3.19) в пределах от 0 до 2p по j и от 0 до p/2 по q, получим полный поток энергии, проходящей через единичную площадку d S:
Полагая, что тело, окружающее полость, является абсолютно черным (а l º 1), можно приравнять эту величину к дифференциальному потоку, испускаемому этой площадкой:
(3.20)
Соотношение (3.20) позволяет вычислить r l или r n, опираясь на модель взаимодействия с внешним полем осциллятора, моделирующего среду. В дальнейшем удобно перейти к записи спектральной плотности излучения не через λ, а через ν, используя формулу:
аналогично соотношению между r l и r n в (3.14).
Осциллятор среды, находясь во внешнем поле со спектральной плотностью U n, поглощает от него мощность, определяемую выражением
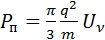. (3.21)
Здесь q – заряд, m – масса колеблющейся заряженной частицы (осциллятор, напомним, рассматривается как электрический диполь с моментом 
, 
– размер диполя).
В то же время, как всякий ускоренно движущийся заряд, осциллятор излучает по всем направлениям мощность
(3.22)
где á ε ñ – средняя энергия, приходящаяся на одну колебательную степень свободы осциллятора. Приравнивая (3.21) и (3.22), получим выражение для U n:
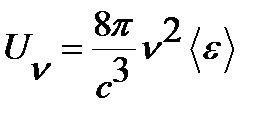
Используя (3.20), запишем:
(3.23)
Формула (3.23), опирающаяся на закон Кирхгофа и классические соотношения для осциллятора, взаимодействующего с внешним полем, не подлежит сомнению с точки зрения самых общих принципов термодинамики и электродинамики. Не менее общий характер носит формула
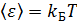(3.24)
являющаяся следствием принципа равнораспределения энергии по степеням свободы в состоянии термодинамического равновесия. Объединяя (3.23) и (3.24), получаем классическую формулу Рэлея–Джинса:
(3.25)
Очевидно, (3.25) удовлетворяет форме (3.18), в чем нетрудно убедиться, положив
В такую запись F( n /T) входят, как видно, универсальные константы — постоянная Больцмана и скорость света. Используя соотношение (3.17), получим выражение формулы Рэлея–Джинса через r l:
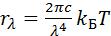(3.26)
Формула Рэлея–Джинса согласуется с экспериментом только при достаточно больших значениях произведения l Т: если l Т > 7,8×105 мкм×К, то (3.26) дает расхождение с экспериментом не более 1 %. В частности, если принять Т» 306 К (средняя температура поверхности тела человека), то (3.26) дает ошибку не более 1% только при l > 2500 мкм. При l ® 0 r l ® ¥ при любой температуре, а интеграл (3.16) расходится, хотя бесконечная светимость при конечных размерах тела не имеет физического смысла. Это расхождение между экспериментом и классически безупречной теорией, приводящей к формуле Рэлея–Джинса, получило название ультрафиолетовой катастрофы. Все попытки объяснить его не имели успеха, пока не появилась гипотеза Планка о том, что энергия осциллятора не может принимать произвольные значения, а всегда кратна некоторой определенной минимальной величине (кванту). Наиболее изящно применил эту гипотезу Эйнштейн, идее которого при выводе формулы для r l(r n) мы и последуем (рис. 3.20).
| Рис. 3.20. К выводу формулы Планка по Эйнштейну. |
1. 
— спонтанное излучение с вероятностью перехода Аmn с уровня с номером m на уровень с номером n (m ® n)в единицу времени с появлением кванта h n, дающего вклад в спектральную плотность энергии U n поля.
2. 
— вынужденное поглощение n ® m с вероятностью перехода Вnm в единицу времени с исчезновением кванта h n. Поглощение n ® m называется вынужденным, поскольку оно происходит под действием поля: если U n = 0, то и поглощения нет. В равновесии населенности уровней определяются по Больцману:
; 
.
Поскольку ε m > ε n, Nm < Nn. Поэтому при наличии только процессов 1 и 2 термодинамическое равновесие в системе вещество–излучение невозможно. Эйнштейн предположил наличие третьего процесса — вынужденного излучения:
3. 
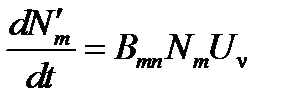, с соответствующей вероятностью перехода Bmn.
| Альберт Эйнштейн (1879-1955) Физик-теоретик, один из величайших физиков всех времен. Является одним из основоположников современной физики. Известен прежде всего как автор специальной и общей теории относительности. Эйнштейн внес также значительный вклад в создание квантовой механики и квантовой теории излучения, развитие статистической физики и космологии. Лауреат Нобелевской премии по физике (1921) за работы по объяснению фотоэлектрического эффекта. |
В термодинамическом равновесии должно выполняться соотношение dNm + dN'm = dNn. Тогда из уравнения баланса
получим
.
Подставляя в это выражение Nm и Nn с учётом закона Больцмана, запишем
.
Требуя, чтобы U n ® 0при Т ® ¥, получим Bnm = Bmn, поскольку в противном случае выполнить это требование невозможно. Тогда выражение для U n принимает вид
(3.27)
Применим принцип соответствия: при h n << k Б T формула (3.27) должна превращаться в формулу Рэлея–Джинса, а также удовлетворять формуле Вина. Последнее возможно только в случае: Amn/Bmn = an 3 ( a = const).
Константа a находится из условия соответствия формуле Рэлея–Джинса при h n/ k Б T << 1:
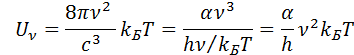
Отсюда a = 8p h / c3 и, окончательно,
(3.28)
(3.29)
| Рис. 3.21. Положение максимума испускательной способности абсолютно чёрного тела при различных температурах. |
(3.30)
Теоретическая кривая r l(l), построенная по формуле Планка обнаруживает полное соответствие с экспериментальной кривой, нарушающееся только при отличии реального тела от абсолютно черного. Вид зависимости r l(l) при различных Т показан на рис. 3.21.
Формула Планка превращается, как и положено, в формулу Рэлея–Джинса при hc/ l k Б T <<1, если разложить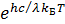 
в ряд. Если же выполнено обратное соотношение hc/ l k Б T >> 1, то единицей в знаменателе (3.30) можно пренебречь, в итоге чего получаем формулу Вина, также полученную до Планка как полуэмпирическую:
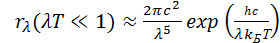(3.31)
Формула Вина дает точность не хуже 1 % при значениях произведения l Т < 3×103 мкм×К. При Т = 306 К она справедлива, если l < 10 мкм.
Дифференцируя формулу Планка и приравнивая производную нулю, получим условие для нахождения положения максимума кривой:
Обозначая 
, получим трансцендентное уравнение относительно х max:
.
Правая часть имеет вертикальную асимптоту при x max = 5. Левая часть быстро возрастает, при x max = 5 имеем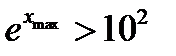 
. Поэтому с точностью не хуже 1% можно принять x max» 5, т.е. для l max получаем:
или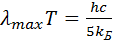 
(3.32)
Выражение (3.32) обычно записывается в виде
(3.33)
где b = 2,9·10-3 м·К, и называется законом смещения Вина, подчеркивая тот факт, что при росте температуры Т максимум кривой Планка смещается в сторону коротких волн. На рис. 3.21 это смещение показано пунктиром. Для уже упоминавшейся температуры Т = 306 К максимум r l приходится на длину волны lmax» 9,47 мкм. Из рисунка видно, что АЧТ почти не излучает в области очень малых и очень больших частот.
Интегрирование распределения Планка дает интегральную испуска-тельную способность, при вычислении которой удобнее работать с r n, а не r l:
Выделяя Т 4, придем к закону Стефана–Больцмана:
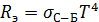(3.34)
где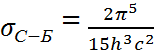 
= 5,67·10-8 Вт/(м2·К4) — постоянная Стефана-Больцмана.
Приведём некоторые значения максимальных длин волн ИК излучения различных объектов:
lmax» 8...14 мкм (для атмосферы вблизи поверхности Земли);
lmax » 9,5 мкм (для поверхности кожи человека);
lmax = 470 нм (для Солнца на границе земной атмосферы). Такая длина волны соответствует температуре поверхности Солнца 6100° С.
lmax = 555 нм (на поверхности Земли при наивысшем стоянии Солнца).
3.3.2. Тепловая рецепция и терморегуляция
Если какой-то сигнал вызывает изменение в активности или поведении животных, он называется стимулом (раздражителем). Специальные органы или клетки, воспринимающие стимулы, называются рецепторами. Животные воспринимают стимулы в виде одного из видов энергии: электромагнитной, механической, тепловой, химической. Структуры, преобразующие энергию раздражителя в электрические сигналы, возникающие в аксоне, называются преобразователями, и в этом смысле рецепторы действуют как биологические преобразователи.
В дерме имеются два типа рецепторов, которые обычно считают ответственными за температурную чувствительность. Полагают, что на тепло реагируют тельца Руффини, а на холод — колбочки Краузе. Однако главными температурными рецепторами кожи скорее всего являются многочисленные свободные нервные окончания в эпидермисе и дерме.
Главным источником тепла для всех живых существ служит солнечная энергия. Температура является показателем количества тепловой энергии в сис-теме и основным фактором, определяющим скорость химических реакций как в живых, так и в неживых системах. В живых системах температура влияет на структуру ферментов, которая в свою очередь влияет на интенсивность обмена.
Кроме непосредственного получения тепла из внешней среды, животные получают тепло из химических субстратов, подвергшихся расщеплению в клетках. Птицы и млекопитающие способны поддерживать достаточно постоянную температуру тела, независимо от окружающей температуры. Они относительно мало зависят от внешних источников тепла, т.к. благодаря высокой интенсивности обмена, у них вырабатывается достаточное количество тепла, которое может сохраняться.
Когда говорят о температуре биообъекта, обычно имеют в виду темпера-туру внутренних областей тела, т.е. тканей лежащих глубже 2,5 см под поверх-ностью кожи. Температура различных участков тела может сильно изменяться в зависимости от их локализации и от наружной температуры. В основном, чем дальше от верхнего края таза, тем меньше температура участка тела.
Способы теплообмена между организмом и окружающей средой включают излучение, конвекцию, теплопроводность и испарение. С помощью первых трёх способов тепло может передаваться в любом направлении в зависимости от температурного градиента, при четвёртом способе организм может только терять тепло. Кратко охарактеризуем эти способы теплообмена.
Излучение – перенос теплоты в виде электромагнитных волн ИК-части спектра. У человека на излучение приходится около 50% общей теплоотдачи.
Конвекция – передача теплоты от организма окружающей среде через воздух. Скорость передачи теплоты этим способом зависит от скорости движения воздуха около поверхности тела. Она может быть снижена за счёт материалов, покрывающих кожу (перья у птиц, мех у животных, волосы, одежда у человека). В условиях умеренного климата конвекция составляет 15...20% теплоотдачи.
Теплопроводность – передача теплоты при физическом контакте между телами (организм-земля и др.).
Испарение – потеря теплоты с поверхности тела в процессе превращения воды в водяной пар. Испарение идёт через кожу и в лёгких с выдыхаемым воздухом. Эффективность теплоотдачи через испарение существенно превосходит перечисленные выше прочие способы, поскольку здесь имеет место фазовый переход.
Скорость теплоотдачи зависит от разности температур между внутренними областями тела и его поверхностью и между кожей и окружающей средой; от скорости образования тепла и от внешней температуры. Факторами, ограничивающими теплоотдачу, являются: скорость кровотока в коже, потоотделение и испарение через кожу.
Тепловой баланс любого тела определяется соотношением между теплом, которое оно получает, и теплом, которое оно отдаёт. У теплокровных животных равенство прихода и расхода тепла всегда сохраняется. Система терморегуляции включает рецепторы, эффекторы и регуляторный центр в гипоталамусе. Эффектор — это дифференцированная структура (клетка, ткань, орган или система органов), осуществляющая специфическую реакцию в ответ на стимулы, поступающие из нервной системы. Центр в гипоталамусе следит за температурой крови, отражающей температуру тех органов, через которые она протекает. Он также получает через терморецепторы информацию о температуре окружающей среды.
Тепловой баланс каждого участка тела поддерживается путём теплоре-гуляции за счёт генерации тепла вследствие метаболизма; обмена теплом с соседними участками тела из-за термодиффузии; конвективного теплообмена посредством кровотока, т.е. за счёт притока и оттока тепла с кровью.
Вычислим теплопотери человека в результате ИКИ. Для этого сделаем два допущения: излучающие тела (кожа человека, ткань одежды) примем за серые; применим закон Стефана-Больцмана к неравновесному излучению, каковым является излучение тела человека.
Пусть раздетый человек, поверхность тела которого имеет температуру Т 1, находится в комнате с температурой Т 0. Тогда согласно закону Стефана-Больцмана человек излучает со всей открытой поверхности тела площади S мощность Р 1 = S 
sС-Б T 14, где 
— коэффициент серости тела. Одновременно человек поглощает часть излучения, падающего от предметов комнаты, стен, потолка и т.д. Если бы поверхность тела человека имела температуру, равную температуре воздуха в комнате, то излучаемая и поглощаемая мощности были бы одинаковы и равны Р 0 = S 
sС-Б T 04. Такая же мощность будет поглощаться телом человека и при других температурах поверхности тела, следовательно, мощность, теряемая человеком при взаимодействии с окружающей средой посредством излучения
Р Σ = Р 1 – Р 0 = S 
sС-Б (T 14 – T 04 ) (3.35)
Если необходимо посчитать мощность в некоторый телесный угол W, то формула (3.35) переходит в
Р Σ(W) = S 
sС-Б (T 14 – T 04 ) ·(W/2p).
При Т 0 = 18°С (Т 0=291 К) раздетый человек, температура кожи которого 33°С (T 1=306 К), теряет в 1 с посредством излучения с площади 1,5 м2 энергию Р Σ= 122 Дж, а в хлопчатобумажной одежде, температура поверхности которой 24°С (T 1=297 К), — Р Σод=37 Дж.
3.3.3. Воздействие высоких температур на биоткани.
При излишнем нагревании биоткани могут происходить денатурация, коагуляция белка, деструкция биоткани (табл. 3.1).
Денатурация белка заключается в утрате трёхмерной конформации данной молекулы, однако аминокислотная последовательность при этом сохраняется. При денатурации молекула белка теряет способность выполнять свою обычную биофункцию. Вызвать денатурацию могут также ИИ, однако характер денату-рации в тепловом и ионизирущем случаях различен: денатурация при воздейст-вии ИИ носит локальный характер (разрушение связей в биомолекулах высоко-энергичными фотонами), а при тепловом воздействии имеет место существенно коллективный эффект: средняя кинетическая энергия биомолекул становится настолько большой, что трехмерная конформация оказывается невозможной.
При дальнейшем повышении температуры кинетическая энергия, сообщаемая белку, вызывает сильную вибрацию его атомов, вследствие чего слабые водородные и ионные связи разрываются. Белок свёртывается (коагулирует), испытывая фазовое превращение второго рода: основная структура живого (и даже денатурированного) белка представляет собой жидкий кристалл, а скоагулированного — гель.
Воздействие высоких температур может привести к деструкции (полному разрушению) биоткани.
Такие тепловые биологические эффекты при нагревании биоткани применяются в медицине (в основном испарение (резание) и коагуляция биоткани) при гипертермии и в лазерной хирургии. Для этого используются различные лазеры с плотностью мощности от 1 до 107 Вт/см2 и с продолжительностью облучения от 10-3 с до нескольких секунд. В зависимости от оптических свойств биоткани при применяемой длине волны необходимые температуры в ткани могут быть достигнуты с различными уровнями мощности и длительности облучения. Так, например, при кратковременном нагревании в течении 1 с до 70° С биоткань разрушается точно так же, как при нагревании в течение 10 секунд до 58°С.
Таблица 3.1. Изменения в мягких биотканях при повышении температуры
| Температура, °С | Эффект на биотканях |
| 37 | Нет необратимых повреждений |
| 40-45 | Активация ферментов, образование отёков, изменение мембран и, в зависимости от времени, денатурация белков |
| 60 | Денатурация протеина, начало коагуляции и некрозы |
| 80 | Денатурация коллагена, разрушение мембран |
| 100 | Обезвоживание (выпаривание выделившихся в результате разрушения мембран биожидкостей) |
| >150 | Обугливание (химическое разложение биотканей с выделением свободного углерода) |
| >300 | Выпаривание, сублимация — переход из твердой фазы в газообразную с образованием кратеров и разрезов в тканях |
Преобразование энергии оптического излучения, в том числе и лазерного, в теплоту может произойти, если оно поглощается специфическими хромофорами ткани, причём не обязательно хромофорами пигментов, например, для СО2-лазера с l=10,6 мкм таким хромофором является вода. Плотность энергии источника теплоты q (Вт/м3) в облучаемом объёме ткани является функцией коэффициента поглощения и общей плотности потока энергии облучения Ľ (
, которая состоит из непосредственно падающей части коллимированного лазерного пучка Ľ c( и из доли Ľ s(, привходящей при рассеянии из окружающих тканей:
[ Ľ c ( + Ľ s 
],
где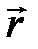 
— радиус-вектор точки наблюдения, t — время. Превращённая в теплоту энергия приводит к локальному повышению температуры; если при этом нет фазовых переходов, то температура растёт в первом приближении пропор-ционально q (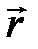, t). Часть тепла отводится путём теплопроводности и локальным кровотоком в более холодные участки. Из-за этого ограничивается максималь-но достижимая температура при данной интенсивности излучения. Для каждой ткани, кроме того, существует специфический порог интенсивности, который необходим для достижения необходимой температуры.
Тепловой поток в тканях
, (3.35)
где g — коэффициент пропорциональности; в зависимости от содержания воды g» 0,3…0,5: 
, w — содержание воды в ткани, кг/м3, r — плотность ткани, кг/м3, l — длина образца c поперечным сечением S, Т 1 > T 2. Способность ткани накапливать теплоту описывается через удельную теплоёмкость 
. В табл. 3.2 даны значения коэффициента пропорциональности g при нормальных условиях (н.у.) и теплоёмкости С для различных тканей.
Общая пространственная и временная характеристика температурного распределения в облучённом объёме ткани даётся классическим уравнением теплопроводности: 
, где Ñ2 — оператор Лапласа.
Таблица 3.2
| Вид биоткани | Коэффициент пропорциональности g
при н.у.,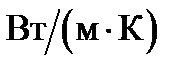 
| Теплоёмкость С,
|
| Жировая ткань | 0,3 | 1,93 |
| Водосодержащая ткань (эпителий) | 0,5 | - |
| Вода | 0,58 | - |
| Кровь | 0,62 | 3,22 |
Для практического расчёта временной характеристики распространения локального нагревания параметром является время термической релаксации 
. Физический смысл этой величины таков: если на поверхность ткани подаётся короткий импульс тепла, то должно пройти время порядка t, чтобы на глубине 
произошло повышение температуры на величину, заведомо превосходящую температурные флуктуации при исходном гомеостазе организма.
Влиянием кровотока по сосудам в облучаемом объёме на температурное распределение нельзя пренебрегать, если время облучения порядка или больше времени перфузии (время, за которое заменяется вся кровь в единице объёма). Это особенно важно при непрерывном облучении, когда время внешнего воздействия может оказаться большим.
[1] См. определение понятия спектр биологического действия в 3.1.
[2] АТФ – аденозинтрифосфат, АДФ – аденозиндифосфат, Ф- фосфат.
