При изучении различных физических явлений применяют два метода исследований, которые позволяют получить количественные закономерности для рассматриваемых явлений. В первом методе используют экспериментальное изучение конкретных свойств, единичного, явления, во втором исходят из теоретического исследования рассматриваемой проблемы.
Достоинством экспериментального метода исследования является достоверность получаемых результатов. Кроме того, при выполнении эксперимента основное внимание можно сосредоточить на изучении величин, представляющих наибольший практический интерес.
Основной недостаток экспериментального метода заключается в том, что результаты данного эксперимента не могут быть использованы применительно к другому явлению, которое в деталях отличается от изученного. Поэтому выводы, сделанные на основании анализа результатов данного экспериментального исследования, не допускают распространения их на другие явления.
Второй метод исследования для нахождения количественных зависимостей, который широко применяется современной наукой, рассматривается в математической или теоретической физике.
При выводе дифференциальных уравнений теоретической физики используются самые общие законы природы. Приложение этих законов к изучаемым явлениям позволяет получить наиболее общие связи между физическими параметрами, характеризующими явления.
Любое дифференциальное уравнение (или система уравнений) является математической моделью целого класса явлений. Под классом понимается такая совокупность явлений, которая характеризуется одинаковым механизмом процессов и одинаковой физической природой.
Явления, которые входят в класс, подчиняются одинаковым уравнениям, как по форме записи, так и по физическому содержанию входящих в него величин.
При интегрировании любого дифференциального уравнения можно получить бесчисленное множество различных решений, удовлетворяющих этому уравнению.
Чтобы из множества решений получить одно частное, надо знать все характерные особенности данного явления, выделяющие его из всего класса однородных явлений. Эти дополнительные условия, которые вместе с дифференциальным уравнением однозначно определяют единичное явление, называют условиями однозначности.
Условия однозначности состоят из: 1) геометрических условий, характеризующих форму и размеры тела или системы; 2) физических условий, которыми обладают тела, составляющие данную систему; 3) граничных условий, которые характеризуют взаимодействие системы с окружающей средой; 4) временных условий, характеризующих протекание процесса в начальный момент времени (для стационарных процессов временные условия отпадают).
В большинстве случаев и, в частности, в случае конвективного теплообмена из-за сложности изучаемых явлений найти решение, удовлетворяющее дифференциальным уравнениям и условиям однозначности, невозможно.
Следовательно, если недостатком экспериментального метода исследования является невозможность распространения результатов, полученных в данном опыте, на другие явления, отличающиеся от изученного, то недостатком математической физики является невозможность перейти от класса явлений, характеризуемых дифференциальными уравнениями и условиями однозначности, к единичному конкретному явлению. Каждый из этих методов в отдельности не может быть эффективно использован для решения практических задач.
Если положительные стороны математического и экспериментального методов исследования объединить в одно целое, то можно получить универсальный аппарат для изучения различных явлений природы. Такое объединение обоих методов осуществляется теорией подобия.
Подобными явлениями называются такие физические явления, которые одинаковы качественно по форме и по содержанию, т.е. имеют одну физическую природу, развиваются под действием одинаковых сил и описываются одинаковыми по форме дифференциальными уравнениями и краевыми условиями.
Обязательным условием подобия физических явлений должно быть геометрическое подобие систем, где эти явления протекают. Два физических явления будут подобны лишь в том случае, если будут подобны все величины, которые характеризуют их.
Для всех подобных систем существуют безразмерные комплексы величин, которые называются критериями или числами подобия.
Основные положения теории подобия формулируют в виде 3-х теорем подобия.
1 теорема: Подобные явления имеют одинаковые числа подобия.
2 теорема: Любая зависимость между переменными, характеризующая какие-либо явления, может быть представлена, в виде зависимости между числами подобия, составленными из этих переменных. Эта зависимость называется критериальным уравнением.
3 теорема: Подобны те явления, условия однозначности которых подобны, и числа подобия, составленные из условий однозначности, численно равны.
Числа подобия, составленные из величин, входящих в условия однозначности называются определяющими. Числа подобия, в которые входят искомые величины, называются определяемыми.
Конкретные числа подобия получают в результате анализа дифференциальных уравнений описывающих изучаемое явление. Применительно к конвективному теплообмену наиболее распространены числа подобия представленные в таблице:
| Название | Символ | Определение числа | Физическое содержание |
| Число Нуссельта | Nu | 
| Безразмерный коэффициент теплоотдачи. Характеризует связь между интенсивностью теплоотдачи и температурным полем в пограничном слое потока. |
| Число Рейнольдса | Re | 
| Мера отношения сил инерции и вязкости в потоке жидкости. Определяет режим течения жидкости. |
| Число Грасгофа | Gr | 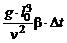
| Мера отношения силы молекулярного трения к подъемной силе, обусловленной различием плотностей жидкости в отдельных точках неизотермического потока. |
| Число Прандтля | Pr | 
| Характеризует влияние физических свойств жидкости на конвективный теплообмен. |
В таблице приняты следующие обозначения:
l 0 - определяющий размер, т.е. характерный линейный размер, оказывающий основное влияние на процесс конвективного теплообмена, м;
w – скорость потока жидкости, м/с;
l - коэффициент теплопроводности среды, Вт/(м×К);
g - ускорение силы тяжести, м/с2;
n - коэффициент кинематической вязкости, м2/с;
b - коэффициент объемного расширения, К-1;
а - коэффициент температуропроводности среды, м2/с.
Число Nu содержит неизвестный коэффициент теплоотдачи a – искомую величину, поэтому является определяемым числом подобия. Зная число Нуссельта, определяют коэффициент теплоотдачи a = Nu×l/ l 0. Числа Pr, Gr и Re – являются определяющими.
Физические параметры, входящие в числа подобия зависят от температуры. Поэтому заранее оговаривается при какой температуре их следует выбирать. Эта температура называется определяющей.
При конвективном теплообмене уравнения подобия могут быть представлены в следующем виде:
Nu = f (Re, Gr, Pr)
Такая зависимость между числами подобия есть следствие второй теоремы теории подобия.
Зависимость между числами подобия в основном определяется опытным путем.
В случае вынужденного движения жидкости и при развитом турбулентном режиме свободная конвекция в сравнении с вынужденной очень мала, поэтому уравнение подобия теплоотдачи упрощается:
Nu = f (Re, Pr).
Для некоторых газов величина числа Прандтля Рг в процессе конвективного теплообмена почти не изменяется с температурой, поэтому уравнение подобия принимает более простой вид:
Nu = f (Re).
При свободном движении жидкости, когда вынужденная конвекция отсутствует, вместо числа Рейнольдса в уравнение подобия необходимо ввести число Грасгофа. Отсюда получаем
Nu = f (Gr, Pr).
Опытное исследование теплоотдачи капельных жидкостей показало, что коэффициент теплоотдачи a будет величиной, различной в условиях нагревания и охлаждения стенки. Это явление связано с изменением физических параметров жидкости в пограничном слое.
Рекомендуется учитывать направление теплового потока соотношением e t = (Рг ж /Рг с)0,25, где Рг ж – число Прандтля при температуре жидкости, а Рг с – число Прандтля при температуре стенки. Тогда общее уравнение подобия для конвективного теплообмена принимает следующий вид:
Nu = с Re n ×Gr b ×Pr m ×e t.
В такой же форме можно представить все уравнения для частных случаев. Количественная связь между числами подобия и является предметом экспериментальных исследований.
Моделирование. Опытное исследование различных физических явлений вообще и тепловых явлений в частности может быть проведено путем непосредственного изучения исследуемого явления на образце или изучения его на модели. Условия, которым должны удовлетворять модель и протекающий в ней процесс, дает теория подобия.
Все подобные друг другу явления некоторой группы представляют собой одно и то же явление, данное в различных масштабах. Следовательно, изучение определенного конкретного явления данной группы равносильно изучению любого другого явления той же группы. Поэтому в тех случаях, когда непосредственное опытное исследование конкретного явления в образце-натуре затруднительно по техническим или экономическим причинам, его заменяют изучением подобного явления в модели.
Моделированием называют метод экспериментального исследования, в котором изучение какого-либо физического явления производится на уменьшенной модели. Идея о моделировании вытекает из того, что всякое явление, описанное в безразмерных переменных, отражает признаки группы подобных явлений.
Для того чтобы модель стала подобна образцу, необходимо выполнить следующие условия. Моделировать можно процессы, имеющие одинаковую физическую природу и описываемые одинаковыми дифференциальными уравнениями. Условия однозначности должны быть одинаковы во всем, кроме численных значений постоянных, содержащихся в этих условиях. Условия однозначности требуют: геометрического подобия образца и модели, подобия условий движения жидкости во входных сечениях образца и модели, подобия физических параметров в сходственных точках образца и модели, подобия температурных полей на границах жидкой среды. Кроме того, одноименные определяющие числа подобия в сходственных сечениях образца и модели должны быть численно одинаковы.
Практически точное осуществление всех условий моделирования выполнить затруднительно. Поэтому была разработана методика приближенного моделирование заключающаяся в стабильности и автомодельности потока и применяющая метод локальности.
Геометрическое подобие образца и модели осуществить нетрудно. Подобное распределение скоростей во входном сечении также может быть выполнено относительно просто. Подобие физических параметров в потоке жидкости для модели и образца выполняется лишь приближенно, а подобие температурных полей у поверхностей нагрева в модели и образце осуществить очень трудно. В связи с этим применяютприближенный метод локального моделирования.
Локальное моделирование заключается в том, что подобие температурных полей осуществляется не во всем объеме аппарата, а в отдельных его местах – сечениях, где производится исследование теплоотдачи. Равенство определяющих критериев в образце и модели может быть выполнено приближенно.
Явление автомодельности заключается в том, что при движении жидкости для довольно широкого диапазона скоростей имеет место почти не меняющееся распределение скорости в данном сечении, т. е. оно практически перестает зависеть от Re.
В настоящее время моделирование является одним из основных методов научного исследования и широко используется во многих областях науки и техники.






