Коэффициент теплоотдачи. Дифференциальные уравнения теплообмена

В процессе конвективного переноса теплоты характер течения жидкости имеет очень большое значение, так как им определяется механизм теплоотдачи. Процесс переноса теплоты на границе с поверхностью канала может быть выражен законом Фурье

dQ = –l dF (dt / dn) _{n = 0},

где п — нормаль к поверхности тела.   

Это же количество теплоты можно выразить уравнением Ньютона-Рихмана

dQ = a dF (t _ж – t _с).

Приравнивая эти уравнения, получим

–l dF (dt / dn) _{n = 0} = aD t,или a= –(l/D t)(dt / dn) _{n = 0}.

Это дифференциальное уравнение описывает процесс теплообме­на на поверхности канала   (п = 0).

По своему физическому характеру конвективный теплообмен яв­ляется сложным процессом и зависит от большого числа фак­торов, определяющих процесс теплоотдачи. Коэффициент теплоотдачи a характеризует интенсивность теплообмена между жидкостью и поверх­ностью канала. В общем случае коэффициент теплоотдачи является функцией физических параметров жидкости, характера течения жид­кости, скорости движения жидкости, формы и размеров тела и др.

Отсюда коэффициент теплоотдачи

a = f (w, l, m, r, с, X, t _ж, t _с, D t, Ф, l ₁, l ₂, l ₃...),

где X – характер движения жидкости (свободное или вынужденное движение);

Ф – форма стенки;

l ₁, l ₂, l ₃ – размеры поверхности.

Уравнение показывает, что коэффициент теплоотдачи – величина сложная и для ее определения невозможно дать общую фор­мулу. Обычно для определения a приходится прибегать к опытным исследованиям.

Применяя общие законы физики, можно составить дифференциаль­ные уравнения для конвективного теплообмена, учитывающие как теп­ловые, так и динамические явления в любом процессе.

Система дифференциальных уравнений состоит из уравнений энер­гии (или теплопроводности), теплообмена, движения и сплошности.

Дифференциальное уравнение энергии ус­танавливает связь между пространственным и временным изменением температуры в любой точке движущейся жидкости:

,

где a = l/(C ×r) – коэффициент температуропроводности;

– оператор Лапласа.                            \.

Если w_x = w_y = w_z = 0, уравнение энергии переходит в уравне­ние теплопроводности для твердых тел (без внутренних источников теплоты).

Дифференциальное уравнение теплооб­мена выражает условия теплообмена на границе твердого тела и жидкости:

a= –(l/D t)(dt / dn) _{n = 0}

Дифференциальное уравнение движения вязкой несжимаемой жидкости представлено уравнением Навье-Стокса:

для оси х

.

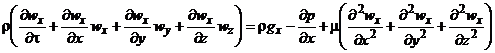Аналогично можно записать уравнения для оси у и оси z.

Это уравнение справедливо для ламинарного и турбулентного движений. В последнем случае w представляет собой действительную (мгновенную) скорость, равную сумме средней и пульсационной скоростей.

Дифференциальное уравнение сплошности или неразрывности, для сжимаемых жидкостей имеет вид

.

Для несжимаемых жидкостей при r = const уравнение сплошности принимает вид

.