При знакомстве младшего школьника на уроке математики с геометрическими фигурами, можно познакомить с одной из самых «необыкновенных» фигур геометрии – Лента Мёбиуса. Тем самым можно расширить кругозор детей, так же дать им возможность развить мышление и логику при создании других фигур из ленты Мёбиуса. (Рис.11.) [6]
Рис.11.
При небольшом «колдовстве» над загадочной поверхностью ленты могут получаться интересные фигуры.
Если разрезать ленту Мебиуса с тремя или большим количествам полуоборотов, то получатся кольца, называющиеся парадромными. (Рис.12.).
Рис.12.
Если склеить вместе две ленты Мебиуса вдоль границ, то выйдет другая удивительная фигура – бутылка Кляйна, но ее нельзя сделать в обычном трехмерном пространстве. (Рис.13.).
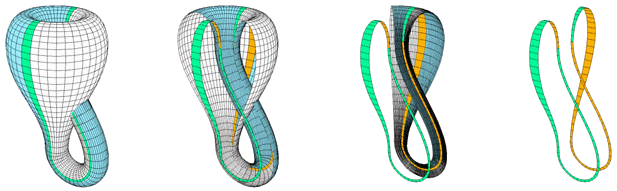
Рис.13.
Если сгладить некоторые грани листа Мебиуса, то выйдет невозможный треугольник Пенроуза. Это плоский треугольник-иллюзия, когда смотришь на него, он кажется объемным. (Рис.14.)
Рис.14.
С развитием информационных технологий деятельность учитель приобрела новую задачу – задачу сделать обучение математике более наглядным. Подвижная наглядность помогает детям лучше понимать, сравнивать и запоминать материал. С ее помощью можно сравнивать геометрические фигуры способом наложения друг на друга (Рис.15.), (Рис.16.), так же наглядность помогает в изучении дробей. [2]
Рис.15.
Рис.16.
Для того чтобы детям было проще понять дроби, можно использовать наглядность в виде презентации с анимациями, где дети смогут увидеть деление целого на части, как они соотносятся между собой, а также они смогут их сравнить. (Рис.17.) (Рис.18.) (Рис.19.).
Рис.17.
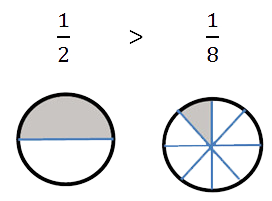
Рис.18.
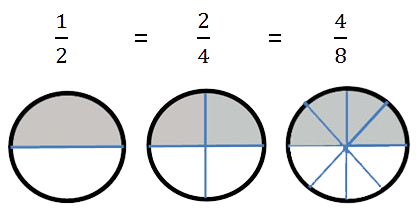
Рис.19.
Заключение
Целью данного исследования было выделить и раскрыть сущность основных направлений развития математики XX века. Было доказано, что особенное развитие математики XX века получили новые области развития такие как: топология, теория случайных процессов, кибернетика и другие. Раскрыв выбранные направления: топология, риманова геометрия, теория вероятности, можно сделать вывод, что развитие математики XX века играет большую роль в развитии математики и геометрии последующих эпох. На данном этапе математика раскрывается глубже, так как ученые уже на имеющихся знаниях строят, развивают и доказывают свои открытия, законы, разработки и т.д. Яркими примерами являются Б.Риман, А.Мёбиус, А.Н. Колмогоров. Развитие математики XX века внесло огромный вклад в развитие современных технологий.
В работе ставились и были решены следующие задачи:
1. Рассмотреть основные направления математики XX века. Рассмотрели направления развития математики, разделили их на две группы.
2. Раскрыть сущность направлений: топология, риманова геометрия, теория вероятности. Были раскрыты данные направления, выделены основные факторы и этапы развития.
3. Рассмотреть новые области применения математики в XX веке. Рассмотрели связь теории вероятности в развитии современных технологий, а также развитие компьютерных технологий в математике.
4. Ознакомиться с использованием сведений о современном развитии математики в начальной школе. Было рассмотрено демонстрирование ленты Мёбиуса на уроках математики, а также использование ИТ на уроках математики.
Таким образом, цель исследования достигнута.
Список литературы
1. Александров П.С. Введение в теорию множеств и общую топологию. М., 1977
2. М.В.Бастриков, О.П.Пономарев. Информационные технологии управления: Учебное пособие. — Калининград: Ин-та «КВШУ», 2005. — 140 с.
3. Бураго Ю. Д., Залгаллер В. А. Введение в риманову геометрию, — СПб: Наука, 1994. 318 с.
4. Вентцель Е. С. Теория вероятностей. — Изд. 4-е, стереотипное. — М.: Наука, 1969. — С. 17. — 577 с
5. Вейль Г. Полвека математики (1900-1950). — М.: Знание, 1969.
6. Гарднер М. Математические чудеса и тайны.— М.: Наука, 1978.
7. Гнеденко Б. В. О работах М. В. Остроградского по теории вероятностей // Историко-математические исследования. — М.: ГИТТЛ, 1951. — № 4. — С. 120.
8. Громол Д., Клингенберг В., Мейер В. Риманова геометрия в целом — М.: Мир, 1971
9. Гурский Д.А. Вычисления в Mathcad. — Мн.: Новое знание, 2003.
10. Колмогоров А. Н. Роль русской науки в развитии теории вероятностей // Учёные записки МГУ. — Μ., 1947. — Т. I, вып. 91, кн.1. — С. 53—64.
11. Колмогоров А. Н., Юшкевич А. П. (ред.). Математика XIX века. — М.: Наука, 1978-1987.
12. Куратовский А. Топология, тт. 1–2. М., 1966, 1969
13. Келли Дж. Общая топология. М., 1981
14. Математические события XX века. Сборник. — М.: ФАЗИС, 2003. — 560 с.
15. Спеньер Э. Алгебраическая топология. М., 1971
