Основные логические операции.

КОНСПЕКТ ЛЕКЦИЙ

по дисциплине

«ФУНКЦИОНАЛЬНАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ»

направления 211000.62

«Конструирование и технология электронных средств»

 

Калуга, 2013

СОДЕРЖАНИЕ

Основы теории множеств…………………………………………………………....………3

Основные логические операции…………………………………………………………….6

Структуры данных………………………………………………………..…………….……9

Основные понятия теории алгоритмов…………………………………….……………...14

Анализ и разработка алгоритмов…………………………………………………………..15

Анализ и разработка алгоритмов. Алгоритмы обработки данных……………………...17

Основные алгоритмы теории графов………………………………………………………22

Алгоритмы решения задач вычислительной математики………………………………...27

Литература…………………………………………………………………………………...32

Основы теории множеств.

Множество — любая совокупность определенных и различимых между собой объектов, рассматриваемых как единое целое. Природа таких объектов может быть совершенно любой. Это могут быть числа, функции, книги, молекулы, высказывания, сами множества.

Существенными в понятии множества являются следующие признаки:

1.      Объекты, входящие во множество, определенные. Это означает, что для каждого объекта можно однозначно сказать, принадлежит ли он данному множеству или нет.

2.      Объекты, входящие во множество, различимы между собой. Следовательно, во множестве не может быть двух или более одинаковых объектов.

3.      Все объекты, входящие во множество, мыслятся как единое целое. Этим подчеркивается, что все объекты рассматриваются в совокупности, а от свойств отдельных объектов абстрагируются.

Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают большими буквами латинского алфавита, его элементы — маленькими. Если x — элемент множества А, то записывают (x принадлежит А). Если x не является элементом множества А, то записывают (x не принадлежит А).

Виды множеств

Пустое множество - множество, не содержащее ни одного элемента. Обозначается символом.

Конечное множество - множество, состоящее из конечного числа элементов. Число элементов в конечном множестве называют его мощностью и обозначают , где А – данное конечное множество.

Бесконечное множество - состоит из бесконечного числа элементов (тоесть элементы у множества пересчитать невозможно).

Способы задания множества

Основных способов задания множества два.

Перечисление состоит в получении полного списка элементов множества.

Описание заключается в задании такого свойства, которым элементы данного множества обладают, а все остальные нет. Чаще всего при этом используют запись A = { x|P(x) }, которую читают следующим образом: "A есть множество элементов x таких, что для них выполняется свойство P(x)".

Например, B = { x| x- натуральное число, меньшее 10 }, при этом, очевидно, B = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }.

Подмножества.

Множество А является подмножеством множества В, если любой элемент, принадлежащий А, также принадлежит В.  Записывается это так  или

Такую ситуацию часто изображают схемотически:

Подобные схемы называют диаграммами Эйлера-Венна.

Из определения следует, что любое множество является своим подмножеством, а также пустое множество является подмножеством любого множества, то есть  и

 

 

Порядковые статистики.

i-й порядковой статистикой множества, состоящего из n элементов будем называть, i-й элемент в порядке возратания. Например, минимум такого множества – это первая порядковая статистика (i = 1), а его максимум – это n-я порядковая статистика. Медиана неформально обозначает середину конечного множества. Если n нечётное, то медиана единственная, и её индекс равен 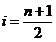; если же n чётное, то медианы две, и их индексы равны  и .

Операции над множествами.

К важнейшим операциям, которые применяются к множествам, относятся:

Объединение: Пусть A и B - множества. Их объединением называется множество, содержащее все элементы, принадлежащие либо множеству A, либо B, либо им обоим. Объединение обозначается через .

А = {1, 2, 3, 4, 5}; B = {2, 3, 10, 11};

={1, 2, 3, 4, 5, 10, 11}

Пересечение множеств  Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В.

А = {1, 2, 3, 4, 5}; B = {2, 3, 10, 11};

={2, 3}.

 

 

    

Разностью множеств А и В 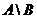называется множество всех тех и только тех элементов А, которые не содержатся в В.

А = {1, 2, 3, 4, 5}; B = {2, 3, 10, 11};

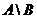={1, 4, 5}.

 

Симметрической разностью множеств А и В 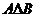называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В

А = {1, 2, 3, 4, 5}; B = {2, 3, 10, 11};

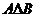={1, 4, 5, 10, 11}.

 

 

Дополнение.

Дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А.

 

Прямое произведение множеств А и В.

А = {a, b, c}; B = {1, 2, 3};

={(a1), (a2), (a3), (b1)…(c3)}.

 

Нечёткие множества.

Пусть E - универсальное множество, x - элемент этого множества, а R - определенное свойство. Обычное (четкое) подмножество A универсального множества E, элементы которого удовлетворяют свойству R, определяется как множество упорядоченной пары A = {mA (х)/х}, где mA(х) - характеристическая функция, принимающая значение 1, когда x удовлетворяет свойству R, и 0 - в другом случае. Нечеткое подмножество отличается от обычного тем, что для элементов x из E нет однозначного ответа "нет" относительно свойства R. В связи с этим, нечеткое подмножество A универсального множества E определяется как множество упорядоченной пары A = {mA(х)/х}, где mA(х) - характеристическая функция принадлежности (или просто функция принадлежности), принимающая значение в некотором упорядоченном множестве M (например, M = [0,1]). Функция принадлежности указывает степень (или уровень) принадлежности элемента x к подмножеству A. Множество M называют множеством принадлежностей. Если M = {0,1}, тогда нечеткое подмножество A может рассматриваться как обычное или четкое множество.

В качестве примера рассмотрим множество X всех чисел от 0 до 10. Определим подмножество A множества X всех действительных чисел от 5 до 8. A = [5,8] Покажем функцию принадлежности множества A, эта функция ставит в соответствие число 1 или 0 каждому элементу в X, в зависимости от того, принадлежит данный элемент подмножеству A или нет. Результат представлен на следующем рисунке:

Можно интерпретировать элементы, соответствующие 1, как элементы, находящиеся в множестве A, а элементы, соответствующие 0, как элементы, не находящиеся в множестве A.

Далее рассмотрим нечёткое множество, например множество молодых людей. Формально можно записать так B = {множество молодых людей}.

Операции над нечёткими множествами:

Пусть A и B - нечеткие множества на универсальном множестве E.

Содержание. Говорят, что A содержится в B, если для x  E mA(x) <mB(x).

Равенство. A и B равны, если для x  E mA(x) = mB (x).

Дополнение. Пусть функция принадлежности лежит в интервале [0,1]. A и B дополняют друг друга, если

Для всех x  E выполняется условие mA(x) = 1 - m B(x).

Пересечение. A|B - наибольшее нечеткое подмножество, которое содержится одновременно в A и B. mA|B(x) = min(mA(x), mB(x)).

Объединение. А И В - наименьшее нечеткое подмножество, которое включает как А, так и В, с функцией принадлежности: mAИ B(x) = max(mA(x), m B(x)).

Разность. А-В. mA-B(x) = min(mA(x), 1 - m B(x)).

 

Основные логические операции.

Основные логические операции:

1. Инверсия (отрицание, НЕ).

Обозначение: .

Таблица истинности для инверсии имеет следующий вид:

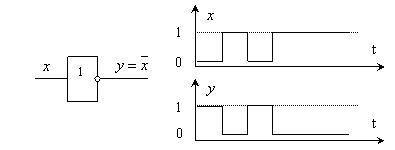
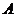
0	1
1	0

 

 

2. Конъюнкция (Логическое умножение, И, AND).

Обозначается символами: , .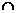

Конъюнкцией n переменных   называется функция, которая принимает значение1, только в том случае, если все переменные равны1 и принимает значение 0 во всех остальных случаях.

Таблица истинности имеет следующий вид:

 

0	0	0
1	0	0
0	1	0
1	1	1

 

 

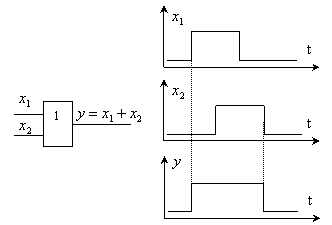
3. Дизъюнкция (Логическое сложение, ИЛИ, OR).

Обозначается символами: , .

Дизъюнкцией n переменных  называется такая функция, которая равна 0 только когда все переменные равны 0 и равна 1 во всех остальных случаях.

Таблица истинности имеет следующий вид:

0	0	0
1	0	1
0	1	1
1	1	1

 

 

4. Исключающее ИЛИ (XOR).

Обозначается символом:  

Таблица истинности имеет следующий вид:

0	0	0
1	0	1
0	1	1
1	1	0