ТЕОРИЯ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Методические указания к выполнению заданий
Омск
Издательство ОмГТУ
2015
Составитель М. В. Силков
Рассматриваются отдельные звенья и системы автоматического регулирования,а также их основные характеристики (временные и частотные). Приведены заданияи примеры их выполнения срасчетами основных характеристик и построением графиков с помощью программы Matlab как для отдельных звеньев, так и для систем автоматического регулирования в целом.
Методические указания будут полезны студентам всех направлений, изучающим курс «Основы автоматического регулирования».
Печатается по решению редакционно-издательского совета
Омского государственного технического университета
© ОмГТУ, 2015
З адание1. Определение основных характеристик
Звеньев САР
Система автоматического регулирования (САР) состоит из отдельных звеньев. Звеном называется любое устройство, входящее в состав САР, например: датчик, усилитель, регулятор, исполнительный элемент, сам объект регулирования. Каждое звено имеет вход х 1 и выход х 2, а также полученное на основе базовых законов дифференциальное уравнение, связывающее х 1 и х 2. Если это уравнение является линейным, то и звено называется линейным, и для него можно получить передаточную функцию, которая есть основа для оценки динамических свойств как самого звена, так и всей САР как совокупности звеньев.
Для получения передаточной функции звена применяется преобразование Лапласа, которое позволяет перейти от дифференциального уравнения звена к соответствующему алгебраическому уравнению. Преобразование Лапласа ставит в соответствие каждой функции времени f (t) функцию F (s), где s – оператор Лапласа (комплексный аргумент):
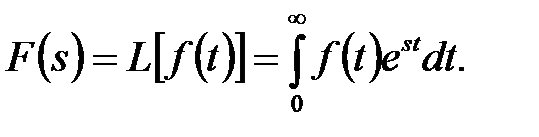 (1)
(1)
Кроме того, используются следующие свойства преобразования Лапласа:
1. Постоянный множитель можно выносить за знак преобразования:
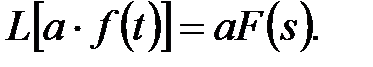 (2)
(2)
2. Преобразование Лапласа от суммы двух функций времени равно сумме их преобразований:
 (3)
(3)
3. Преобразование Лапласа от производной функции времени при нулевых начальных условиях и от её интеграла находится по следующим формулам:
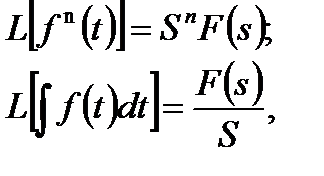 (4)
(4)
где n – степень производной.
Приведём ниже пример преобразования Лапласа для линейного дифференциального уравнения второго порядка, описывающего динамику какого-то звена. В нём постоянные коэффициенты a, b, c, d, e зависят от реальных физических характеристик звена, например от массогабаритных характеристик, жёсткостей пружин, коэффициентов демпфирования, теплоёмкости, теплопроводности, электрических сопротивлений, ёмкостей, индуктивностей и т.д. в зависимости от конкретного звена:
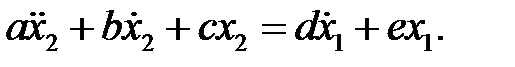 (5)
(5)
После применения свойств преобразования Лапласа, описанных выше, переходим от функций времени х 1 и х 2 к функциям от s:
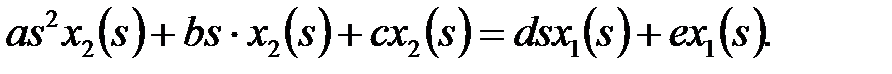 (6)
(6)
Передаточной функцией звена называется отношение преобразований Лапласа выходной величины звена к входной, т.е.
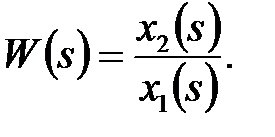 (7)
(7)
Из выражения (6) легко получить это отношение:
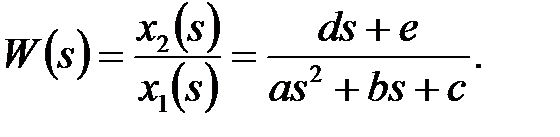 (8)
(8)
В передаточной функции свободные члены полиномов числителя и знаменателя должны быть равны единице. Для этого в (8) выносим в числителе за скобки e, a в знаменателе – c:
 (9)
(9)
где 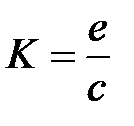 – коэффициент передачи звена;
– коэффициент передачи звена;
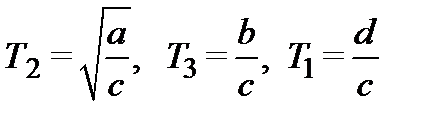 – постоянные времени звена, размерность которых – секунда.
– постоянные времени звена, размерность которых – секунда.
Коэффициент передачи характеризует отношение выхода ко входу
в статике, т.е. в установившемся режиме звена, когда закончился переходный процесс и на входе и выходе установятся постоянные значения х 10
и х 20. Например, если звено является датчиком координаты и преобразует значение координаты х 10 в пропорциональное значение напряжения на выходе звена х 20, то при К = 5 В/ммкаждому изменению входной координаты на 1 мм будет соответствовать изменение выходного напряжения на 5В.
Постоянные времени характеризуют длительность переходного процесса (чем они больше, тем больше времени занимает переходной процесс). Вид же переходного процесса зависит от вида и порядка полиномов числителя и знаменателя W (s). Для звеньев не старше второго порядка вид переходного процесса легко получить аналитически как результат решения уравнения (5).Они хорошо изучены, и в литературе можно найти эти выражения и графики переходного процесса. На рис. 1 представлены примеры двух видов переходных процессов, полученных при подаче на вход звена единичного ступенчатого сигнала.
| Х21 |
| Х22 |
| Х2 |
| Х1 |
| К |
| Х1 |
| t |
| 1 |
Рис. 1. Переходные процессы для двух звеньев:
х 21 – для 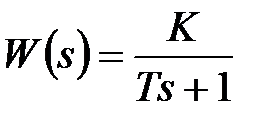 ; х 22 – для
; х 22 – для 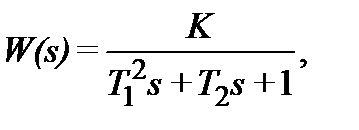 где Т 2á 2 Т 1
где Т 2á 2 Т 1
Рассмотрим далее получение передаточных функций, связывающих вход – ток и выход – напряжение для простейших участков электрической цепи.
1. Для активного сопротивления R напряжение и ток связаны законом Ома U = RI или, переходя к функциям от s, получим U (s) = RI (s). Тогда 
2. Для участка цепи с индуктивным сопротивлением L можно записать 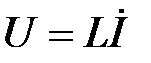 или
или 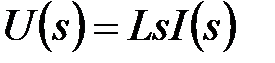 . Тогда
. Тогда 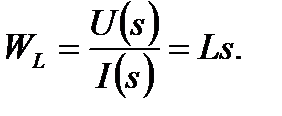
3. Для участка цепи с конденсатором ёмкостью С получим  или
или 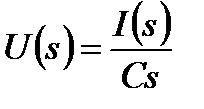 . Тогда
. Тогда 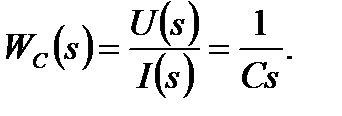
Используя только что полученные выражения для передаточных функций, или что тоже самое для сопротивлений простых участков цепи, можно определять, например, передаточные функции операционных усилителей, применяемых в системах регулирования. Схема одного из усилителей приведена на рис. 2. Известно, что передаточная функция операционного усилителя находится по формуле
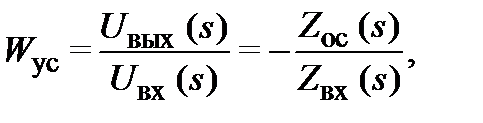 (10)
(10)
гдеZвых(s),Zос (s)– сопротивления входной цепи и цепи обратной связи. Последние зависят от того, какие элементы (R, С) включены в них и как они соединены (последовательно или параллельно).
Для усилителя (рис. 2) имеем на входе последовательное соединение звеньев, поэтому 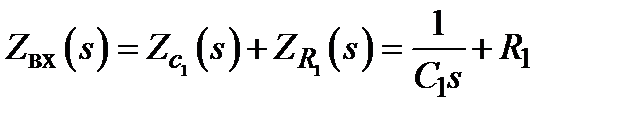 . В обратной связи имеем параллельное соединение, тогда
. В обратной связи имеем параллельное соединение, тогда
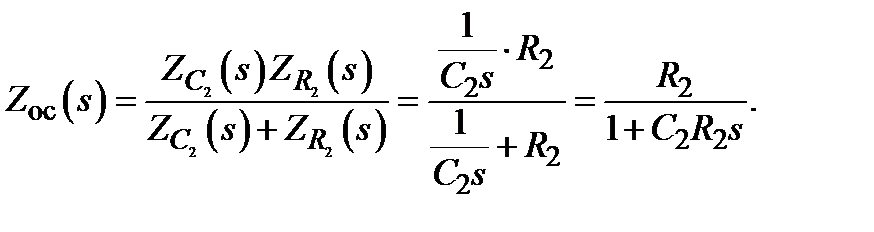
В итоге получим передаточную функцию усилителя
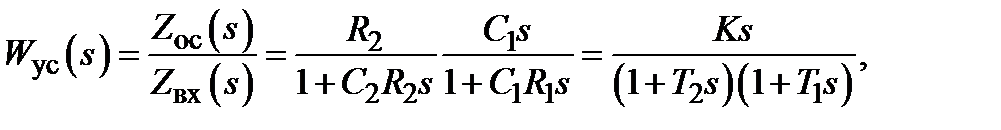 (11)
(11)
где 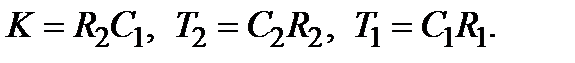
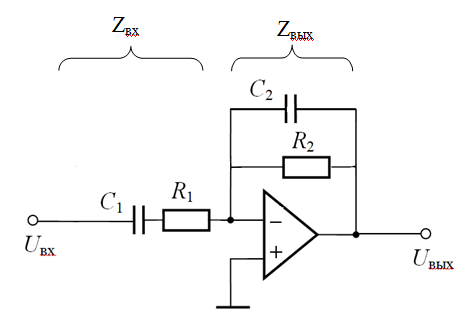
Рис. 2. Операционный усилитель
Зная передаточную функцию звена, можно определить его переходную характеристику, т.е. реакцию звена (переходный процесс и установившееся значение выхода) на поданный на его вход единичный ступенчатый сигнал. Для этого можно использовать программу Matlab. После запуска программы необходимо нажать кнопку «Новое окно», после чего откроется окно редактора программ. В нём можно создать простую программу для составления передаточной функции звена, построения его переходной характеристики и частотных характеристик. Пример этой программы с необходимыми комментариями (они начинаются знаком %)приведён ниже (пример соответствует заданию 2, для задания 1 программа проще и составляется по аналогии).
%Построение временных и частотных характеристик звеньев и систем %регулирования
s=zpk('s');%задание переменной Лапласа
'передаточная функция звена 1'
W1=2*(0.02*s+1)/(0.5*s+1)
'передаточная функция звена 2'
W2=2/(0.2*s+1)
'передаточная функция звена 3'
W3=1/(0.08*s+1)
'передаточная функция разомкн. сист.при послед.соедин. трех звеньев'
Wraz=W1*W2*W3
'передаточная функция разомкн. сист. в виде дроби с полиномами от "s" 'Wraz_pol=tf(Wraz)
'передаточная функция замкн. сист. при единичной обратной связи'
Wzam= feedback(Wraz_pol,1,-1)
%Построение необходимых графиков
figure(1)%задание первого окна графика
nyquist(Wraz)%построение графика АФХ разомкнутой системы
figure(2)
bode(Wraz),grid%построение графиков ЛАХ и ЛФХ разомкн. сист. и сетки на %графиках
figure(3)
pzmap(Wzam)%карта нулей(корней числителя) и полюсов (корней знаменателя)
%передат. функции замкнутой системы
figure(4)
step(Wzam),grid%построение графика переходной характеристики замкнутой %системы
figure(5)
Для выполнения программы необходимо нажать кнопку «RUN» в панели инструментов вверху окна. Восновном командном окне программа выведет выражения для всех необходимых передаточных функций. Кроме того, в отдельных окнах будут построены необходимые графики с сеткой. После чего для каждого графика правой кнопкой мыши можно вызвать контекстное меню и получить основные характеристики по графику. Например, для переходной характеристики это установившееся значение выхода х 20, время регулирования t п и перерегулирование s. Здесь время регулирования – это время окончания переходного процесса. Оно принимается как время вхождения выходной величины в коридор шириной ±2% от х 20. Перерегулирование s- это максимальное отклонение от х 20,выраженное в процентах  .
.
Рассмотрим далее методику и физический смысл построения частотных характеристик. При пропускании через линейное звено гармонического сигнала 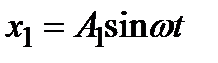 частота на выходе не изменяется, но меняется амплитуда и появляется фазовый сдвиг j, т.е.
частота на выходе не изменяется, но меняется амплитуда и появляется фазовый сдвиг j, т.е.  . Как меняется отношение амплитуд
. Как меняется отношение амплитуд 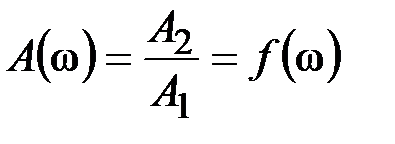 и фазовый сдвиг
и фазовый сдвиг  в зависимости от частоты сигнала w, и показывают частотные характеристики звена. Для построения соответствующих графиков сначала определяется частотная передаточная функция звена
в зависимости от частоты сигнала w, и показывают частотные характеристики звена. Для построения соответствующих графиков сначала определяется частотная передаточная функция звена 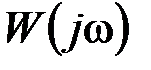 , которая получается из основной передаточной функции W (s) заменой s на w j. Полученную комплексную функцию приводят далее к экспонентной форме записи. Для этого каждый комплексный сомножитель
, которая получается из основной передаточной функции W (s) заменой s на w j. Полученную комплексную функцию приводят далее к экспонентной форме записи. Для этого каждый комплексный сомножитель 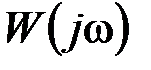 приводят к этой форме,например сомножитель вида
приводят к этой форме,например сомножитель вида 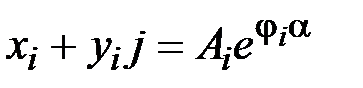 ,где
,где 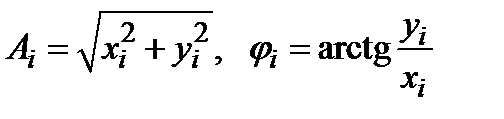 . Последние формулы следуют из графической интерпретации комплексного числа в виде точки на комплексной плоскости с координатами xi, yi.
. Последние формулы следуют из графической интерпретации комплексного числа в виде точки на комплексной плоскости с координатами xi, yi.
К ней можно из начала координат провести вектор с модулем Ai и углом поворота j i (угол отсчитывают от оси Х против часовой стрелки со знаком «+» и по часовой – «-») (рис. 3).
| Xi |
| Yi |
| Ai |
| j i |
Рис. 3. Графическая интерпретация комплексного числа
Для полученной в примере передаточной функции (11) частотная передаточная функция будет иметь вид
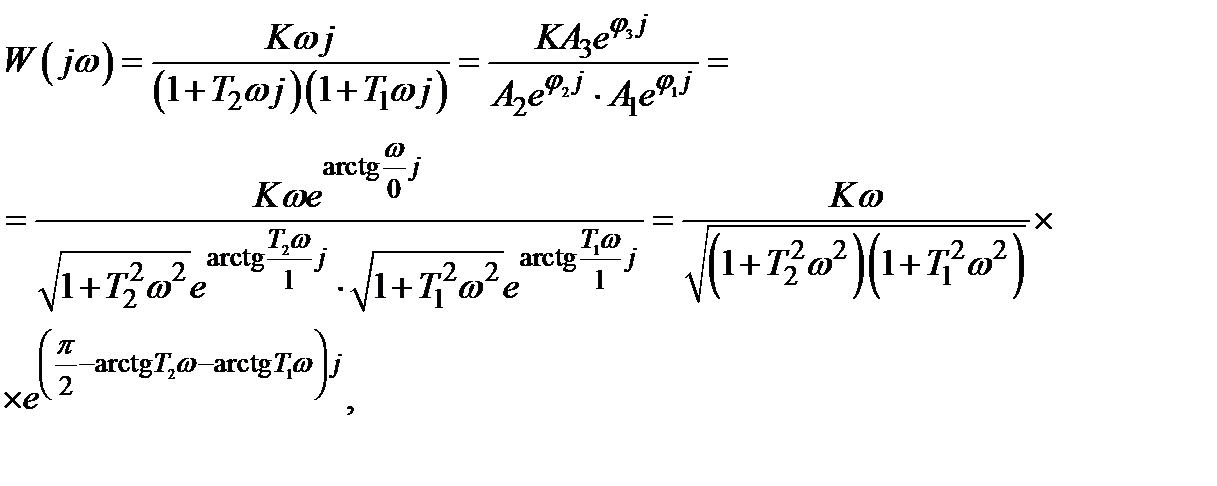 (12)
(12)
где 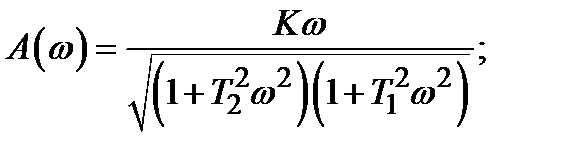
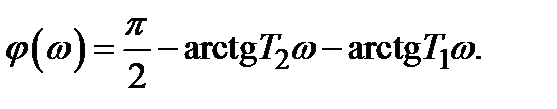
График, построенный на комплексной плоскости как совокупность точек концов вектора А (w) при его повороте на угол j(w) при изменении w от 0 до ¥, называется амплитудно-фазочастотной характеристикой (АФХ) звена. При определённой частоте w0 получаем на графике точку, к которой можно провести вектор с А (w0) и j(w0). Первое значение покажет отношение амплитуд выхода ко входу  , а второе – фазовый сдвиг выходного гармонического сигнала по отношению ко входному
, а второе – фазовый сдвиг выходного гармонического сигнала по отношению ко входному 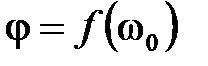 .
.
Кроме того, можно построить отдельные два графика А= f (w) и j =
= f (w). Они называются амплитудно- и фазочастотными характеристиками (АЧХ) и (ФЧХ). Но более распространены в теории регулирования их аналоги–логарифмические амплитудная и фазовая характеристики (ЛАХ) и (ЛФХ). Они отличаются от предыдущих тем, что по оси частот используется логарифмический масштаб. То есть риски на горизонтальной оси наносятся согласно выражению lgw, а возле каждой риски проставляется значение самой частоты w. Это позволяет при небольшой длине оси показать большие изменения w, так какlg10 = 1, lg100 = 2 и т.д. Интервал изменения частоты в 10 раз называется декадой. Кроме того, на графике ЛАХ по вертикальной оси откладывают не А (w), а L (w) = 20lg А (w). Единицы измерения L (w) – децибелы. Например L (w) = 20Дб соответствует А (w) = 10, что показывает увеличение амплитуды выхода в 10 раз при прохождении сигнала через звено на данной частоте. Если L (w) = –20Дб, то А (w) = 0,1, т.е. амплитудавыхода уменьшаетсяв 10 раз.
Графики АФХ, ЛАХ и ЛФХ легко строятся с помощью команд Matlab, приведённых в программе выше. При этом следует отметить следующие особенности построения ЛАХ и ЛФХ. Если  , то на частотеw = 1 ЛАХ всегда имеет значение L (1) = 20lg К. Через эту точку проходит прямая с наклоном 20×nДб/дек, где n– степень множителя s в W (s) (n= –1, n= 0 или n=1). Наклон участков ЛАХ изменяется вблизи сопрягающих частот
, то на частотеw = 1 ЛАХ всегда имеет значение L (1) = 20lg К. Через эту точку проходит прямая с наклоном 20×nДб/дек, где n– степень множителя s в W (s) (n= –1, n= 0 или n=1). Наклон участков ЛАХ изменяется вблизи сопрягающих частот 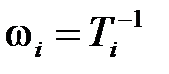 . Наклон изменяется вверх, если Т i находится в числителе W (s), и вниз, если в знаменателе. Он меняется на 20 Дб/дек, если Т i присутствует в сомножителе Т i s +1, и на 40 Дб/дек, если в сомножителе второго порядка
. Наклон изменяется вверх, если Т i находится в числителе W (s), и вниз, если в знаменателе. Он меняется на 20 Дб/дек, если Т i присутствует в сомножителе Т i s +1, и на 40 Дб/дек, если в сомножителе второго порядка 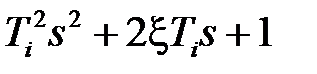 . При этом практически любую передаточную функцию звена или разомкнутой САР можно представить в виде
. При этом практически любую передаточную функцию звена или разомкнутой САР можно представить в виде
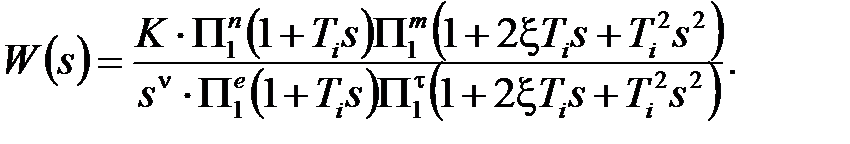 (13)
(13)
В задании 1 необходимо сделать следующее:
1. По заданным схемам операционных усилителей определить их передаточные функции, а затем общую передаточную функцию W (s) звена из трёх последовательно соединённых усилителей.
2. Получить общую частотную передаточную функцию и выражения для А (w) и j(w).
3. Построить график переходной характеристики с помощью программы Matlabи определить по нему время регулирования и перерегулирование для W (s), если оно соответствует пропорциональному звену. Если W (s) соответствует интегральному или дифференциальному звену, то исключить из W (s) множитель s из знаменателя или числителя и также построить переходную характеристику и найти tp и s.
4. Построить АФХ, ЛАХ и ЛФХ для W (s) с помощью программы Matlab.Нанести на график сопрягающие частоты и углы наклона участков ЛАХ. Уметь объяснить вид ЛАХ и ЛФХ в зависимости от вида исходной передаточной функции W (s). Схемы операционных усилителей в зависимости от номера варианта задания приведены в табл. 1 и 2.
Таблица 1
| Вариант | Номера звеньев из табл. 2 | ||
| 1 | 1 | 3 | 5 |
| 2 | 1 | 4 | 6 |
| 3 | 1 | 5 | 4 |
| 4 | 1 | 2 | 8 |
| 5 | 2 | 4 | 5 |
| 6 | 1 | 7 | 4 |
| 7 | 1 | 7 | 3 |
| 8 | 7 | 2 | 1 |
| 9 | 7 | 4 | 8 |
| 10 | 1 | 2 | 9 |
| 11 | 1 | 5 | 1 |
| 12 | 3 | 1 | 5 |
| 13 | 1 | 7 | 1 |
| 14 | 1 | 9 | 1 |
| 15 | 1 | 6 | 2 |
| 16 | 6 | 3 | 1 |
| 17 | 9 | 1 | 1 |
| 18 | 1 | 4 | 2 |
| 19 | 1 | 3 | 6 |
| 20 | 1 | 2 | 7 |
| 21 | 6 | 1 | 4 |
| 22 | 1 | 7 | 8 |
| 23 | 7 | 2 | 2 |
| 24 | 2 | 1 | 2 |
| 25 | 1 | 4 | 3 |
Таблица 2
| № | Электронная модель усилителя* |
| 1 | 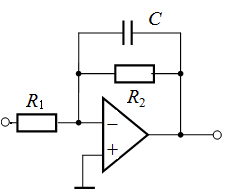
|
| 2 | 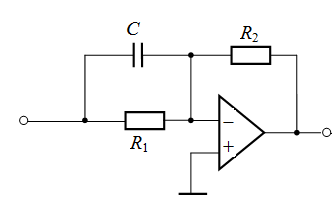 А А
|
| 3 |  Ф Ф
|
Продолжение табл. 2
| 4 | 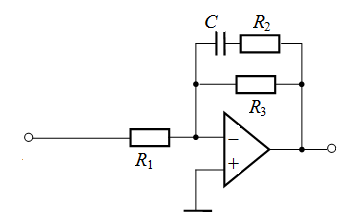 ДИ ДИ
|
| 5 |  ИР ИР
|
| 6 | 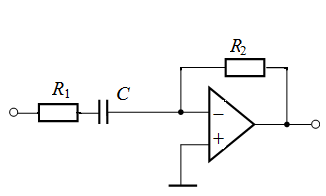 ДA ДA
|
Окончание табл. 2
| 7 | 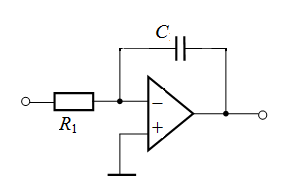 И И
|
| 8 | 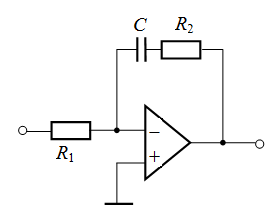 ПИ ПИ
|
| 9 | 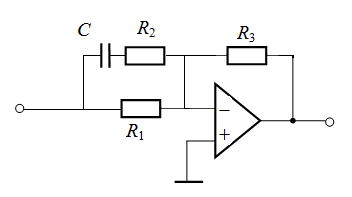 ПИД ПИД
|
* Значение общего коэффициента передачи трёх звеньев принять исходя из выражения К = 30+5 n, где n – номер варианта.Значение наибольшей постоянной времени звеньев принять  Значения остальных постоянных времени определить по формуле
Значения остальных постоянных времени определить по формуле 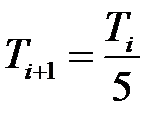 .
.
Контрольные вопросы к заданию 1
1. Какие три основных типа звеньев применяются в САР?
2. Перечислить типовые пропорциональные звенья, их передаточные функции и указать их основные особенности и отличия от интегральных и дифференциальных звеньев.
3. Как получается передаточная функция звена?
4. Показать физический смысл и указать размерность коэффициента передачи звена и постоянной времени.
5. Что такое переходная характеристика звена и какие показатели качества САР по ней можно определить?
6. Как можно вручную построить на комплексной плоскости АФХ, взяв за основу передаточную функцию звена?
7. Рассказать алгоритм построения ЛАХ и ЛФХ, отталкиваясь от передаточной функции звена.
8. Показать связь между видом передаточной функции и видом ЛАХ.
З адание2. Анализ и синтез САР
Задание 2 посвящено анализу системы автоматического регулирования (САР) по заданной для него передаточной функции. В этом случае сначала определяют передаточную функцию разомкнутой W р(s) и замкнутой W 3(s) САР. Разомкнутую САР получают условно, разомкнув главную обратную связь перед сумматором. Для получения этих передаточных функций в задании 2 можно использовать следующие три простых правила упрощения структурных схем.
1. При последовательном соединении звеньев их передаточные функции перемножаются для получения передаточной функции эквивалентного звена.
2. При параллельном соединении звеньев их передаточные функции складываются.
3. Звено с передаточной функцией W п(s), охваченное отрицательной обратной связью со звеном W 0(s), может быть заменено эквивалентным звеном W э(s):
 (14)
(14)
После получения W р(s) легко найти характеристическое уравнение для замкнутой САР. Для этого нужно приравнять к нулю знаменатель передаточной функции замкнутой САР:
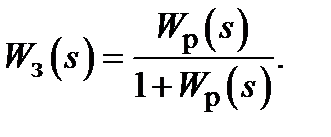 (15)
(15)
По корням характеристического уравнения можно определить устойчивость замкнутой САР. Для устойчивости необходимо и достаточно, чтобы действительные части всех корней уравнения были отрицательными. Расположение корней на комплексной плоскости можно получить
с помощью соответствующего оператора Matlab, приведённого в программе выше. Для этого нужно использовать этот оператор с передаточной функцией W з(s).
Характеристическое уравнение может быть использовано для оценки устойчивости по критерию Гурвица и выбора соответствующего коэффициента передачи разомкнутой САР (К). Рассмотрим пример.
Пусть
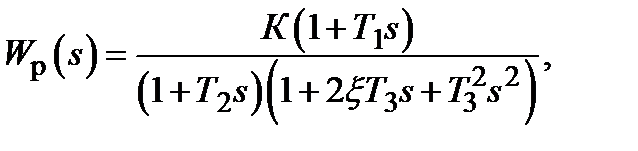 (16)
(16)
тогда характеристическое уравнение запишем в виде
 (17)
(17)
Его можно привести к виду
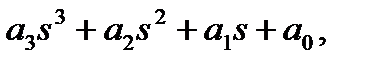
где 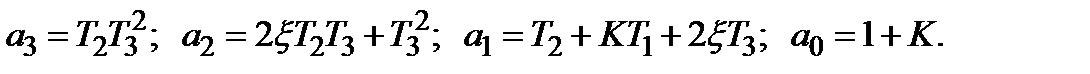
Согласно критерию Гурвица для уравнения третьего порядка для устойчивости САР необходимо, чтобы все коэффициенты а 0, а 1, а 2, а 3были больше нуля и дополнительно выполнялось неравенство
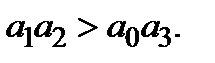 (18)
(18)
Заменив в (18) знак неравенства на равенство, можно найти значение К гр, соответствующее границе устойчивости. Чтобы обеспечить запас устойчивости в 6Дб, необходимо уменьшить это значение в 2 раза.
Оценку устойчивости САР можно провести и по критерию Найквиста по ЛАХ и ЛФХ разомкнутой САР. В этом случае, применяя Matlab, строят эти характеристики и с помощью контекстного меню, вызываемого щелчком правой кнопки мыши на графике, находят запасы устойчивости по амплитуде L 3 и фазе j3(для этого используется пункт меню «характеристики и запасы устойчивости»). Запас по амплитуде находится на частоте wp, соответствующейj=–180° на ЛФХ. Он равен ординате ЛАХ на этой частоте, взятой по модулю (для устойчивости САР эта ордината должна быть отрицательной). Запас по фазе находится на частоте среза wср, соответствующей нулю децибел на ЛАХ. На ЛФХ на этой частоте определяют угол j(wср) < 180°,тогда j3 = 180°–j(wср) (Matlab показывает L 3 и j3 на графике вертикальными линиями и определяет их значения, которые выводятся в окне графика).
Для оценки точности можно определить статическую или скоростную ошибку САР.
САР является статической, если W р(s) имеет вид пропорционального звена (сомножитель s n в знаменателе (13) отсутствует). САР является астатической, если W р(s) имеет вид интегрального звена (множитель s в знаменателе). Для статической САР характерна постоянная установившаяся ошибка
 (19)
(19)
получаемая при подаче на вход САР постоянного задающего сигнала.
В астатической САР при подаче постоянного сигнала x ст = 0, но при подаче линейно меняющегося во времени задающего сигнала (режим слежения с постоянной скоростью)на выходе возникает скоростная ошибка
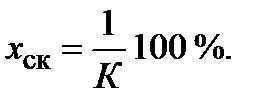 (20)
(20)
Имеющуюся САР можно улучшить, применив коррекцию по методу технического оптимума. Этот метод хорошо зарекомендовал себя для несложных САР с единичной обратной связью. В этом случае передаточную функцию разомкнутой САР нужно привести к виду
 (21)
(21)
где Т m– наименьшая из постоянных времени исходной нескорректированной САР.
Тогда в замкнутом виде система превращается в колебательное звено сx = 0,7, что даёт возможность получить оптимальный по времени переходный процесс для такого звена и малое перерегулирование с s< 5%.
Корректирующее звено, переводящее исходную разомкнутую САР
к виду (21), определяется следующим образом:
 (22)
(22)
Возьмём для примера передаточную функцию разомкнутой САР вида
 (23)
(23)
Пусть Т m = Т 1, тогда из (22) находим
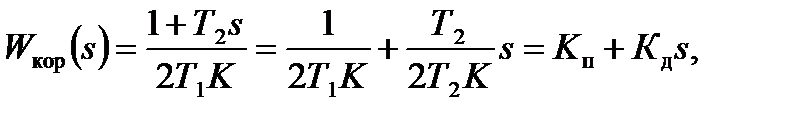 (24)
(24)
т.е. в качестве корректирующего звена можно использовать пропорционально-дифференциальный регулятор.
Другим способом выбора корректирующего звена при последовательной коррекции является использование ЛАХ и ЛФХ разомкнутой САР. В этом случае в одних осях строятся действительная и желаемая ЛАХ. Последняя строится в виде ломаной линии, состоящей из отрезков с наклонами,кратными 20 Дб/дек. Основой для построения желаемой ЛАХ являются требования, предъявляемые к САР по точности, качеству и запасам устойчивости. При построении желаемая ЛАХ делится на три участка: низкочастотный, среднечастотный и высокочастотный.
Низкочастотная часть желаемой ЛАХ выбирается по требованиям точности. По заданному порядку астатизма САР и заданным в процентах величинам статической х ст или скоростной х ск ошибке САР определяется коэффициент передачи разомкнутой САР. Для этого используются формулы
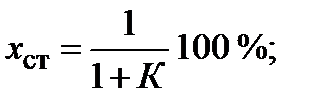
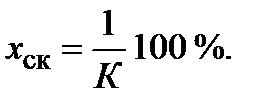 (25)
(25)
При этом надо иметь в виду, что статическая САР не имеет в передаточной функции разомкнутой САР множителя s в знаменателе, а у астатической он есть. После выбора по выражениям (25) желаемого коэффициента К ж можно определить ординату начальной точки низкочастотной желаемой ЛАХ. Она имеет ординату L (1) = 20lg K ж на частоте w = 1. Таким образом, в исходной передаточной функции изменяется коэффициент К до нового значения К жи действительная ЛАХ смещается параллельно самой себе, чтобы её начальная точка при w = 1 совпала с найденным по (25) значением. Наклон желаемой ЛАХ, проходящей через эту точку, равен
–20 Дб/дек,если САР должна быть астатической, или равен нулю, если она должна быть статической.
Среднечастотная часть желаемой ЛАХ определяется требованием по качеству САР. Она представляет собой линию с наклоном –20 Дб/дек, чтобы обеспечить перерегулирование не более 30%. Ширина этого участка 1¸1,5 декады, и в средней части эта линия должна пересекать ось частот при w = wср, где wср называется частотой среза САР. Между ней
и временем регулирования t р существует связь, которую можно приближённо показать выражением
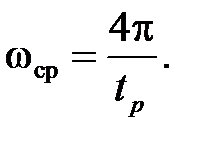 (26)
(26)
Иногда более точно связь этих переменных можно найти с использованием экспериментальных графиков, учитывающих заданное значение перерегулирования s. Но в задании можно использовать выражение (26), чтобы по заданному значению t р определить wср.
Высокочастотная часть желаемой ЛАХ мало влияет на динамику системы, поэтому она либо совмещается с действительной высокочастотной частью ЛАХ, либо идёт ей параллельно. Все три части совмещаются между собой либо непосредственно, либо дополнительными прямыми с наклонами, кратными 20 Дб/дек.
После построения действительной и желаемой ЛАХ (действительная строится с использованием Matlab, а желаемая на этом же графике выполняется карандашом вручную) можно определить ЛАХ корректирующего звена. Для этого надо сначала действительную ЛАХ заменить отрезками ломаной линии с наклонами, кратными 20 Дб/дек (выполнить карандашом). Затем разбить ось частот на участки, где наклоны обеих ЛАХ не меняются. После этого из желаемой ЛАХ надо графически вычесть действительную. Например, если наклон желаемой ЛАХ на участке –20 Дб/дек, а действительной– (–40) Дб/дек, то для ЛАХ корректирующего звена на этом участке получим наклон (–20Дб/дек – (–40 Дб/дек)) = +20 Дб/дек. По полученной ЛАХ корректирующего звена можно определить его передаточную функцию W k(s). При этом надо учитывать следующее. Точки излома линии ЛАХ корректирующего звена определяются сопрягающими частотами w к i и задают постоянные времени Wk (s), т.е. 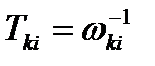 . Далее если после точки излома с данной частотой w ki ЛАХ идёт вверх с наклоном +20 Дб/дек, то в W k(s) в числителе дроби появляется сомножитель (1+T kis). Если же ЛАХ идёт вниз на 20 Дб/дек, то такой же сомножитель появляется в знаменателе W k(s). Если наклон меняется на ±40 Дб/дек, то
. Далее если после точки излома с данной частотой w ki ЛАХ идёт вверх с наклоном +20 Дб/дек, то в W k(s) в числителе дроби появляется сомножитель (1+T kis). Если же ЛАХ идёт вниз на 20 Дб/дек, то такой же сомножитель появляется в знаменателе W k(s). Если наклон меняется на ±40 Дб/дек, то
в числителе или знаменателе появляется сомножитель 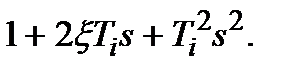
В качестве примера рассмотрим коррекцию САР с передаточной функцией разомкнутой части вида
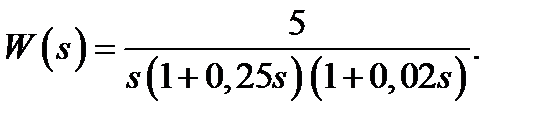 (27)
(27)
Необходимо обеспечить для данной САР следующие характеристики: х ск£ 5%, s < 30% иуменьшить время регулирования t р в 1,5 раза. На рис. 4 сплошной линией показана действительная ЛАХ, совмещенная в низкочастотной части с желаемой, так как из (25) К ж= 20, а не 5, как в (27). Здесь же пунктирной линией показана желаемая ЛАХ, для которой из (26)  , так как
, так как 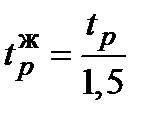 . Разностная ЛАХ корректирующего звена показана жирной сплошной линией. А по ней определена передаточная функция корректирующего звена
. Разностная ЛАХ корректирующего звена показана жирной сплошной линией. А по ней определена передаточная функция корректирующего звена 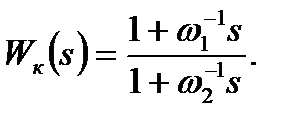 После этого передаточная функция скорректированной ЛАХ примет вид
После этого передаточная функция скорректированной ЛАХ примет вид

Для неё с помощью Matlab необходимо построить ЛАХ и ЛФХ. По ним определить запасы устойчивости по амплитуде L 3и фазе j3 и сравнить их со значениями для нескорректированной САР. Они не должны значительно уменьшиться.
| 20lgK |
| LK |
| w |
| 1 2 4 6 8 10 20 40 60 80 100 |
| wcр |
| L(w) |
| 26 20 |
| Lж |
| Lд |
| w2 |
| w1 |
| wжcр |
Рис.4. Выбор корректирующего звена путём вычитания
из желаемой ЛАХ (L ж) действительной (L д)
На рис.4 приведён один из возможных вариантов выбора корректирующего звена. Возможны и другие варианты, если L ж будет несколько другой. Обычно, чем выше требования кСАР, тем более сложной является W к(s) и её непросто реализовать. Поэтому выбор корректирующего звена всегда связан с компромиссом между его сложностью и более высокими требованиями, предъявляемыми к САР.
Таким образом, в задании 2 нужно сделать следующее:
1. По заданным передаточным функциям звеньев и структурной схеме САР определить передаточные функции разомкнутой W р(s) и замкнутой W з(s) системы (с использованием Matlab).
2. Произвольно задаться коэффициентом К, определить характеристическое уравнение САР и его корни (с использованием Matlab). Сделать заключение об устойчивости САР.
3. Применить критерий Гурвица и найти новое значение К, соответствующее запасу устойчивости в 6Дб.
4. Построить ЛАХ и ЛФХ разомкнутой САР и по критерию Найквиста найти запасы устойчивости по амплитуде и фазе (с использованием Matlab).
5. Определить, является ли САР статической или астатической, и найти значения постоянных установившихся ошибок в процентах.
6. Определить передаточную функцию корректирующего звена по методу технического оптимума. Для скорректированной САР построить переходную характеристику, по ней найти время регулирования t р и перерегулирование s (с использованием Matlab).
7. Выбрать корректирующее звено для САР вторым способом с помощью действительной и желаемой ЛАХ (с использованием Matlab). Требования к желаемой ЛАХ принять следующие. Для статических САР
х ст£ 5%, для астатических САР х ск£ 5%. Перерегулирование s < 30%. Уменьшить время регулирования в 1,5 раза. Запасы устойчивости по амплитуде L 3³ 6 Дб, по фазе j3³ 20°.
Структурная схема исследуемой САР показана на рис.5. Передаточные функции в зависимости от варианта приведены в табл. 3 и 4.
| W1 |
| W2 |
| W3 |
| q |
| y |
Рис.5. Структурная схема САР
Таблица 3
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| № звеньевW1, W2, W3САР из табл.4 | 1 | 1 | 3 | 3 | 1 | 2 | 1 | 1 | 2 | 2 | 3 | 4 | 1 | 5 | 2 | 2 | 2 | 1 | 3 | 1 | 5 | 6 | 5 |
| 1 | 2 | 1 | 2 | 2 | 4 | 3 | 3 | 5 | 6 | 5 | 2 | 3 | 3 | 1 | 3 | 1 | 4 | 1 | 6 | 2 | 2 | 1 | |
| 1 | – | 1 | – | 4 | 3 | 5 | 6 | – | – | 6 | 1 | 1 | 6 | – | – | – | 2 | 5 | 3 | – | – | 6 |
Таблица 4
| Номер звена | Передаточная функция звена* |
| 1 | 
|
| 2 | 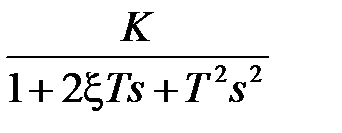
|
| 3 | 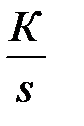
|
| 4 | 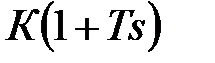
|
| 5 | 
|
| 6 | 
|
* Значение x принять 0,4. Значение наибольшей постоянной времени принять 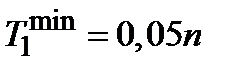 , где n– номер варианта. Значения остальных постоянных времени (включая Т¢ звеньев 5 и 6) определить по формуле
, где n– номер варианта. Значения остальных постоянных времени (включая Т¢ звеньев 5 и 6) определить по формуле  .
.
Контрольные вопросы к заданию 2
1. Какие методы упрощения структурной схемы применяются при получении передаточных функций разомкнутой и замкнутой САР?
2. Как получить характеристическое уравнение САР?
3. Какие корни должны быть у характеристического уравнения устойчивой САР?
4. Как применить для оценки устойчивости критерий Гурвица?
5. Как оценить устойчивость и найти запасы устойчивости по критерию Найквиста для ЛАХ и ЛФХ?
6. Что такое статическая и астатическая САР? Какие они имеют постоянные установившиеся ошибки при постоянном и линейно изменяющемся входных сигналах?
7. Что такое коррекция САР?Для чего она применяется?Виды коррекции.
8. В чём суть последовательной коррекции по методу технического оптимума?
9. Как осуществляют выбор корректирующего звена по действительной и желаемой ЛАХ?
10. Как строится желаемая ЛАХ в зависимости от требований, предъявляемых к САР?Какие она содержит участки?
11. Как по ЛАХ корректирующего звена перейти к его передаточной функции?
Список рекомендуемой литературы
1. Бурьян, Ю.А. Теория автоматического управления (линейные системы):учеб.пособие / Ю.А. Бурьян, М.В. Силков, Д.Н. Ситников. –Омск:Изд-во ОмГТУ, 2005. – 72с.
2. Щукин, О.С. Основы теории линейных системавтоматического управления: учеб.пособие. –Омск: Изд-во ОмГТУ, 2001. – 142с.
3. Аверьянов, Г.С. Управление в технических системах: учеб.пособие / Г.С. Аверьянов, А.Г. Туровец, А.Б. Яковлев. – Омск: Изд-во ОмГТУ, 2005. – 148 с.
4. Попов, Е.П.Теория линейных систем автоматического регулирования и управления / Е.П. Попов. – М.:Наука, 1989. – 352 с.
5. Бессекерский, В.А. Теория систем автоматического регулирования / В.А.Бессекерский, Е.П.Попов. – М.: Наука, 1975. – 768 с.
Оглавление
Задание1. Определение основных характеристик звеньев САР................... 3
Задание2. Анализ и синтез САР..................................................................... 16
Список рекомендуемой литературы.............................................................. 27
Редактор К. В. Муковоз
Компьютерная верстка Ю. П. Шелехиной
Сводный темплан 2015 г.
Подписано в печать 13.03.15. Формат 60×841/16. Отпечатано на дупликаторе.
Бумага офсетная. Усл. печ. л. 1,75. Уч.-изд. л. 1,75.
Тираж 50 экз. Заказ 156.
Издательство ОмГТУ. 644050, г. Омск, пр. Мира, 11; т. 23-02-12.
Типография ОмГТУ.






