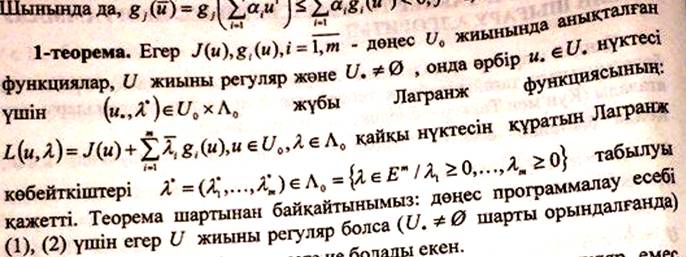
Нүктенің жиындағы проекциясы.Анықтама.Мысалдар
Біртекті әдісімен функцияны минимизациялау.Мысалдар
Мысал:
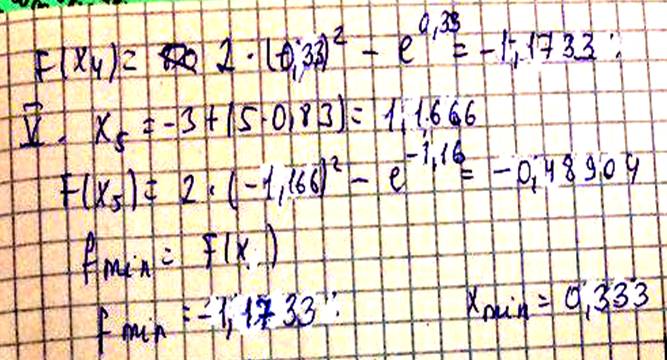
Дихотомия әдісімен функцияны минимизациялау.Мысалдар
Мысал
Алтын қима әдісімен функцияны минимизациялау.Мысалдар
Фибоначи сандары арқылы біртіндеп тиімді іздеу алгоритмі.Мысалдар
Ньютон әдісімен функцияны минимизациялау.Теорема
Ньютон әдісі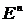 
-дегі 
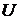жиынындағы 
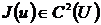минимум іздеу үшін қолданылады. Ньютон әдісін 
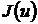-дың 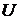-дағы минимумын іздеудің қорытынды кезеңінде, жуықтау 
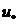нүктесіне жеткілікті жақындаған шақта қолданған жөн.
Айыптық функциялар әдісі - жалпы әдістердің бірі. Оның мағынасы бастапқы есепті белгілі сандық әдістерімен шешілетін қосалқы есеппен алмастыруды білдіреді. Лагранж көбейткіштерінің әдісі Лагранж функциясының қайқы нүктесін іздеуге негізделген.
Ньютон әдісі. Тиімділік есебін қарастырайық:
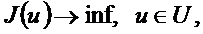
мұндағы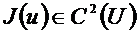 
, 
- 
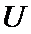- де берілген жиын. (1) - есепті шешу үшін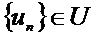 
тізбегі төмендегі алгоритм бойынша құрылады.
1-теорема. Егер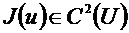 
, 
- дөңес тұйық жиын және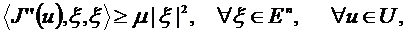 
, онда (2) - шешілетін есеп.
Егер, мұның сыртында, 
- онда келесі баға ақиқат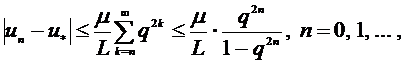 
(4)
мұндағы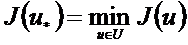 
.
Ньютон әдісінің алгоритімін жазыңыз(бірөлшемді)Мысалдар келтіріңіз
Көп өлшемді ньютон әдісімен функцияны минимизациялау.Мысалдар
Градиенттік әдісті жазыңыз.Теорема
Градиенттік әдіс. Тиімділік есебін қарастырайық:
,
мұндағы 
.
1 теорема. Егер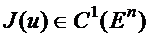 
, 
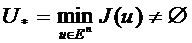және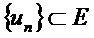 
тізбегі
ережесімен құрылса, градиент J'(и) Липшиц шартын қанағаттандырса:
онда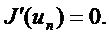 
Егер, мұның сыртында, 
-дөңес,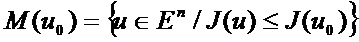 
жиыны шектелген болса, онда 
тізбегі (1) - есеп үшін минимумдаушы болады, яғни
және кез келген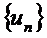 
тізбегінің шеткі нүктесі 
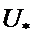жиынында жатады. Төмендегі бағалау ақиқат:
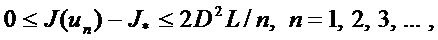
Мұндағы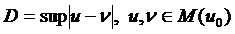 
. 
-де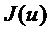 
әлді дөңес болса
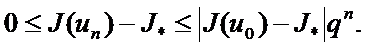
мұндағы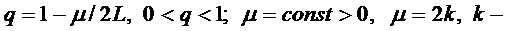 
-дегі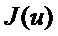 
функциясының әлді дөңестігін білдіретін тұрақты.
дәлелденді.
Градиенттік әдістің алгоритімін келтіріңіз.Мысалдар
Айталық 
. Тиімділік есебін қарастырайық
Функция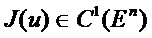 
, ендеше кез келген 
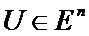векторы үшін
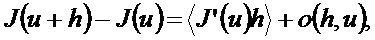
әрі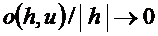 
егер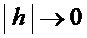 
. Скалярлық көбейтінді қасиетінен (Коши-Буняковский теңсіздігінен):
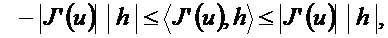
әрі сол жақтағы теңсіздік тек 
кезінде, ал оң жақтағы 
кезінде орындалады. Мәселен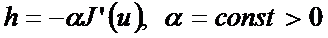 
. Онда (5)-тен шығатыны
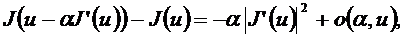
мұндағы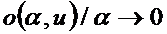 
, егер 
. Сонымен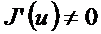 
кезінде 
функциясының 
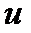нүктесіндегі ең жылдам кему бағыты 
(антиградиент) векторының бағытымен беттеседі екен. Дифференциалданатын функцияларды минимумдаудың градиентті әдістерінің бірқатары осы қасиетке негізделген.
Діс алгоритмі.
1. Бастапқы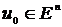 
нүктесі таңдалады. Бастапқы нүктені таңдаудың жалпы ережесі жоқ.
2. 
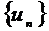тізбегі
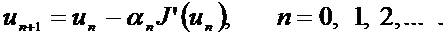
формула бойынша құрылады.
3. 
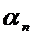саны градиентті әдіс қадамы деп аталып, 
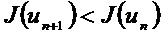шартынан таңдалады:
Градиенттің проекциясы әдісін жазыңыз.Теорема
Есебінін минимумдаушы тизбеги жане онын кез келген шетки нуктеси U
Жиынында жатады.
Градиенттің проекциясы әдісінің алгоритімін келтіріңіз.Мысалдар жазыңыз
