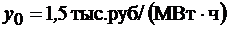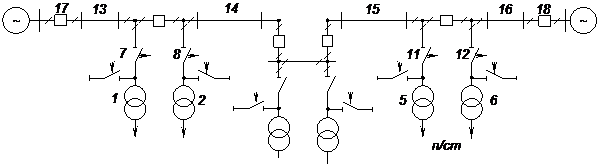Логико-вероятностный метод расчета надежности электроснабжения с помощью дерева отказов

 

Логико-вероятностный метод с использованием дерева отказов является дедуктивным (от общего к частному) и применяется в тех случаях, когда число различных отказов системы относительно невелико. Применение дерева отказов для описания причин отказа системы облегчает переход от общего определения отказа к частным определениям отказов и режимов работы её элементов, понятным специалистам – разработчикам, как самой системы, так и элементов. Переход от дерева отказов к логической функции отказа открывает возможности для анализа причин отказа системы на формальной основе. Логическая функция отказа позволяет получить формулы для аналитического расчёта частоты и вероятности отказов системы по известной частоте и вероятностям отказов элементов. Использование аналитических выражений при расчёте показателей надёжности даёт основание к применению формул теории точности для оценки среднеквадратической погрешности результатов.

Отказ функционирования объекта, как сложное событие, является суммой события отказа работоспособности  и события 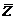, состоящего в появлении критических внешних воздействий. Условие отказа функционирования системы формулируется специалистами в области конкретных систем на основе технического проекта системы и анализа её функционирования при возникновении различных событий при помощи высказываний.

Высказывания могут быть конечными, промежуточными, первичными, простыми, сложными. Простое высказывание относится к событию или состоянию, которые сами не рассматриваются ни как логическая сумма "ИЛИ", ни как логическое произведение "И" других событии или состояний. Сложное высказывание, представляющее собой дизъюнкцию нескольких высказываний (простых или сложных), обозначается оператором "ИЛИ", связывающим высказывания низшего уровня с высказываниями высшего уровня (рис. 4, а).

Рис. 4. Элементы представления логических схем

 

Сложное высказывание, представляющее собой конъюнкцию нескольких высказываний (простых или сложных), обозначается оператором "И", связывающим высказывания низшего уровня с высказываниями высшего уровня (рис. 4, б). Высказывания удобно кодировать так, чтобы по коду можно было судить о том, простое оно или сложное, на каком уровне от конечного расположено и что собой представляет (событие, состояние, отказ срабатывания, тип элемента).

В теории графов деревом называется связный граф, не содержащий замкнутых контуров. Деревом отказов называют логическое дерево (рис. 5), в котором дуги представляют события отказа на уровне системы, подсистем или элементов, а вершины – логические операции, связывающие исходные и результирующие события отказов.

Рис. 5. Пример построения дерева отказов

 

Построение дерева отказов начинается с формулировки конечного высказывания об отказе системы. Для характеристики безотказности системы конечное высказывание относят к событию, которое приводит к нарушению функционирования в рассматриваемом интервале времени, при заданных условиях. То же для характеристики готовности.

В

Пример. Построим дерево отказов для схемы сети, приведенной на рис. 6.

Рис. 6. Схема сети

 

Подстанции В и С питаются от подстанции А. Конечным событием дерева отказов является отказ системы в целом. Этот отказ определяется как событие, заключающееся в том, что

1) либо подстанция В, либо подстанция, С полностью теряют питание;

2) мощность для питания суммарной нагрузки подстанций В и С приходится передавать по одной единственной линии.

Исходя из определения конечного события и принципиальной схемы системы, строим дерево отказов (вниз от конечного события) (рис. 7).

Цель анализа дерева отказов состоит в том, чтобы определить вероятность конечного события. Поскольку конечное событие есть отказ системы, анализ дает вероятность Р(F).

Метод анализа основан на нахождении и расчете множеств минимальных сечений. Сечением называют такое множество элементов, суммарный отказ которых приводит к отказу системы. Минимальное сечение – такое множество элементов, из которого нельзя удалить ни одного элемента, иначе оно перестаёт быть сечением.

Рис. 7. Дерево отказов системы по схеме рис. 6

– отказы подсистем, которые можно анализировать далее;

– отказы элементов, которые далее не анализируются.

Передвигаясь на один уровень ниже от вершинного (конечного) события, проходим через узел "ИЛИ", который указывает на существование трёх сечений: { P }, { Q }, { R }, (Р, Q, R – события отказов). Каждое из этих сечений может быть разделено далее на большее число сечений, но может выясниться, что отказ сечений обуславливается несколькими событиями, в зависимости от того, какой тип логического узла встречается на пути следования.

Например, {Q} сначала превращается в сечение {3, Т }, затем Т разделяется на сечения { Х,У }, в результате вместо одного сечения {3, Т } появляются два: {3, X }, {3, У }.

На каждом из последующих шагов выявляются множества сечений:

Минимальными сечениями являются выделенные сечения {3,4,5}, {2,3}, {1,3}, {1,2}. Сечение {1,2,3}, не минимальное, поскольку {1,2} – тоже сечение. На последнем шаге множества сечений состоят исключительно из элементов.

 

4.4. Расчёт надежности двухцепной линии

Для составления схемы надежности в исходной схеме электрической сети объединяются все источники питания, а линии замещаются блоками, связанными между собой и с потребителем и источниками питания так, как в исследуемой схеме сети. На рис. 8. показана схема сети и операция составления схемы надежности.

 

Рис. 8. а) – Исходная схема сети; б) схема надежности

Для большей наглядности схему надежности можно привести к виду, где шины источников питания ИПи шины потребителя (П) представлены параллельными прямыми

 

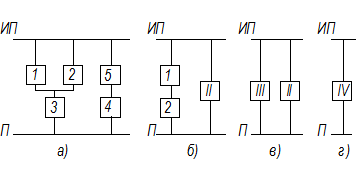
Рис. 9. Упрощенная схема надежности

 

Двухцепные линии в схеме надежности представляются тремя блоками, как показано на рис. 10. Блоки 1 и 2отражают отказы и плановые ремонты каждой из цепей отдельно, а блок 1-2 – одновременные отказы обеих цепей.

Для схем сети без замкнутых контуров схема надежности содержит лишь последовательно и параллельно соединенные блоки (рис. 8 а и б). При наличии в сети замкнутых контуров в схеме надежности появляются пёремычки между параллельными ветвями (рис. 11).

Расчет по схеме надежности проводится путем ряда преобразований последовательно или параллельно включенных блоков в эквивалентные до тех пор, пока шины источника питания и потребителя не окажутся связанными одним эквивалентным блоком (рис. 9 б и в ). Показатели надежности этого блока (рис. 9,г) и являются искомыми показателями надежности электроснабжения потребителя.

 

 

 

Рис. 10. К расчёту показателей надежности двухцепной линии

Рис. 11.

Для п последовательно включенных блоков показатели надежности эквивалентного блока приближенно (без учета возможности их одновременных простоев) определяются по формулам (1-6)

Для двух параллельно включенных элементов i и j эквивалентный блок характеризуется только показателями надежности, так как одновременные плановые простои элементов предполагаются недопустимыми. Показатели надежности эквивалентного блока

          (2-22)

        (2-23)

 

где Т_В;В - средняя длительность одновременного вынуж­денного простоя, равная согласно выражениям (2-6) —(2.8):

 

                                            (2-24)

 

Т_{В i ;П j} и Т_{В j ;П i} - средние длительности одновременного, простоя при наложении отказа на плановый ремонт, определяемые по (2-13) или (2-14).

Если пропускная способность отдельных связей меж­ду потребителем и источниками питания или мощность

 

                

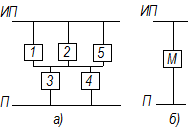
Рисунок 12

 

отдельных источников не может обеспечить полного снабжения потребителя электроэнергией, то кроме пере­рывов электроснабжения, определяемых показателями надежности результирующего блока (например, блок IV рис. 2-б,г), необходимо учитывать режимы, в которых происходит ограничение электроснабжения. Так, если в схеме на рис. 2-5,а пропускная способность линий Л4 и JI 5 или мощность источника питания ИПЗ меньше на­грузки потребителя, то возможны ограничения потреби­теля, математические ожидания и длительности которых определяются показателями надежности и плановых простоев блока III (рис. 2-6, в).

Для блок-схем с перемычками (рис. 2-8) рассчиты­ваются характеристики эквивалентных блоков для двух схем, получаемых из исходной, а именно: первой (рис. 2-9,а), в которой в перемычке нет блока, т. е. без учета вынужденных и плановых простоев блока; второй (рис. 2-10, а), в которой пермычка вообще отсутствует. По полученным показателям надежности этих схем шм; Т_ВМ (рис. 2-9,6) ω_L; T _bL(рис. 2-10,6) и известным коэффициентам вынужденного и планового простоев блока перемычки К_{В i} и K _{П i} вычисляются результирую­щие показатели надежности электроснабжения:

 

               (2-25)

       (2-26)

 

В качестве примера произведем расчет математического ожида­ния перерывов электроснабжения и их средней длительности для схемы, приведенной на рис. 2-5,а.

Параметры линий электропередачи и их показатели надежности даны в табл. 2-1. Возможность проведения плановых ремонтов линий в периоды с благоприятными климатическими условиями учтена коэффициентом k_ω = 0,5.

 

Линия	Напряже­ние, кВ	Длина, км	ω, 1/год	T В, ч	μ, 1/год	T п, ч
1	220	100	0.7	16	6	8
2	220	120	0.84	16	6	8
3	110	50	0.5	14	5	8
4	110	60	0.6	14	5	8
5	110	40	0.4	14	5	8

Таблица 2-1

 

1. Расчет показателей надежности блока /, эквивалентного па­раллельно включенным блокам 1 и 2 (рис. 2-6,а, б).

Коэффициенты вынужденного и планового простоев блоков 1 и 2в соответствии с (1-6)' и (1-9):

 

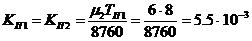
Параметр потока отказов блока I в соответствии с (2-22)

Длительность одновременного вынужденного простоя при наложении отказа на плановый ремонт в соответствии с формулой (2-13)

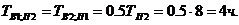
Среднее время восстановления блока I в соответствии с (2-23)

 

2. Расчёт показателей надёжности плановых простоев блока II, эквивалентного последовательно соединённым блокам 4 и 5.

Параметр потока отказов и среднее время восстановления блока II, в соответствии с (2-18) и (2-19)

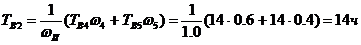
Частота и средняя продолжительность плановых простоев блока II в соответствии с (2-20) и (2-21)

Показатели надёжности блоков III и IV рассчитываются аналогично. Результаты расчёта сведены в таблицу 2-2

Блок	ω, 1/год	T В, ч	μ, 1/год	T п, ч
I	0.006	5.3	0	0
II	1.0	14	10	8
III	0.506	14	5	8
IV	0.006	4.6	0	0

 Таблица 2-2

 

Из таблицы 2-2 можно видеть, что полные перерывы электроснабжения характеризуются математическим ожиданием числа перерывов, равным 0.006 1/год, или равно примерно 1 раз за 170 лет при средней длительности вынужденных простоев 4.6 ч. Плановые перерывы электроснабжения отсутствуют.

При недостаточных пропускной способности линий Л4 и Л5 или мощности источника питания ИП3 ограничения потребителя будут при вынужденных и плановых простоях блока III: математическое ожидание вынужденных ограничений равно 0.506 или 1 раз за 2 года при средней длительности 14 часов; плановые ограничения 5 раз в год при длительности 8 часов.

СПИСОК ЛИТЕРАТУРЫ

1. Ю.Е. Гуревич, К.В. Кабиков. Особенности электроснабжения, ориентированного на бесперебойную работу промышленного потребителя. М.: Изд-во «ЭЛЕКС-КМ», 2005.
2. ГОСТ 27.002-89. Межгосударственный стандарт. Надежность в технике. Основные понятия термины и определения. М. Изд-во стандартов, 2002.
3. ГОСТ 21027-75. Системы энергетические. Термины и определения. М.: Изд-во стандартов, 1987.
4. Папков Б.В. Терминология современной электроэнергетики / Б.В. Папков: Нижегород. гос. тех. ун-т. – Н. Новгород: Изд-во Волго-Вятской академии гос. Службы, 2006. – 92 с.
5. ГОСТ 19431-84. Энергетика и электрификация термины и определения. М.: Изд-во стандартов, 1984.
6. ГОСТ 27.004-85. Межгосударственный стандарт. Надежность в технике. Системы технологические. Основные понятия термины и определения. М. Изд-во стандартов, 2002.
7. ГОСТ 13109-97. Межгосударственный стандарт. Качество электрической энергии. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. М. Изд-во стандартов, 2002.
8. Правила технической эксплуатации электроустановок потребителей. М.: Изд-во НЦ ЭНАС, 2003.
9. Правила технической эксплуатации электрических станций и сетей Российской Федерации. М.: Изд-во НЦ ЭНАС, 2003.
10. Л.К. Осика. Организационные и технические мероприятия по обеспечению надежности электроснабжения потребителей – субъектов оптового и розничного рынков электроэнергии // Электрика № 6, 2004. С. 3-11.
11. Правила устройства электроустановок. Раздел 1. Общие правила. Глава 1.2. 7-е изд. М.:.: Изд-во НЦ ЭНАС, 2002, 184 с.
12. Гук Ю.Б. Теория надежности в электроэнергетике. М.: Энергоатомиздат­ – 1990., 206с., ил.
13. Папков Б.В., Пашали Д.Ю. Надежность систем электроснабжения / Учеб. пособие / Б.В. Папков, Д.Ю. Пашали УГАТУ, Уфа.: изд-во УГАТУ – 2007, 192 с., ил.
14. Розанов М.Н. Надежность электроэнергетических систем. М.: Наука – 1974., 175 с., ил.
15. Надежность систем энергетики и их оборудования. Справочник в 4-х т./ Под общ. ред. Ю.Н. Руденко. Т.2. Надежность электроэнергетических систем / Справочник. М.: Энергоатомиздат­ – 2000., 568с., ил.
16. Шалин А.И. Надежность и диагностика релейной защиты энергостистем / Учебное пособие. Н.-Новгород: изд-во НГТУ, 384 с. ил.
17. Трубицын В.И. Надежность электростанций: Учебник для вузов. – М.: Энергоатомиздат, 1997., 240 с.: ил.
18. Солдаткина Л.А. Электрические сети и системы: Учебное пособие для вузов. – М.: Энергия, 1978., 216 с., ил.

 

ПРИЛОЖЕНИЕ А

Данные для расчёта надежности электроснабжения потребителей

Таблица А.1

 

Элемент	№ на схеме	, 1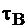/год	, год
Трансформатор	1-6	0,02	0,02	0.007
Короткозамыкатель с отделителем	7-12	0,04	0,0004	0.001
Участок одноцепной воздушной линии	13-16	0,5	0,001	0.005
Выключатель масляный	17-20	0,03	0,003	0.006
Данные для расчёта двухцепных линий интенсивность ремонтов , Длительность планового ремонта
Данные для расчёта ущерба ,

 

 

ПРИЛОЖЕНИЕ Б

 

ВАРИАНТЫ ЗАДАНИЙ НА КУРСОВОЕ ПРОЕКТИРОВАНИЕ

СХЕМА 1