При измерении любой физической величины невозможно определить истинное значение этой величины.
Это связано:
- с несовершенством измерительной аппаратуры
- с несовершенством органов чувств экспериментатора
- с изменчивостью внешних условий (температура, вибрация, движение потоков воздуха)
Разность между измеренным и истинным значениями физической величины называется погрешностью (ошибкой) измерения.
В зависимости от причины возникновения погрешностей их можно разделить на следующие виды:
1) Методические погрешности
Вызываются недостатками применяемого метода измерения, несовершенством теории физического явления, неточностью расчетной формулы. Например, при взвешивании тела на весах не учитываются не одинаковые выталкивающие силы, действующие на тела и на гири.
Методические погрешности могут быть уменьшены при изменении и усовершенствовании метода измерения, при введении уточнений или поправок в расчетные формулы.
2) Приборные погрешности
Вызываются несовершенством конструкции и неточностью изготовления измерительных приборов. Уменьшение приборной погрешности достигается применением более точных (и более дорогих) приборов.
3) Случайные погрешности
Вызываются факторами, не поддающимися учету, например, изменением внешних условий. Уменьшение случайной погрешности достигается за счет многократного повторения измерений. При этом влияние факторов, приводящих к завышению или занижению результатов измерений, может частично скомпенсироваться.
При расчетах рассматриваются:
1) Абсолютная погрешность – это модуль разности между истинным и измеренным значением
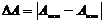 .
.
Зная абсолютную погрешность можно определить интервал, в котором лежит истинное значение измеряемой величины
 .
.
Интервал от 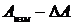 до
до 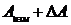 называется доверительным интервалом.
называется доверительным интервалом.
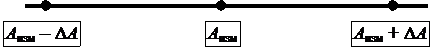 |
Вероятность, с которой истинное значение попадает в доверительный интервал, называется доверительной вероятностью, или надежностью данных.
2) Относительная погрешность εА:
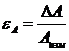 .
.
Относительная погрешность определяет точность проведенных измерений и выражается в процентах.
Приборная погрешность.
На шкалах многих электроизмерительных приборов указывается класс точности (0,5; 1; 1,5; 2). Класс точности определяет абсолютную приборную погрешность в процентах от наибольшего значения, которое может быть измерено прибором.
Например, миллиамперметр со шкалой 300 мА и классом точности 1,5 дает абсолютную приборную погрешность ΔI = 1,5%·300 мА = 4,5 мА в любом месте шкалы.
Абсолютная приборная погрешность:
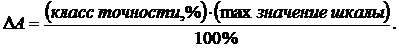
Если класс точности на приборе не указан, то абсолютную погрешность берут равной половине цены наименьшего деления.
Например, для миллиметровой линейки Δ А = ± 0,5 мм, для микрометра (цена деления 0,01мм) Δ А = ± 0,005 мм.
При определении общей (результирующей) абсолютной погрешности учитывают и случайную, и приборную погрешности:
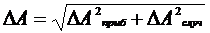 .
.
Физические измерения бывают 2-х видов:
Прямые – измерение физической величины производится непосредственно прибором.
Косвенные – физическая величина рассчитывается по формуле.
Обработка результатов прямых измерений
1) Производят измерения физической величины n раз (серию измерений):
А 1, А 2,… А n (n = 3-5) затем находят среднее значение измеряемой величины
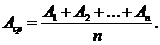
2) Находят абсолютную случайную погрешность каждого измерения:
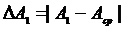 ,
, 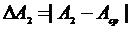 ,
, 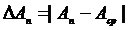 .
.
Окончательное значение случайной погрешности принимают равным максимальному ее значению в серии измерений.
Принимая во внимание то, каким прибором проводилось измерение, находят приборную погрешность Δ А приб.
Окончательное (результирующее) значение абсолютной погрешности:
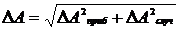 .
.
Если Δ А случ >> Δ А приб, то Δ А = Δ А случ, и в дальнейших расчетах учитывается только случайная погрешность.
Если Δ А случ << Δ А приб, то Δ А = Δ А приб, и в дальнейших расчетах учитывается только приборная погрешность.
Окончательный результат записывается в виде:
А = (А изм ± Δ А) (размерность измеряемой величины).
Обработка результатов косвенных измерений
Пусть физическая величина А связана с несколькими величинами x 1, x 2… xn некоторой функциональной зависимостью A = f (x 1, x 2… xn), например, R = U / I, R = ρ ℓ / S и т.д.
Среди величин x 1, x 2… xn могут содержаться прямо измеряемые величины, а также заранее известные табличные величины, данные установки. Пусть в результате обработки всех величин, найдены их средние значения x 1ср, x 2ср… xn ср и абсолютные погрешности Δ x 1, Δ x 2… Δ xn. Тогда результат для косвенно измеряемой величины получают по следующей схеме:
1) среднее значение рассчитывают по формуле:
A = f (x 1ср, x 2ср… xn ср);
2) по виду функциональной зависимости находят относительную погрешность с помощью логарифмического дифференциала:
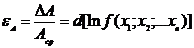
После нахождения значения εА находят абсолютную погрешность Δ А:
Δ А = А ср·εА.
Окончательный результат записывают в виде:
А = (А ср ± Δ А) (размерность).
Примеры нахождения ε для наиболее простых функций:
| Функция | Относительная погрешность |
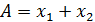
| 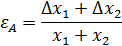
|
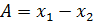
| 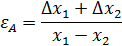
|
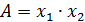
| 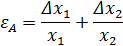
|
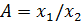
| 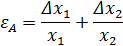
|
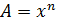
| 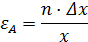
|
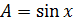
| 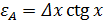
|
Следует обратить внимание на то, что погрешности всегда складываются.
В расчетных формулах часто встречаются величины, взятые из таблицы (π, е т.п.).
В значении универсальной постоянной, например, числа π, надо взять столько значащих цифр, чтобы относительная погрешность этой постоянной (επ) была на порядок (в 10 раз) меньше, чем суммарная относительная погрешность измеренных величин, тогда επ не будет заметно увеличивать результирующую погрешность.
Например, π ≈ 3,14159. Пусть ε = 1%, тогда если взять π = 3,1, то погрешность округления Δπ = 3,1415–3,1 = 0,04 и
επ = Δπ/π = 0,04/3,1 = 0,013 = 1,3%.
В этом случае επ ~ ε и к результирующей погрешности добавляется 1,3% «из ничего»!
Если же взять π = 3,14, то Δπ = 3,1415–3.14 = 0,002. Тогда относительная погрешность округления числа π составляет επ = Δπ/π = 0,002/3,14 = 0,1%, т.е. на порядок меньше погрешности измерения, и почти не влияет на общую погрешность.
Такие же рассуждения следует применять для величин, значения которых берутся в справочных таблицах, а также для иррациональных чисел, входящих в формулы.
Если в значении величин, заданных на установках не указаны абсолютные погрешности, то считается, что они измерены с точностью равной половине единицы последнего указанного разряда:
m = 8 г → Δ m = 0,5 г;
m = 8,3 г →Δ m = 0,05 г.
Окончательная запись результатов измерений:
1) Округление результатов рекомендуется начать с округления абсолютной погрешности: в погрешности оставляют одну значащую цифру; если же старшая значащая цифра погрешности 1 или 2, то рекомендуется округлять погрешность до двух цифр.
2) Окончательный результат измерений Аср округляют или уточняют «до погрешности»: последняя (младшая) значащая цифра в результате находится в том же разряде, что и в погрешности.
3) Окончательно имеем: А = (А изм ± Δ А) ед.




