Кинематика вращательного движения

 

При криволинейном движении ускорение имеет две составляющих – нормальную (a_n) и тангенциальную (a _t).

Нормальная составляющая ускорения характеризует быстроту изменения направления скорости (направлена по главной нормали к центру кривизны траектории), тангенциальная составляющая ускорения характеризует быстроту изменения модуля скорости (направлена по касательной к траектории). Модули этих ускорений равны

Составляющие a_n и a _t перпендикулярны друг к другу. Модуль полного ускорения равен

Кинематическое уравнениеравнопеременного вращательного движения

,

где j – угол поворота; j₀ – начальный угол поворота; w – скорость угловая; e – ускорение угловое.

Модуль мгновенной угловой скорости

,   

Модуль мгновенного углового ускорения

.

Связь между линейными и угловыми величинами, характери­зующими движение точки по окружности, выражается уравнениями

s = j R,    υ = w R,   a _t   = e R,   a_n = w² R,

где υ – линейная скорость; a _t и a_n – тангенциальная и нормальная составляющие ускорения; w – угловая скорость; e – угловое ускорение; R – радиус окружности.

 

Импульс материальной точки. Законы Ньютона.

Силы в природе

Количество движения (импульс) материальной точки массой m, движущейся поступательно со скоростью υ, равен

.

Уравнение движения материальной точки в векторной форме (второй закон Ньютона) имеет вид

, ,

при m = const

где – геометрическая сумма сил, действующая на материальную точку (равнодействующая сил).

Сила упругости F _упр = – kx, где k – коэффициент упругости (жесткость в случае пружины); х – абсолютная деформация тела.

Сила тяжести F _тяж = mg.

Сила тренияскольжения F = µ N, где µ – коэффициент трения скольжения; N – сила нормального давления, с которой одно тело действует на другое;

Сила гравитационного взаимодействия (закон всемирного тяготения)

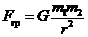
где G – гравитационная постоянная; m ₁ и m ₂ – массы взаимодействующих тел; r – расстояние между телами (тела рассматриваются как материальные точки).

Закон сохранения импульса. Центр масс

 

Закон сохранения импульса выражается формулой

,

где  – импульс системы; – импульс i -й материальной точки; N – число материальных точек в системе.                      

Центр масс (или центр инерции) системы материальных точек – это воображаемая точка С, положение которой характеризует распределение массы этой системы. Ее радиус вектор равен

где m_i и  – масса и радиус-вектор i -й материальной точки соответственно; N – число материальных точек в системе; – масса системы.            

Скорость центра масс

Импульс системы можно рассчитать по формуле .