Энергия затухающих колебаний складывается из потенциальной и кинетической: Ε = kx 2/2 + т  /2. После подстановки в предыдущую формулу выражений x (t)и
/2. После подстановки в предыдущую формулу выражений x (t)и  (t), соответствующих затухающим колебаниям (8), получим зависимость E (t), которая графически представлена на рис. 4. Уменьшение энергии колебаний обусловлено работой силы сопротивления. Мощность этой силы определяется как
(t), соответствующих затухающим колебаниям (8), получим зависимость E (t), которая графически представлена на рис. 4. Уменьшение энергии колебаний обусловлено работой силы сопротивления. Мощность этой силы определяется как
– r  ·
·  = – r
= – r  ,
,
тогда
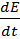 = – r
= – r  .
.
Таким образом, 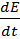 <0, кроме тех случаев, когда
<0, кроме тех случаев, когда  =0. При малом затухании (β<<ω0) зависимость E(t)становится практически экспоненциальной:
=0. При малом затухании (β<<ω0) зависимость E(t)становится практически экспоненциальной:
 , (11)
, (11)

Рисунок 4
отсюда можно определить убыль энергии в единицу времени:
– 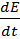 =2β E (12)
=2β E (12)
Характеристики затухания
Кроме коэффициента β затухание характеризуют и другими величинами:
1. Время релаксации τ — физическая величина численно выражающая промежуток времени, за который амплитуда затухающих колебаний уменьшается в е раз. Из выражения а = а 0е-β t видно, что
 =
=  (13)
(13)
Интервал времени τназывают также постояннойвремениосциллятора. Это оценка времени, в течение которого продолжается процесс свободных колебаний осциллятора, выведенного из положения равновесия. Разумеется, по истечении времени τколебания продолжаются, но амплитуда, спадая по экспоненциальному закону, становится столь малой, что практически можно полагать, что колебания прекратились (скажем, через промежуток времени 5/βамплитуда падает более чем в 100 раз).
2. Логарифмический декремент затухания.
Логарифмический декремент затухания (λ) -безразмерная физическая величина показывающая уменьшение амплитуды колебательного процесса за один периоди численно равная натуральному логарифму отношения двух последовательных амплитуд, взятых через период
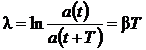 , (14)
, (14)
где: Т — период затухающих колебаний.
Например, при λ = 0,01 амплитуда колебаний изменяется за 1 период приблизительно на 1%. Из формул (13) и (14) следует, что
λ=  =
=  ,(15)
,(15)
где N e — число колебаний за время τ, в течение которого амплитуда уменьшается в е раз.
3. Добротность осциллятора. При малых значениях логарифмического декремента:
Q =  =π N e(16)
=π N e(16)
Эту величину применяют для характеристики чувствительности колебательной системы к резонансным воздействиям. Из (16) следует, что добротность пропорциональна числу колебаний N e, совершаемых системой за время релаксации.
В заключение отметим, что анализ формулы (10) приводит к выводу: затухающие колебания возможны при условии β < ω 0. Хотелось бы обратить внимание, что при увеличении коэффициента затухания β период затухающих колебаний будет расти, и при β = ω 0 система будет совершать апериодическое движение: выведенная из положения равновесия, она возвращается в это положение, не совершая колебаний.
Порядок выполнения работы
Задание 1. Определение коэффициента жесткости пружины статическим методом
1. С помощью крепежного винта подвесьте пружину вертикально к горизонтальному стержню. К пружине уже прикреплен небольшой груз. Получившаяся конструкция представляет собой пружинный маятник.
2. На стенде, расположенном напротив пружины, установите линейку, которая будет необходима для определения удлинений пружины в ходе работы. Зафиксируйте координату нижней плоскости груза в положении равновесия (от этой точки далее будет производиться отсчет координаты x).
3. Проведите последовательно прямые измерения координаты x относительно начального положения для грузиков различных масс (пять опытов с грузиками, отличающимися по массе!).
4. Считая условием равновесия mg = kx, постройте график зависимости mg (x) (значение ускорения свободного падения g принимайте равным 9.81 м/с2 без погрешности). Если деформации пружины упругие, т. е. после прекращения действия силы пружина восстанавливает первоначальные геометрические параметры (на практике это условие выполняется при малых удлинениях пружины), то закон Гука справедлив (k = const) и график будет линейным. Тангенс угла наклона полученной прямой дает среднее значение коэффициента жесткости k. Таким образом, для произвольной точки прямой  .
.
5. Погрешностью отдельного прямого измерения величин, отложенных на осях, считают отклонение экспериментального значения рассматриваемой величины от значения, даваемого графиком. Установив таким образом относительные погрешности всех отдельных прямых измерений для m и x, усредните их по пяти измерениям.Таким образом, погрешность k будет определяться выражениями  ,
,  .
.
6. Заполните таблицу, используя полученные данные:
| № измерения | m, г | ε m | 
| x, мм | ε x | 
| 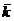 , н/м , н/м
| ε k, % | Δ k, н/м |
| 1 |
|
|
|
|
| ||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 |
7. Представьте конечный результат в виде:  ,
,  .
.
Задание 2. Определение коэффициента жесткости пружины динамическим методом
1. Для пяти различных масс найдите время t двадцати полных колебаний. Груз от положения равновесия необходимо отклонять строго вертикально. Отклонение от положения равновесия не должно быть более 20 мм.
2. Вычислите период T по формуле: T = t / n, где n = 20 – число колебаний (в этом задании затуханием колебаний необходимо пренебречь).
3. Т. к. 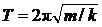 , то
, то  . Ввиду того, что
. Ввиду того, что  , зависимость T 2(m) получается линейной, и ее график должен представлять собой прямую. Постройте его. Поуглунаклонапрямойопределите
, зависимость T 2(m) получается линейной, и ее график должен представлять собой прямую. Постройте его. Поуглунаклонапрямойопределите 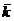 = 4π2 ctgα.
= 4π2 ctgα.
4. С помощью графика установите относительные погрешности всех отдельных прямых измерений m и T 2 , а такжеусредните их по пяти измерениям (см. п.5 предыдущего задания).Таким образом, погрешность k будет определяться выражениями  ,
, 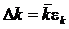 .
.
5. Заполните таблицу, используя полученные данные:
| № измерения | m, г | ε m | 
| t, с | n | T, с | T 2, с2 | 
| 
| 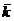 , н/м , н/м
| ε k, % | Δ k, н/м |
| 1 |
| 20 |
|
|
|
| ||||||
| 2 | ||||||||||||
| 3 | ||||||||||||
| 4 | ||||||||||||
| 5 |
6. Представьте конечный результат в виде:  ,
, 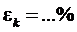 .
.
Задание 3. Определение характеристик затухания
1. Отклоните строго вертикально груз определенной массы m от положения равновесия, растягивая пружину на а 0 = 27 мм. Зафиксируйте положение амплитуды, меньшей в е раз: а ≈ 10 мм.
2. Отпустите пружину, включив секундомер, и считайте колебания до тех пор, пока нижняя плоскость груза не перестанет пересекать отметку, сигнализирующую об уменьшении амплитуды в е раз. По достижении упомянутого момента выключите секундомер, зафиксировав время t и число N еколебаний.
3. Повторите опыт еще 2 раза и занесите экспериментальные данные в таблицу:
| № опыта | а 0, мм | а, мм | t, с | N е | T, с |
| 1 | |||||
| 2 | |||||
| 3 |
4. Оцените абсолютные и относительные погрешности а 0, а, t, T.
5. Рассчитайте значения и оцените погрешности следующих величин:
логарифмического декремента затухани я λ, воспользовавшись формулой (15);
времени релаксации 𝜏, преобразовав формулу (15);
коэффициента затухания β, преобразовав формулу(13);
добротности осциллятора Q, воспользовавшись формулой (16).
6.Данные, полученные в п. 4, п. 5 представьте в виде таблицы. Вид таблицы выберите самостоятельно.
7. Представьте окончательные результаты в виде:
 ,
,  ;
;
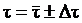 ,
,  ;
;
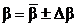 ,
,  ;
;
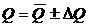 ,
,  .
.
8. Сделайте выводпо проделанной работе.
Контрольные вопросы
1. Что такое деформация? Какие виды деформаций вы знаете? Чем они отличаются друг от друга? Прикакихусловияхнапрактикедеформацииможнопринятьупругими?
2. Сформулируйте закон Гука. Укажите границы применимости этого закона.
3. Какие колебания называются незатухающими? Выведите дифференциальное уравнение, описывающее незатухающие колебания.
4. Какие колебания называются затухающими? Выведите дифференциальное уравнение, описывающее затухающие колебания.
5. Можно ли назвать затухающие колебания строго периодическими? Почему?
6. Как зависит от времени энергия затухающих колебаний?
7. Что такое коэффициент затухания, время релаксации, логарифмический декремент затухания, добротность осциллятора?
8. В чем заключается сущность статического метода определения коэффициента жесткости?
9. В чем состоит сущность динамического метода определения коэффициента жесткости?
Литература
а) основнаялитература:
5. Детлаф А.А., Яворский Б.М. Курс физики: учебн. пособие для студентов втузов. - 8-е изд., стер.-М.: Академия, 2009. - 720 с.
6. Савельев И.В. Курс физики: учеб.пособие для вузов. Т. 1: Механика. Молекулярная физика. — 4-е изд., стер. — СПб.: Лань, 2008. — 352 с.
7. Трофимова Т.И. Физика: учебник для высшего проф. образования. - М.: Академия, 2012. - 320 с.
8. Трофимова Т.И. Курс физики: учеб. пособие для инженерно - техн. спец. вузов. - 18-е изд,, стер. - М.: Академия, 2010. – 560 с.
б) дополнительнаялитература:
1. Иродов И.Е. Механика. Основные законы. – 8-е изд., стер. – М.: БИНОМ. Лабораториязнаний, 2006. – 309 с.
в) ресурсы информационно-телекоммуникационной сети «Интернет»:
1. Электронная библиотека Попечительского совета механико-математическогофакультета Московского государственного университета.- [Электронный ресурс]. Систем.требования: AdobeAcrobatReader. – URL: http://lib.mexmat.ru/books/6791
2. Электронная библиотека РГБ. -[Электронный ресурс]. Систем.требования: AdobeAcrobatReader. – URL: http://elibrary.rsl.ru
3. Электронная научная библиотека Астраханскогогосударственного технического университета - [Электронный ресурс]. Систем.требования: AdobeAcrobatReader. – URL: http://library.astu.org
г) методические указания для обучающихся по освоению дисциплины (модуля):
1. Быкова В.П., Ревина А.В. Методическое пособие для подготовки студентов к Интернет-экзамену по физике. Часть I. Механика. - Астрахань: Изд-во АГТУ, 2009. - 20 с.
2. Быкова В.П., Березина И.С., Ревина А.В. Сборник вопросов и задач для контроля качества знаний студент (для бакалавров). - Астрахань: Изд-во АГТУ, 2011. – 35 с.
3. Селиванов Н.В., Неупокоева И.В. Физический практикум «Механика» (Часть II):
учебно-методическое пособие для студентов инженерно-технических специальностей. - Астрахань: Изд-во АГТУ, 2007. - 36 с.
Лабораторная работа №4






