Теорема сложения если 2 события не совместимы

Следствие 2. Если события А и В несовместны, то т_АВ = 0, и, следовательно, вероятность суммы несовместных событий равна сумме их вероятностей: Р (А + В) = р (А) + р (В).    

Противоположными событиями называют два несовместных события, образующих полную группу. Если одно из них назвать А, то второе принято обозначать .

Замечание. Таким образом,  заключается в том, что событие А не произошло.

 

 

 

Теорема умножения вероятностей. Теорема умножения для независимых событий. Вероятность появления хотя бы одного события.

Назовем условной вероятностью р (В/А) события В вероятность события В при условии, что событие А произошло.

Замечание. Понятие условной вероятности используется в основном в случаях, когда осуществление события А изменяет вероятность события В.

(теорема умножения). Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло:

р (АВ) = р (А) · р (В/А). (2.6)

Доказательство.

Воспользуемся обозначениями теоремы 2.1. Тогда для вычисления р (В/А) множеством возможных исходов нужно считать т_А (так как А произошло), а множеством благоприятных исходов – те, при которых произошли и А, и В (т_АВ). Следовательно,

 

 откуда следует утверждение теоремы.

Следствие.  Если подобным образом вычислить вероятность события ВА, совпадающего с событием АВ, то получим, что р (ВА) = р (В) · р (А/В). Следовательно,

р (А) · р (В/А) = р (В) · р (А/В).              (2.7)

Событие В называется независимым от события А, если появление события А не изменяет вероятности В, то есть р (В/А) = р (В).

Замечание. Если событие В не зависит от А, то и А не зависит от В. Действительно, из (2.7) следует при этом, что р (А) · р (В) = р (В) · р (А/В), откуда р (А/В) = р (А). Значит, свойство независимости событий взаимно.

Теорема умножения для независимых событий имеет вид:

р (АВ) = р (А) · р (В),                                                                       

то есть вероятность произведения независимых событий равна произведению их вероят-ностей.

При решении задач теоремы сложения и умножения обычно применяются вместе.

  Вероятность появления хотя бы одного события.

Теорема. Вероятность появления хотя бы одного из попарно независимых событий

А ₁, А ₂,…, А_п равна        р (А) = 1 – q ₁ q ₂… q_n,    (2.9)

где q_i – вероятность события , противоположного событию А _i.

Доказательство.

Если событие А заключается в появлении хотя бы одного события из А ₁, А ₂,…, А_п, то события А и  противоположны, поэтому по теореме 2.2 сумма их вероятностей равна 1. Кроме того, поскольку А ₁, А ₂,…, А_п  независимы, то независимы и , следовательно, р () = 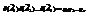. Отсюда следует справедливость формулы (2.9).