Тема 2: Методы решения СЛАУ

Тема 1: Основные понятия курса

П.1 Характеристики алгоритмов:

¾ Погрешность

¾ Трудоемкость

¾ Требование памяти

П.2 Абсолютная и относительная погрешности:

x - приближенное значение некоторой величины

- точное

- абсолютная погрешность
- относительная погрешность (должна быть <<1)

П.3 Изменение абсолютной и относительной погрешностей при арифметических операциях:

Теорема 1.1:

При сложении и вычитании приближенных величин абсолютные погрешности складываются (абсолютная погрешность суммы (разницы) не превосходит суммы абсолютных погрешностей).

Доказательство:

приближенное точное значение абсолютная погрешность суммы

значение суммы суммы

Теорема 1.2:

При перемножении (делении) приближенных величин относительные погрешности складываются (т.е. относительная погрешность произведения (частного) не превышает суммы относительных погрешностей).

Доказательство:

П.4 Изменение погрешности при вычислении функции:

Теорема 1.3:

При вычислении функции абсолютная погрешность умножается на

Следствие 1.4:

При вычислении степенной функции () относительная погрешность умножается в раз.

Доказательство:

Следствие 1.5:

При вычислении экспоненты

относительная погрешность результата равна абсолютной погрешности аргумента.

Замечание 1.6:

Если многократно суммировать приближенные величины одного порядка, то абсолютная погрешность будет увеличиваться не в n раз, а в раз (так как количество “+” и “-” примерно равно(n слагаемых)).

П.5 Источники погрешности:

v Исходные данные

v Округление чисел при машинном вычислении

v Погрешность вычислительных методов

Тема 2: Методы решения СЛАУ

П.1 Точные и приближенные методы решения СЛАУ:

В дальнейшем будем считать n=k

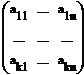Ax=b

A= , b=

Методы решения СЛАУ делятся на 2 группы точные и приближенные:

o Точные (т.е. методы, которые дают точное решение за конечное число шагов при условии, что все действия выполняются абсолютно точно).

o Приближенные (итерационные)

При применении этих методов точного решение никогда не будет получено, оно является пределом последовательности приближенных решений.

Точные методы: метод Гаусса, метод Крамера, через обратную матрицу,...

Приближенные методы: метод простой итерации, метод Зейделя,...

1. Метод Гаусса:

Основная идея: привести исходную матрицу А к треугольному виду с помощью элементарных преобразований строк, после чего СЛАУ легко решается.

Метод состоит из двух частей:

1-ая часть – прямой ход: приведение матрицы к треугольному виду.

2-ая часть – обратный ход: решение СЛАУ с треугольной матрицей.

Прямой ход:

1) 2)

………………………………..

……..

Нюансы метода Гаусса:

Если ведущий элемент (на диагонали) на каком либо этапе обратного хода равен нулю – переставим строки (строки смотрим ниже диагонали) так, чтобы ведущий элемент не был равен нулю. Если это не возможно, т.е. в j-ом столбце все строки с i-ой и вниз нулевые, тогда матрица А вырожденная.

2. Модификация метода Гаусса:

Метод Гаусса с выбранным ведущим элементом.

Единственное отличие модифицированного метода Гаусса от обычного состоит в том, что на каждом этапе прямого хода на место ведущего элемента ставим максимальный по модулю среди возможных, т.е среди элементов столбца, который находится не выше главной диагонали.

Пример решения СЛАУ модифицированным методом Гаусса:

1) 2) 3) 4)

(на втором этапе выбираем максимальный по модулю элемент и меняем строку, содержащую выбранный элемент с первой строкой)

Замечания: метод Гаусса с выбором ведущего элемента работает лучше (точнее) чем обычный метод Гаусса (т.е. его точность выше). Погрешности при реализации метода Гаусса возникают при машинном округлении чисел, модифицированный метод Гаусса позволяет решать с той же точностью.

3. Трудоемкость метода Гаусса:

Прямой ход: три цикла

j от 1 до n-1 - по столбцу

i от j+1 до n - по строке

k от j+1 до n+1

Обратный ход: два цикла

П.2 Приближенные методы решения СЛАУ:

§ В приближенных методах точные решения получаются как предел бесконечной последовательности приближений, который мы в некоторый момент времени обрываем (когда достигается заданная точность).

1.Справочный материал. Нормы векторов и матриц:

Пусть х – n-мерный вектор.

Нормой вектора называется число, удовлетворяющее следующим свойствам (аксиомам и нормам):

1) 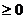, =0 x=0 - Норма неотрицательна и равна нулю когда вектор равен нулю.

Замечания:

а) Фактически норма вектора есть ни что иное, как его длина.

б) Мы живем в пространстве с нормой 2, но на практике обычно удобнее использовать 1-ую или бесконечную нормы.

Примеры норм: x = ()

§ - первая норма

§ - вторая норма

§ - бесконечная норма

Определение: Нормой матрицы А называется число, которое определяется таким образом:

Теорема 2.1:

Норма произведения не превосходит произведения норм.

Доказательство: y

Имеем:

Следствие 2.2:

Норма k-ой степени

Следующая цель – эффективно научиться считать нормы матрицы.

Теорема 2.3:

Легко вычисляются

по опр. по теореме 2.3

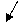
(2.1)

максимальная сумма модулей элементов матрицы по столбцам.

(2.2)

максимальная сумма модулей элементов матрицы по строкам.

Доказательство 2.2:

Итак, мы доказали неравенство

для полного доказательства теоремы необходимо доказать второе неравенство (для этого достаточно определить вектор , которого выполняется (*)).

если для некоторого вектора выполняется такое равенство, то:

для окончательного доказательства остается определить вектор , для которого выполняется искомое равенство (*).

Для того чтобы определить искомый вектор со свойством (*), рассмотрим ту строку матрицы, в которой достигается максимальная сумма модулей элементов. Пусть это строка с номером 0.

тогда положим соответствующую координату

Тогда координата с номером 0 получается умножением на столбец.

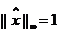, с учетом этого факта получили искомое соотношение (*), что и доказывает теорема 2.3.

2.Метод простых итераций (МПИ):

Пусть дана СЛАУ с квадратной невырожденной матрицей А, проделаем с ней следующие преобразования: поделим каждую строку матрицы на диагональный элемент (предполагается что все элементы не нулевые). Данное преобразование называется приведением матрицы к виду удобному для итерации.

После данных преобразований по диагонали получаются единицы:

(.... – какие то произвольные элементы, получившиеся путем преобразования исходных, по выше описанному способу)

разобьем матрицу А на сумму матриц Е и С, где матрица Е – единичная матрица и матрица С – по диагонали нули.

А=Е+С

С=

Е=

(где элементы матрицы С: - и есть элементы матрицы А)

Исходное СЛАУ преобразовано таким образом:

Ax=b (E+C)=b

x+Cx=b x=b-Cx (2.3)

СЛАУ приведенное к виду удобному для итераций.

Рассмотрим итерационный процесс (2.4)

Из вектора 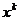- получаем следующий вектор .

Стартовый вектор 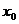- обычный нулевой вектор.

Теорема 2.4:

Если итерационный процесс (2.4) сходится, то есть существует

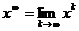, то этот предельный вектор 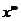и будет точным решением исходного

СЛАУ (2.3)

Доказательство:

Рассмотрим формулу (2.4)

Необходимо исследовать важный вопрос: когда итерационный процесс (2.4) – сходится?

Ответ дает теорема 2.5

Теорема 2.5(достаточное условие сходимости):

Если ||C||<1, то итерационный процесс 2.4 сходится, и скорость его сходимости – геометрическая прогрессия со значением ||C||.

Доказательство:

Для того чтобы доказать, что данная последовательность сходится, докажем, что норма разности , считаем, что k>l

0 0

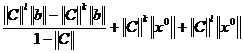(2.5)

Следствие 2.6:

Если , то - точное решение исходного СЛАУ (сходится со скоростью геометрической прогрессии со знаменателем ), а именно, если взять стартовый вектор . (2.6)

Следствие 2.7 (оценка необходимого числа шагов для достижения заданной точности):

Если заданна дополнительная погрешность , то, сделав N шагов, мы получим решение с заданной точностью, т. е.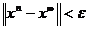

точное

Доказательство:

Решаем неравенство из формулы (2.6):

; ;

Пример СЛАУ, решенной МПИ:

Матрица А имеет вид:

:5 (приводим к виду удобному для итераций - делим каждую

:(-3) строку матрицы так, чтобы получить единицы по главной

:4 диагонали)

Получаем матрицу:

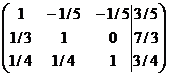
Разбиваем матрицу А на сумму матриц Е и С:

А=Е+С:

Первый шаг по МПИ (начальный вектор X - нулевой):

Второй шаг МПИ:

………………….

количество шагов

Замечание 2.8:

Заметим, что условие для матрицы С, полученной из матрицы А с помощью стандартной процедуры приведения к виду удобному для итераций, равносильно тому, что для исходной матрицы А выполняется условие диагонального преобразования по строкам, т.е. в каждой строке диагональный элемент строго больше суммы модулей.

Доказательство:

Заметим, что:

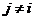
, j = i

, ;