Частотные функции и характеристики

 

Важнейшей характеристикой динамического звена является его частотная передаточная функция. Частотная передаточная функция легко получается из обычной передаточной функции подстановкой , т.е.

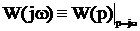                             (8)

Частотная передаточная функция  представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной. Частотная передаточная функция может быть представлена в виде:

,           (9)

здесь

     – амплитудная частотная характеристика (АЧХ);

    – фазовая частотная характеристика (ФЧХ);

    – вещественная частотная характеристика (ВЧХ);

     – мнимая частотная характеристика (МЧХ).

На комплексной плоскости частотная передаточная функция определяет вектор, длина которого равна , а аргумент равен углу , образованному этим вектором с положительной действительной полуосью, что видно по рисунку 4. Годограф этого вектора, т.е. кривую, описываемую концом вектора  при изменении частоты от 0 до ∞ или от -∞ до +∞, называют амплитудно-фазовой частотной характеристикой (АФХ) или годографом Найквиста.

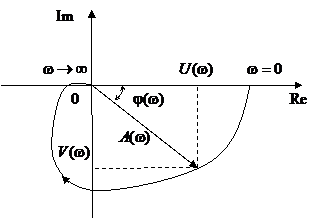
Рисунок 4 - Амплитудно-фазовая частотная характеристика

 

Для нахождения вещественной и мнимой частей частотной передаточной функции часто бывает необходимо освободиться от мнимой части в ее знаменателе. Для этого следует ее числитель и знаменатель умножить на сопряженный знаменателю множитель. Например, если

,

то

В общем случае амплитудная частотная характеристика имеет вид:

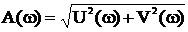,                        (10)

а фазовая частотная характеристика:

(11)

При построении частотных характеристик систем, состоящих из нескольких соединенных типовых звеньев, удобно пользоваться следующими правилами вычисления модуля и аргумента комплексных функций [1]:

1 модуль произведения комплексных чисел равен произведению модулей сомножителей:

,                          (12)

а аргумент – сумме аргументов сомножителей:

.                       (13)

2 модуль дроби комплексных чисел  равен дроби модулей:

,                                     (14)

а аргумент – разности аргументов числителя и знаменателя:

.                        (15)

При исследовании систем управления амплитудную и фазовую характеристики удобно строить в логарифмических координатах. При этом построение точных графиков логарифмических функций даже типовых звеньев требует достаточно трудоемких вычислений, поэтому на практике удобно пользоваться приближенными асимптотическими логарифмическими характеристиками.

Прологарифмируем выражение (9):

.                       (16)

Из выражения (16) видно, что первое слагаемое определяет логарифмическую амплитудную частотную характеристику (ЛАЧХ), а второе – логарифмическую фазовую частотную характеристику (ЛФЧХ). ЛАЧХ строится в виде зависимости 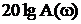 от , а ЛФЧХ в виде зависимости  от .

Использование логарифмических характеристик позволяет достаточно просто строить частотные характеристики системы, состоящей из нескольких звеньев, т.к. если прологарифмировать выражение (12) мы получим, что логарифм модуля произведения равен сумме логарифмов модулей сомножителей:

.                                   (17)

Фазовая частотная характеристика строится в логарифмическом масштабе только по оси абсцисс, т.е. фазовый сдвиг цепочки звеньев и так получается просто в виде суммы фазовых сдвигов на отдельных звеньях, что видно из выражения (13).

На оси частот обычно указывают либо значение , тогда единицей приращения является одна декада, либо значение самой частоты .

Опр. 5: Интервал частот, отличающихся друг от друга в 10 раз называют декадой и обычно принимают за единицу логарифмического масштаба [2].

Как было отмечено ранее, для построения ЛАЧХ находится величина 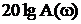, которая обозначается и выражается в децибелах. Децибел равен одной десятой бела.

Опр.6: Бел – логарифмическая единица, которая соответствует десятикратному увеличению мощности, т.е. 1 бел соответствует усиления мощности в 10 раз, 2 бела – в 100 раз и т.д. [2].

Проиллюстрируем порядок построения асимптотической ЛАЧХ на примере апериодического звена первого порядка с передаточной функцией:

.

Запишем частотную передаточную функцию звена:

.

Выделив реальную и мнимую части частотной передаточной функции, получим выражения для амплитудной и фазовой частотных характеристик:

Прологарифмируем выражение для амплитудной частотной характеристики:

.

Для простоты построения при  пренебрегают слагаемым  под корнем, т.к. оно меньше единицы, а при  - единицей. Тогда выражение для асимптотической ЛАЧХ апериодического звена можно записать в виде:

Опр. 7: Частоты, на которых асимптотические ЛАЧХ претерпевают излом, называются сопрягающими частотами [1].

Для построения асимптотической ЛАЧХ системы с произвольной передаточной функцией необходимо предварительно записать ее в следующем виде:

,                            (18)

где  - общий коэффициент усиления системы;

 - порядок астатизма системы, который определяется числом идеальных интегрирующих звеньев в системе;

 - передаточная функция типового звена с единичным коэффициентом усиления, а  - число типовых звеньев.

Правило построения асимптотических ЛАЧХ:

1 записать передаточную функцию системы в виде соединения типовых звеньев согласно выражению(18);

2 вычислить величину начального усиления равную ;

3 определить все сопрягающие частоты и последовательно пронумеровать их;

4 отметить все сопрягающие частоты на оси абсцисс;

5 отметить точку (; ) на координатной плоскости;

6 через отмеченную точку провести первую асимптоту под наклоном - 20 дБ/дек до первой частоты сопряжения;

7 следующая асимптота проводится от конца первой асимптоты до следующей частоты сопряжения под наклоном  дБ/дек, при этом a определяет порядок звена, а знак зависит от того, в числителе или знаменателе соответственно находится множитель, содержащий частоту спряжения на конце данной асимптоты.

8 таким образом строятся последующие асимптоты: i -тая асимптота начинается от сопрягающей частоты 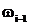 до частоты , при этом наклон определяется частотой .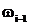

Последняя асимптота представляет собой прямую, которая начинается от частоты  и уходит в бесконечность, при этом ее наклон будет соответствовать выражению  дБ/дек, где d – порядок знаменателя передаточной функции, а b – порядок числителя. Конечный наклон асимптотической ЛАЧХ всегда будет отрицательный, что является следствием из правила физической реализуемости системы

 

Электрические цепи

 

Динамические звенья системы управления могут быть различными по своей физической природе: электрические, механические, гидравлические и т.д. Наиболее просто такие звенья могут быть составлены из электрических R-, C- и L-элементов, модели которых приведены на рисунке 5.

 

а	б	в

Рисунок 5 – Элементы электрических элементов

 

Уравнения электрической цепи составляются на основе законов Кирхгофа, представляющих собой условия непрерывности токов и равновесия напряжений:

1 сумма токов в любом узле равна нулю;

2 сумма напряжений в любом контуре равна нулю.

Уравнения электрической цепи:

- уравнение активного сопротивления R:

;                                    (19)

- уравнение конденсатора С:

                           (20)

где  – ток, протекающий через конденсатор;

- уравнение катушки L:

,                                  (21)

где  – ток, протекающий через конденсатор.

 

Пример выполнения работы

На рисунке 6 приведена электрическая схема типового звена, где R =1.6 кОм, а C = 2 мкФ.

Рисунок 6 – Электрическая схема

 

Для заданной электрической схемы необходимо:

1 составить дифференциальное уравнение;

2 записать передаточную функцию;

3 определить по полученной передаточной функции тип звена или соединения звеньев;

4 найти выражения для построения временных характеристик, привести таблицы значений, построить временные характеристики;

5 найти выражения для построения частотных характеристик (АЧХ, ФЧХ, АФХ, ЛАЧХ, ЛФЧХ), привести таблицы значений, построить частотные характеристики.

 

Решение.

В соответствии с первым законом Кирхгофа имеем:

.

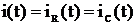Второй закон для единственного контура запишется как:

.

Согласно выражениям (19) и (20) запишем:

.

Напряжение на конденсаторе  является выходным напряжением, т.е. . Тогда, на основании полученных соотношений, запишем:

,

где  - оператор дифференцирования.

Разделив выходное напряжение на входное мы получим выражение для передаточной функции звена:

, где .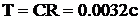

Итак, по виду передаточной функции можно сделать вывод, что была приведена электрическая схема апериодического звена первого порядка.

Для нахождения переходной функции воспользуемся выражением (5).

Для того чтобы найти оригинал  необходимо выражение для изображения  разбить на элементарные дроби и по таблице изображений Лапласа (приложение А) найти оригиналы элементарных дробей.

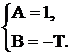
Тогда выражение для переходной функции будет иметь вид:

.

Из полученного выражения для переходной функции в соответствии с выражением (7) получим:

.

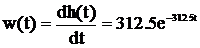Составим таблицу значений и построим по ней временные характеристики звена.

 

0	0	312,5
0,001	0,268384371	228,6299
0,005	0,790388613	65,50356
0,01	0,956063066	13,73029
0,02	0,998069546	0,603267
0,1	1	8,38E-12
10	1	0

 

а	б

Рисунок 7 – Временные характеристики апериодического звена

 

Выражение для частотной передаточной функции:

.

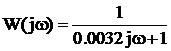Для нахождения выражения для АЧХ и ФЧХ необходимо выделить реальную и мнимую части частотной передаточной функции:

Согласно выражениям (10) и (11)

,

.

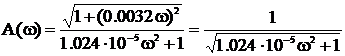Составим таблицу значений и построим по ней частотные характеристики звена.

 

0	1	0
0,001	0,952424	-0,00018
0,01	0,298275	-0,00183
0,1	0,031235	-0,01833
0,2	0,015623	-0,03667
0,5	0,00625	-0,09167
1	0,003125	-0,18335
10	0,000312	-1,83284
100	3,12E-05	-17,7447
1000	3,12E-06	-72,646
10000	3,12E-07	-88,2101
1000000	3,13E-09	-89,9821

 

а	б

Рисунок 8 – Частотные характеристики апериодического звена

 

Рисунок 9 – Амплитудно-фазовая характеристика звена

 

Для построения ЛАЧХ необходимо определить следующие параметры:

 дБ, =0,  с^-1.

Рисунок 10 – Логарифмические частотные характеристики апериодического звена