При переносе узла через сумматор необходимо добавлять элемент сравнения (рисунок 7 а), а при переносе сумматора через узел – сумматор (рисунок 7 б).
| а | 
|
| б | 
|
Рисунок 7 – Перенос узла через сумматор и сумматора через узел
При эквивалентных преобразованиях одной и той же структурной схему могут быть получены различные передаточные функции по разным входам и выходам. Чаще всего при исследовании систем используются передаточные функции по управляющему 
и возмущающему 
воздействию. Обозначаются такие передаточные функции с указанием учитываемого входного и выходного сигнала, 
и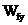 
соответственно.
Рисунок 8– Структурная схема системы с управляющим и возмущающим воздействием
При вычислении передаточной функции по управляющему воздействию полагают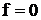 
. Тогда для одноконтурной системы, структурная схема которой приведена на рисунке 8, получим:
.
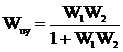При вычислении передаточной функции по возмущающему воздействию полагают 
. Тогда передаточная функция системы по возмущающему воздействию будет иметь вид:
.
Возможно также нахождения передаточных функций по ошибке, т.е. по выходу e, передаточные функции при этом записываются как 
и 
.
Метод Мейсона
Граф прохождения сигнала, или сигнальный граф, разработал Мейсон для наглядного представления и описания связей в системе [1,3]. Граф удобен тем, что он позволяет вычислять передаточные функции многоконтурных систем без предварительного преобразования их структурных схем.
Опр. 9: Графом называется совокупность множества V точек, называемых вершинами, и множества R простых (т.е. самонепересекающихся) кривых, называемых ребрами, удовлетворяющих следующим условиям:
1) каждое незамкнутое ребро содержит ровно две точки множества V, которые являются граничными точками ребра;
2) каждое замкнутое ребро содержит только одну точку из V (граничные точки совпадают);
3) ребра не имеют общих точек, за исключением точек из множества V.
При построении графа системы управления по ее структурной схеме нужно исходную схему представить так, чтобы в сумматорах все переменные складывались с положительным знаком. Далее руководствуются следующими правилами:
1) каждый сумматор заменяется вершиной, которой ставится в соответствие выходная переменная заменяемого сумматора;
2) каждое звено заменяется дугой с оператором, равным оператору заменяемого звена; если выходная переменная подается на сумматор с отрицательным знаком, то оператор дуги записывается с противоположным знаком;
3) каждой переменной соответствует своя вершина.
Пример построения графа управления по заданной структурной схеме приведен на рисунке 9.
Рисунок 9 – Построение графа системы управления
Дадим определение основным компонентам графа управления [4]:
Узел-источник – это узел, из которого сигналы только вытекают.
Узел-сток – это узел, в который все сигналы только втекают.
Путь – это непрерывная последовательность ветвей от узла к узлу, причем стрелки на всех ветвях направлены в одну сторону, т.е. сигналы распространяются в одном направлении.
Контур – это замкнутый путь, в котором стрелки на всех ветвях направлены в одну сторону и каждый узел встречается не более одного раза.
Прямой путь – это путь от узла-источника к узлу-стоку, в котором ни один узел не встречается более одного раза.
Коэффициент передачи пути/контура – произведение передаточных функций всех ветвей, образующих путь/контур.
Несоприкасающиеся контуры – контуры, не имеющие общих узлов.
Используя данные определения, приведем формулу Мейсона, по которой определяется передаточная функция от узла-источника к узлу-стоку:
, (5)
где 
- коэффициент передачи прямого пути;
p – число прямых путей;
- определитель подграфа, получающийся из исходного графа при удалении дуг и вершин k-го простого пути;
- определитель графа:
, (6)
где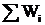 
- сумма коэффициентов передачи всех контуров;
и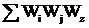 
- сумма произведений двух, трех и т.д. коэффициентов передачи контуров, не соприкасающихся друг с другом.
Порядок вычисления передаточной функции системы методом Мейсона следующий:
1) построить граф системы управления по заданной структурной схеме;
2) записать коэффициенты передачи всех контуров, определить пары, тройки и т.д. несоприкасающихся контуров;
3) по формуле (6) записать определитель графа системы;
4) записать все прямые пути графа, определители подграфов;
5) вычислить передаточную функцию системы по формуле (5).
Пример выполнения работы
Структурная схема системы управления представлена на рисунке 10. По заданной структурной схеме получим передаточную функцию системы по управляющему воздействию:
- методом прогонки сигнала;
- методом структурных преобразований;
- методом Мейсона.
Рисунок 10 – Структурная схема системы управления
Решение.
1 Запишем систему уравнений для всех звеньев системы (рисунок 10):
Будем последовательно подставлять выражения для проходящих сигналов системы в уравнение для выходного сигнала:
В результате подобных упрощений мы должны исключить все промежуточные сигналы, т.е. в уравнении должны остаться только сигналы и 
, и передаточные функции перед ними. Поэтому в полученном выражении будем дальше подставлять уравнение вместо сигнала 
, а выражение с выходным сигналом оставим неизменным.
В полученном уравнении осталось исключить только сигнал 
. Преобразуем выражение с сигналом отдельно:
Ранее мы получали, что 
, тогда 
. Подставим в уравнение, записанное выше, полученное выражение вместо сигнала 
:
Тогда итоговое уравнение относительно u и y примет вид:
Если перенести выражение с в левую часть уравнения, а выражение с оставить справа, то, разделив выходной сигнал на входной, мы можем записать передаточную функцию исходной системы:
2 Заданная система управления является многоконтурной с перекрестными связями. Для того, чтобы избавиться от перекрестных связей по правилам эквивалентных преобразований объединим два элемента сравнения (рисунок 11), находящихся перед входом звена с передаточной функцией 
, перенесем узел со входа звена с передаточной функцией 
на выход. Так же заменим два параллельно соединенных звена с передаточными функциями 
и 
одним звеном с эквивалентной передаточной функцией 
.
Рисунок 11– Первый этап преобразования структурной схемы
Для дальнейшего преобразования необходимо звенья, соединенные последовательно и охваченные обратной связью, заменить звеном с эквивалентной передаточной функцией, как это показано на рисунке 12.
Рисунок 12–Второй этап преобразования структурной схемы
Теперь можно записать выражение передаточной функции для полученной одноконтурной структурной схемы:
Итак, передаточная функция системы по управляющему воздействию имеет вид:
3 Для вывода передаточной функции системы с использованием формулы Мейсона необходимо по заданной структурной схеме системы построить граф системы. Граф исходной системы управления приведен на рисунке 13.
Рисунок 13 – Граф системы управления
Заменим дуги с коэффициентами передачи 
и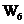 
одной дугой с коэффициентом передачи . Результат такого преобразования приведен на рисунке 14.
Рисунок 14 – Преобразованный граф системы
Для того чтобы воспользоваться формулой Мейсона, запишем сначала коэффициенты передачи всех контуров:
.
Контуры 
и 
несоприкасающиеся. Тогда можно записать определитель графа:
Запишем все прямые пути графа:
Определитель подграфа при исключении пути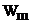 
будет 
.
Тогда по формуле Мейсона получим выражение для передаточной функции системы:
Итак, в результате выполнения задания тремя различными методами по заданной структурной схеме была выведена передаточная функция системы управления по управляющему воздействию. Очевидно, что во всех трех случаях выражения для передаточной функции системы получились одинаковыми.
