Графический пользовательский интерфейс

Отображение информации

Проблема представления накопленной информации (например, данных о климатических изменениях за продолжительный период, о динамике популяций животного мира, об экологическом состоянии различных регионов и т.п.) лучше всего может быть решена посредством графического отображения.

Ни одна из областей современной науки не обходится без графического представления информации. Помимо визуализации результатов экспериментов и анализа данных натурных наблюдений существует обширная область математического моделирования процессов и явлений, которая просто немыслима без графического вывода. Например, описать процессы, протекающие в атмосфере или океане, без соответствующих наглядных картин течений или полей температуры практически невозможно. В геологии в результате обработки трехмерных натурных данных можно получить геометрию пластов, залегающих на большой глубине.

В медицине в настоящее время широко используются методы диагностики, использующие компьютерную визуализацию внутренних органов человека. Томография (в частности, ультразвуковое исследование) позволяет получить трехмерную информацию, которая затем подвергается математической обработке и выводится на экран. Помимо этого применяется и двумерная графика: энцефалограммы, миограммы, выводимые на экран компьютера или графопостроитель.

Проектирование

В строительстве и технике чертежи давно представляют собой основу проектирования новых сооружений или изделий. Процесс проектирования с необходимостью является итеративным, т.е. конструктор перебирает множество вариантов с целью выбора оптимального по каким-либо параметрам. Не последнюю роль в этом играют требования заказчика, который не всегда четко представляет себе конечную цель и технические возможности. Построение предварительных макетов - достаточно долгое и дорогое дело. Сегодня существуют развитые программные средства автоматизации проектно-конструкторских работ (САПР), позволяющие быстро создавать чертежи объектов, выполнять прочностные расчеты и т.п. Они дают возможность не только изобразить проекции изделия, но и рассмотреть его в объемном виде с различных сторон. Такие средства также чрезвычайно полезны для дизайнеров интерьера, ландшафта.

Моделирование

Под моделированием в данном случае понимается имитация различного рода ситуаций, возникающих, например, при полете самолета или космического аппарата, движении автомобиля и т.п. В английском языке это лучше всего передается термином simulation. Но моделирование используется не только при создании различного рода тренажеров. В телевизионной рекламе, в научно-популярных и других фильмах теперь синтезируются движущиеся объекты, визуально мало уступающие тем, которые могут быть получены с помощью кинокамеры. Кроме того, компьютерная графика предоставила киноиндустрии возможности создания спецэффектов, которые в прежние годы были попросту невозможны. В последние годы широко распространилась еще одна сфера применения компьютерной графики - создание виртуальной реальности.

Графический пользовательский интерфейс

На раннем этапе использования дисплеев как одного из устройств компьютерного вывода информации диалог "человек-компьютер" в основном осуществлялся в алфавитно-цифровом виде. Теперь же практически все системы программирования применяют графический интерфейс. Особенно впечатляюще выглядят разработки в области сети Internet. Существует множество различных программ-браузеров, реализующих в том или ином виде средства общения в сети, без которых доступ к ней трудно себе представить. Эти программы работают в различных операционных средах, но реализуют, по существу, одни и те же функции, включающие окна, баннеры, анимацию и т.д.

В современной компьютерной графике можно выделить следующие основные направления: изобразительная компьютерная графика, обработка и анализ изображений, анализ сцен (перцептивная компьютерная графика), компьютерная графика для научных абстракций (когнитивная компьютерная графика, т.е. графика, способствующая познанию).

Изобразительная компьютерная графика своим предметом имеет синтезированные изображения. Основные виды задач, которые она решает, сводятся к следующим:

• построение модели объекта и формирование изображения;
• преобразование модели и изображения;
• идентификация объекта и получение требуемой информации.

Обработка и анализ изображений касаются в основном дискретного (цифрового) представления фотографий и других изображений. Средства компьютерной графики здесь используются для:

• повышения качества изображения;
• оценки изображения - определения формы, местоположения, размеров и других параметров требуемых объектов;
• распознавания образов - выделения и классификации свойств объектов (при обработке аэрокосмических снимков, вводе чертежей, в системах навигации, обнаружения и наведения).

Анализ сцен связан с исследованием абстрактных моделей графических объектов и взаимосвязей между ними. Объекты могут быть как синтезированными, так и выделенными на фотоснимках. К таким задачам относятся, например, моделирование "машинного зрения" (роботы), анализ рентгеновских снимков с выделением и отслеживанием интересующего объекта (внутреннего органа), разработка систем видеонаблюдения.

Когнитивная компьютерная графика - только формирующееся новое направление, пока еще недостаточно четко очерченное. Это - компьютерная графика для научных абстракций, способствующая рождению нового научного знания. Технической основой для нее являются мощные ЭВМ и высокопроизводительные средства визуализации.

Одним из наиболее ранних примеров использования когнитивной компьютерной графики является работа Ч.Страуса "Неожиданное применение ЭВМ в чистой математике" (ТИИЭР, т. 62, № 4, 1974, с.96-99). В ней показано, как для анализа сложных алгебраических кривых используется "n-мерная" доска на основе графического терминала. Пользуясь устройствами ввода, математик может легко получать геометрические изображения результатов направленного изменения параметров исследуемой зависимости. Он может также легко управлять текущими значениями параметров, "углубляя тем самым свое понимание роли вариаций этих параметров". В результате получено "несколько новых теорем и определены направления дальнейших исследований".

В настоящем курсе предполагается рассмотреть следующие вопросы:

• представление изображения в компьютерной графике;
• способы подготовки изображения к визуализации;
• методы вывода изображения на экран;
• методы работы с изображением;
• методы вычислительной геометрии.

2,Компьютерная геометрия в векторной графике. Построение линий. Однородные координаты. Матричные преобразования. Кривые Безье, NURBS.

Векторная компьютерная графика имеет на сегодняшний день очень широкую область применения в самых различных областях человеческой деятельности, начиная от рекламы на страницах газеты и заканчивая разработкой проектов в таком виде промышленности как космическая.

Векторное изображение изначально позволяет выполнять точные геометрические построения, следовательно, чертежи и другую конструкторскую документацию. Заметим, что почти все системы автоматизированного проектирования в свою основу берут векторную компьютерную графику. Надо ли говорить, что векторная компьютерная графика наряду с растровой широко применяется художниками-дизайнерами и связанно это в первую очередь с особенностями этого вида компьютерной графики.

Векторное изображение (векторная графика) представляется в виде совокупности отрезков прямых (векторов), а не точек, которые применяются в растровых изображениях. Векторная графика описывает изображения с использованием прямых и изогнутых линий, называемых векторами, а также параметров, описывающих цвета и расположение.

Например, изображение описывается точками, через которые проходит линия, создавая тем самым контур. Цвет задается цветом контура и области внутри этого контура. Остановимся на описании отличительных особенностей векторных и растровых изображений - объектов. Каждое такое изображение может состоять из одного или нескольких графических объектов соответствующего типа.

Векторный графический объект включает два элемента: контур и его внутреннюю область, которая может быть пустой или иметь заливку в виде цвета, цветового перехода (градиента), или мозаичного рисунка. Контур может быть как замкнутым, так и разомкнутым. В векторном объекте он выполняет двойную функцию. Во-первых, с помощью контура можно менять форму объекта. Во-вторых, контур векторного объекта можно оформлять (тогда он будет играть роль обводки), предварительно задав его цвет, толщину и стиль линии.

Под стилем оформления линии подразумевается набор штрихов и полосок, из которых она состоит, а также параметры этой линии в точках перегиба и на концах. Любое векторное изображение можно представить в виде набора векторных объектов, расположенных определенным образом друг относительно друга. Векторное изображение можно сравнить с аппликацией, состоящей из кусочков цветной бумаги, наклеенных (наложенных) один на другой. Однако, в отличие от аппликации, в векторном изображении легко менять форму и цвет составных частей.

Таким образом, векторная графика в основном «живет» созданием новых объектов, широко используется в дизайнерских проектах, в то время как растровая графика изначально создавалась и существует для обработки фотографий, это видно и из самих названий программ – Adobe PHOTOshop, Corel PHOTO-Paint. 

В основе векторной компьютерной графики лежит расчёт координат экранных точек, входящих в состав линии контура изображения, поэтому этот вид компьютерной графики называют вычисляемым. В основе векторной графики лежат математические представления о свойствах геометрических фигур (в основном этот процесс затрагивает расчёты, связанные с представлением линии). Векторная графика использует для построения изображений координатный способ. Основным базовым понятием в векторной компьютерной графике является - линия.

Для её математического представления используются: точка, прямая, отрезок прямой, парабола, отрезок параболы, функция y=x3, кривая второго порядка, кривая третьего порядка, кривая Безье. Соподчинёнными для понятия линия являются: точка, конец кривой линии, управляющая линия касательная к кривой, изгиб кривой, маркер управляющей линии. Также как и линия, основным базовым понятием для векторной графики является объект.

Объектом называется любой графический элемент внутри векторного изображения, состоящий из отрезка прямой или кривой линии или замкнутого контура. При редактировании элементов векторной графики изменяются параметры прямых и изогнутых линий, описывающих форму этих элементов. Можно переносить элементы, менять их размер, форму и цвет, но это не отразится на качестве их визуального представления.

Векторное представление именно и заключается в описании элементов изображения математическими кривыми с указанием их цветов. Еще один пример: красный эллипс на белом фоне будет описан всего двумя математическими формулами - прямоугольника и эллипса соответствующих цветов, размеров и местоположения.

Как следствие, еще одно преимущество - качественное масштабирование в любую сторону. Увеличение или уменьшение объектов производится увеличением или уменьшением соответствующих коэффициентов в математических формулах. Еще один плюс - векторная графика не зависит от разрешения, т.е. может быть показана в разнообразных выходных устройствах с различным разрешением без потери качества.

Но, к сожалению, векторный формат становится невыгодным при передаче изображений с большим количеством оттенков или мелких деталей (например, фотографий). Ведь каждый мельчайший блик в этом случае будет представляться не совокупностью одноцветных точек, а сложнейшей математической формулой или совокупностью графических примитивов, каждый из которых, является формулой. Это приводит к утяжелению файла.

Теперь поговорим о проблеме размеров файлов. Файлы векторных изображений имеют гораздо меньший размер, чем растровых, так как в памяти компьютера каждый из объектов этой графики сохраняется в виде математических уравнений, в то время как параметры каждой точки (координаты, интенсивность, цвет) описываются в файле растровой графики индивидуально, отсюда – такие огромные размеры файлов. Наиболее популярными графическими программами, предназначенными для обработки векторных изображении, являются Adobe Illustrator и Corel DRAW.

Чем же интересно векторное изображение, используемое в компьютерной графике?

Во-первых, с помощью векторной графики можно решить много художественно-графических задач. Во-вторых, возможность масштабирования векторного изображения без потери качества может быть ценна, например, при создании большой по размеру рекламы. Увеличение или уменьшение объекта производится увеличением или уменьшением соответствующих коэффициентов в математических формулах, так как любое векторное изображение можно представить в виде набора векторных объектов, расположенных определенным образом друг относительно друга.

Возможность масштабирования векторного изображения без потери его качества может быть очень ценна, например, для создания учебных плакатов. Векторная компьютерная графика является объектно-ориентированной, т.е. каждый элемент изображения является отдельным объектом, которому можно изменить контур, заливку, пропорции. Это ее свойство может быть использовано, например, при изучении законов композиции: ритма, поиска сюжетно-композиционного центра, симметрии и асимметрии, параллельности в композиции, и пр.

Возможность простого редактирования контура может быть применима для работы над линейным рисунком, дизайном изделий из стекла, керамики и других пластичных материалов. Для декоративно-прикладного искусства векторная компьютерная графика позволяет работать над орнаментальной композицией в круге, квадрате или полосе. Разработав рапорт или элемент орнамента, векторная графика позволяет размножить его без дополнительной прорисовки, что особенно ценно в процессе творческого поиска.

Изначально этот вид компьютерной графики позволяет проводить любые геометрические построения. Это свойство необходимо для таких специальных дисциплин, как техническая графика. С помощью инструментария векторной компьютерной графики можно изучать все разделы черчения и начертательной геометрии. Используя системы автоматизированного проектирования, в основу которых положена векторная компьютерная графика, можно выполнять конструкторскую документацию любого уровня сложности. Типичным примером такой системы является пакет программ AutoCAD. К средствам работы с векторной графикой, которые могут быть использованы для поддержки графических дисциплин, относят такие графические редакторы как Corel Draw, Macromedia Freehand, Adobe illustrator, AutoCAD, ArhiCAD.

Однородным представлением n-мерного объекта в математике, в общем случае, называют его представление в (n+1)-мерном пространстве, полученное добавлением еще одной координаты – скалярного множителя. Однородные координаты на плоскости определяются следующим образом. Пусть на плоскости в аффинной системе координат задана точка P с координатами (x, y). Однородными координатами этой точки называется любая тройка одновременно не равных нулю чисел [w1 w2 w3], связанных с координатами точки Pсоотношениями:

Безразмерное число w3 называется скалярным множителем.

Геометрически можно пояснить однородные координаты точки на плоскости, представив точку в некоторой условной пространственной системе координат (x,y,w), как это показано на рисунке 3.

Точку P(x,y) может представлять тройкой своих координат w1, w2, w3 произвольная точка на прямой, соединяющей начало координат О (0, 0, 0) с точкой P¢ (x, y, 1). В частности, и точка P¢ однозначно определяет точку P, а также и любая точка P¢¢ c координатами (xh, yh, h), где h – скалярный множитель. В этом можно убедиться, воспользовавшись выражениями (2.3). Такое описание точки на плоскости называется в компьютерной графике описанием в однородных координатах. Представляют точку обычно так: (x: y: 1), то есть принимают h=1, но применяют и общую форму: (w1: w2: w3). Чтобы отличить однородное описание точки на плоскости (три координаты – w1, w2, w3) от привычного описания точки в декартовом пространстве (тоже три координаты – x, y, z), однородные координаты в описании точки разделяют не запятой, а двоеточием, например, A(xA:yA:1). Это правило не относится к матричному описанию точки, так как в математике знаки препинания между элементами матриц не ставятся, например, KA =| xA yA 1|.

Теперь аффинное преобразование в общем виде будет выглядеть следующим образом:

или K* = K × T, (2.4)

где обозначения очевидны.

Перемножение матриц K и T даст два основных уравнения (2.1) перевода точки из СКО в СКН и верное числовое равенство 1=1. Следовательно, при помощи троек однородных координат и матриц третьего порядка можно описать любое частное аффинное преобразование. Так, матрица преобразований для сдвига (translation – перенос) принимает вид:

Пример 1. Пусть требуется описать поворот точек объекта на угол q вокруг произвольного центра С с координатами xc,yc.

Применить матрицу поворота RT нельзя, так как она описывает поворот относительно начала координат, а в задании требуется повернуть точку вокруг некоторого центра С. Значит, чтобы использовать RT, нужно сначала разместить начало координат СКН в точке С или, что то же самое, переместить точку С в начало СКН. При этом точка объекта (x: y: 1) также изменит свои координаты. Чтобы найти ее координаты после сдвига, используется матрица TR. Теперь можно описывать поворот точки объекта с помощью матрицы RT. Однако предварительный сдвиг исказит результат преобразования поворота. Чтобы этого не произошло, нужно после поворота выполнить обратный сдвиг (возврат) системы координат, чтобы точка С вновь заняла свое место. Вместе с ней изменит свои координаты и повернутая точка объекта. Для нахождения ее новых координат применяется матрица сдвига с обратными значениями смещений по координатным осям. Таким образом, поворот объекта (каждой его точки) вокруг произвольного центра представляется в виде последовательности следующих действий: сдвиг центра вращения в начало СКН, поворот объекта на угол q вокруг начала координат и сдвиг центра вращения в исходное положение.

Произведение (суперпозиция) трех матриц частных аффинных преобразований представляет собой текущую матрицу геометрического преобразования. Она может быть вычислена, подставлена в выражение (2.4) и использована для нахождения координат всех точек графического объекта при его повороте.

Пример 2. Пусть требуется найти точку P*, симметричную точке P относительно некоторого центра С(xc, yc).

В задании требуется выполнить преобразование центральной симметрии (относительно точки), а частное преобразование отражения описывает осевую симметрию (относительно прямой). Однако центральную симметрию можно представить как результат двух последовательных преобразований осевой симметрии: сначала относительно горизонтальной оси, затем – относительно вертикальной. При этом обе оси должны проходить через центр симметрии. Так как матрица RF «работает» только относительно осей, проходящих через начало координат, перед симметрией нужно предусмотреть сдвиг центра С в начало СКН. Очевидно, после преобразований симметрии нужно предусмотреть возврат точки С на свое старое место (еще один сдвиг). В результате для выполнения задания нужно выполнить следующий ряд преобразований:

Две средние матрицы суперпозиции (матрицы симметрии) можно поменять местами, но в остальном последовательность записи матриц имеет принципиальное значение.

Пример 3. Пусть требуется описать поворот точки на угол q вокруг произвольного центра С с координатами xc, yc и последующее двукратное масштабирование результата относительно начала координат.

Очевидно, начальные преобразования в этом случае совпадают с преобразованиями примера 1, матричная запись которых уже получена. Затем к ним нужно добавить масштабирование, которое в суперпозиции матриц учитывается просто: в суперпозицию справа добавляется матрица

Если теперь после описанных преобразований потребуется выполнить еще одно преобразование, например, еще один сдвиг, то его матрица TR3 также записывается в «старую» суперпозицию справа. Таким образом, последовательность запланированных для выполнения задания геометрических преобразований записываются в виде своих матриц слева направо. При этом последовательность матриц строго соответствует последовательности запланированных преобразований.

Внимание! В приведенных примерах координаты точек записываются в виде матриц-строк. Возможна их запись и в виде матриц-столбцов. Она часто применяется в литературе по компьютерной графике. В этом случае все рассмотренные матрицы частных аффинных преобразований заменяются на транспонированные [2]. В матричной записи преобразования, по сравнению с (2.4), матрицы K и T меняются местами, иначе нельзя выполнить их перемножение. Кроме того, матрицы последовательности преобразований, запланированной для выполнения задания, записываются справа налево, то есть суперпозиция матриц «растет» справа налево. Например, матричное описание преобразований для примера 1 выглядит так:

Кривы́е Безье́ или Кривы́е Бернште́йна-Безье́ были разработаны в 60-х годах XX века независимо друг от друга Пьером Безье (Pierre Bézier) из автомобилестроительной компании «Рено» и Полем де Кастельжо (Paul de Faget de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов автомобилей.

Несмотря на то, что открытие де Кастельжо было сделано несколько ранее Безье (1959), его исследования не публиковались и скрывались компанией как производственная тайна до конца 1960-х.

Кривая Безье является частным случаем многочленов Бернштейна, описанных Сергеем Натановичем Бернштейном в 1912 году.

Впервые кривые были представлены широкой публике в 1962 году французским инженером Пьером Безье, который, разработав их независимо от де Кастельжо, использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастельжо назван разработанный им рекурсивный способ определения кривых (алгоритм де Кастельжо).

Впоследствии это открытие стало одним из важнейших инструментов систем автоматизированного проектирования и программ компьютерной графики.

Кривая Безье — параметрическая кривая,

Виды кривых Безье

Линейные кривые

При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P0 и P1 определяют его начало и конец. Кривая задаётся уравнением:

Квадратичные кривые

Квадратичная кривая Безье (n = 2) задаётся тремя опорными точками: P0, P1 и P2.

Квадратичные кривые Безье в составе сплайнов используются для описания формы символов в шрифтах TrueType и в SWF файлах.

Кубические кривые

В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:

.Кубическая кривая Безье

Четыре опорные точки P0, P1, P2 и P3, заданные в 2- или 3-мерном пространстве определяют форму кривой.

Линия берёт начало из точки P0 направляясь к P1 и заканчивается в точке P3 подходя к ней со стороны P2. То есть кривая не проходит через точки P1 и P2, они используются для указания её направления. Длина отрезка между P0 и P1 определяет, как скоро кривая повернёт к P3.

В современных графических системах и форматах, таких как PostScript (а также основанные на нём форматы Adobe Illustrator и Portable Document Format (PDF)), Scalable Vector Graphics (SVG)[1],Metafont, CorelDraw и GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых.

Построение кривых Безье

Линейные кривые

Параметр t в функции, описывающей линейный случай кривой Безье, определяет, где именно на расстоянии от P0 до P1 находится B(t). Например, при t = 0,25 значение функции B(t) соответствует четверти расстояния между точками P0 и P1. Параметр t изменяется от 0 до 1, а B(t) описывает отрезок прямой между точками P0 и P1.

Квадратичные кривые

Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q0 и Q1 из условия, чтобы параметр t изменялся от 0 до 1:

Точка Q0 изменяется от P0 до P1 и описывает линейную кривую Безье.

Точка Q1 изменяется от P1 до P2 и также описывает линейную кривую Безье.

Точка B изменяется от Q0 до Q1 и описывает квадратичную кривую Безье.

Кривые высших степеней

Для построения кривых высших порядков соответственно требуется и больше промежуточных точек. Для кубической кривой это промежуточные точки Q0, Q1 и Q2, описывающие линейные кривые, а также точки R0 и R1, которые описывают квадратичные кривые: более простое уравнение.

Для кривых четвёртой степени это будут точки Q0, Q1, Q2 и Q3, описывающие линейные кривые, R0, R1 и R2, которые описывают квадратичные кривые, а также точки S0 и S1, описывающие кубические кривые Безье:

Построение кривой Безье 4-й степени

Свойства кривой Безье непрерывность заполнения сегмента между начальной и конечной точками;

кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки;

при наличии только двух контрольных точек сегмент представляет собой прямую линию;

прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек;

кривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой;

масштабирование и изменение пропорций кривой Безье не нарушает её стабильности, так как она с математической точки зрения «аффинно инвариантна»;

изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье;

любой частичный отрезок кривой Безье также является кривой Безье;

степень кривой всегда на одну ступень ниже числа контрольных точек. Например, при трех контрольных точках форма кривой — парабола;

окружность не может быть описана параметрическим уравнением кривой Безье;

невозможно создать параллельные кривые Безье, за исключением тривиальных случаев (прямые линии и совпадающие кривые), хотя существуют алгоритмы, строящие приближённую параллельную кривую Безье с приемлемой для практики точностью.

Применение в компьютерной графике

Благодаря простоте задания и манипуляции, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки опорных точек, то не пересекаются и сами кривые), а с другой стороны позволяет осуществлять интуитивно понятное управление параметрами кривой в графическом интерфейсе с помощью её опорных точек. Кроме тогоаффинные преобразования кривой (перенос, масштабирование, вращение и др.) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.

Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, три смежные опорные точки обеих кривых должны лежать на одной прямой. В программах векторной графики наподобие Adobe Illustrator или Inkscape подобные фрагменты известны под названием «путей» (path).

Неоднородный рациональный сплайн Безье, NURBS (англ. Non-uniform rational Bezier spline) — математическая форма, применяемая в компьютерной графике для генерации и представления кривых и поверхностей. Как следует из названия, является частным случаем B-сплайнов, причём, широко распространённым из-за своей стандартизированности и относительной простоты.

3. Двумерное геометрическое моделирование (2D) средствами графических систем (КОМПАС, AutoCAD).

4. Трехмерное геометрическое моделирование (3D). Способы задания поверхностей в векторной графике. Виды трехмерных геометрических моделей и способы их построения.

5. Формирование объемных твердотельных моделей объектов графическими системами (КОМПАС, AutoCAD, K3).

6. Растровая компьютерная графика. Цветовые модели в компьютерной графике.

Растровое изображение — изображение, представляющее собой сетку пикселей — цветных точек (обычно прямоугольных) на мониторе, бумаге и других отображающих устройствах.

Важными характеристиками изображения являются:

Размер изображения в пикселях — может выражаться в виде количества пикселей по ширине и по высоте (800×600px, 1024×768px, 1600×1200px и т. д.) или же в виде общего количества пикселей (так изображение размером 1600×1200px состоит из 1 920 000 точек, то есть примерно 2 мегапикселей);

Количество используемых цветов или глубина цвета (эти характеристики имеют следующую зависимость: , где 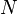— количество цветов, — глубина цвета);

Цветовое пространство (цветовая модель) — RGB, CMYK, XYZ, YCbCr и др.;

Разрешение изображения — величина, определяющая количество точек (элементов растрового изображения) на единицу площади (или единицу длины).

Растровую графику редактируют с помощью растровых графических редакторов. Создаётся растровая графика фотоаппаратами, сканерами, непосредственно в растровом редакторе, а также путём экспорта из векторного редактора или в виде снимков экрана.

Преимущества

Растровая графика позволяет создать практически любой рисунок, вне зависимости от сложности, в отличие, например, от векторной, где невозможно точно передать эффект перехода от одного цвета к другому без потерь в размере файла;

Распространённость — растровая графика используется сейчас практически везде: от маленьких значков до плакатов;

Высокая скорость обработки сложных изображений, если не нужно масштабирование;

Растровое представление изображения естественно для большинства устройств ввода-вывода графической информации, таких как мониторы (за исключением векторных устройств вывода), матричные и струйные принтеры, цифровые фотоаппараты, сканеры, а также сотовые телефоны.

Недостатки

Большой размер файлов у простых изображений;

Невозможность идеального масштабирования;

Невозможность вывода на печать на векторный графопостроитель.

Из‑за этих недостатков для хранения простых рисунков рекомендуют вместо даже сжатой растровой графики использовать векторную графику.

Форматы

Растровые изображения обычно хранятся в сжатом виде. В зависимости от типа сжатия может быть возможно или невозможно восстановить изображение в точности таким, каким оно было до сжатия (сжатие без потерь или сжатие с потерями соответственно). Так же в графическом файле может храниться дополнительная информация: об авторе файла, фотокамере и её настройках, количестве точек на дюйм при печати и др.

Сжатие без потерь

Использует алгоритмы сжатия, основанные на уменьшении избыточности информации.

BMP или Windows Bitmap — обычно используется без сжатия, хотя возможно использование алгоритма RLE.

GIF (Graphics Interchange Format) — устаревающий формат, поддерживающий не более 256 цветов одновременно. Всё ещё популярен из-за поддержки анимации, которая отсутствует в чистом PNG, хотя ПО начинает поддерживать APNG.

PCX — устаревший формат, позволявший хорошо сжимать простые рисованные изображения (при сжатии группы подряд идущих пикселов одинакового цвета заменяются на запись о количестве таких пикселов и их цвете).

PNG (Portable Network Graphics)

Сжатие с потерями

Основано на отбрасывании части информации, как правило наименее воспринимаемой глазом.

JPEG очень широко используемый формат изображений. Сжатие основано на усреднении цвета соседних пикселей(информация о яркости при этом не усредняется) и отбрасывании высокочастотных составляющих в пространственном спектре фрагмента изображения. При детальном рассмотрении сильно сжатого изображения заметно размытие резких границ и характерный муар вблизи них.

Разное

TIFF поддерживает большой диапазон изменения глубины цвета, разные цветовые пространства, разные настройки сжатия (как с потерями, так и без) и др.

Raw хранит информацию, непосредственно получаемую с матрицы цифрового фотоаппарата или аналогичного устройства без применения к ней каких-либо преобразований, а также хранит настройки фотокамеры. Позволяет избежать потери информации при применении к изображению различных преобразований (потеря информации происходит в результате округления и выхода цвета пиксела за пределы допустимых значений). Используется при съёмке в сложных условиях (недостаточная освещённость, невозможность выставить баланс белого и т. п.) для последующей обработки на компьютере (обычно в ручном режиме). Практически все полупрофессиональные и профессиональные цифровые фотоаппараты позволяют сохранять RAW изображения. Формат файла зависит от модели фотоаппарата, единого стандарта не существует.

История

Первые вычислительные машины не имели отдельных средств для работы с графикой, однако уже использовались для получения и обработки изображений. Программируя память первых электронных машин, построенную на основе матрицы ламп, можно было получать узористые картины.

В 1961 году программист С. Рассел возглавил проект по созданию первой компьютерной игры с графикой. Создание игры «Spacewar» («Космические войны») заняло около 200 человеко-часов. Игра была создана на машине PDP-1.

В 1963 году американский учёный Айвен Сазерленд создал программно-аппаратный комплекс Sketchpad, который позволял рисовать точки, линии и окружности на трубке цифровым пером. Поддерживались базовые действия с примитивами: перемещение, копирование и др. По сути, это был первый растровый редактор, реализованный на компьютере. Также программу можно назвать первым графическим интерфейсом, причём она являлась таковой ещё до появления самого термина.

В середине 1960-х гг. появились разработки в промышленных приложениях компьютерной графики. Так, под руководством Т. Мофетта и Н. Тейлора фирма Itek разработала цифровую электронную чертёжную машину. В 1964 году General Motors представила систему автоматизированного проектирования DAC-1, разработанную совместно с IBM.

В 1968 году группой под руководством Константинова Н. Н. была создана компьютерная математическая модель движения кошки. Машина БЭСМ-4, выполняя написанную программу решения дифференциальных уравнений, рисовала мультфильм «Кошечка», который для своего времени являлся прорывом. Для визуализации использовался алфавитно-цифровой принтер. Существенный прогресс компьютерная графика испытала с появлением возможности запоминать изображения и выводить их на компьютерном дисплее.

2. Цветовая модель RGB.

Каждый из цветов R-Красный, G-Зеленый и B-Синий имеют один из 256 уровней интенсивности. Эту систему еще называют аддитивной, потому что с увеличением яркости отдельных цветов результирующий цвет тоже становится ярче.

На рисунке (рис.2) показано, как смешиваются цвета, например красный + зеленый, дает желтый, а красный, + синий, даст фиолетовый. При равной интенсивности всех трех цветов, получаются градации серого, при максимальной яркости – белый, при отсутствии – черный.

С точки зрения редактирования изображения на экране компьютера, эта цветовая модель является наиболее удобной, так как обеспечивает доступ ко всем 16 миллионам цветов, которые могут быть выведены на экран. Недостатком этой системы RGB является то, что не все цвета, созданные в этом режиме могут быть выведены на печать.

3. Цветовая модель CMYK.

CMYK в отличие от RGB является субтрактивной системой, то есть на бумаге, максимальная яркость дает черный цвет, а отсутствие – белый, в этом их принципиальное различие. Раскладывается она тоже по-другому, на С(Cyan – голубой), M(Magenta – пурпурный), Y(Yellow – желтый) и B(blacK – черный). Эта система используется для печати, поэтому если вы на компьютере редактируете изображение в режиме RGB, перед печатью переведите его в режим CMYK.

На рисунке (рис.3) показано, как смешиваются цвета в этой системе. Голубой + пурпурный дают глубокий синий цвет, пурпурный + желтый, дают ярко-красный, желтый + голубой – зеленый. Голубой, пурпурный и желтый образуют грязно-коричневый цвет. Черный делает любой цвет более темным, отсутствие красителя дает белый.

Интересная особенность этой системы в том, что, не смотря на то, что количество каналов у CMYK целых четыре, и каждый из них содержит 256 градация яркости, цветовое пространство CMYK уже, чем у RGB. Типографские краски не могут передать все цвета RGB, поэтому визуально насыщенность CMYK ниже, чем у RGB.

Собственно, для получения полной палитры требуется 3 цвета: С(Cyan – голубой), M(Magenta – пурпурный), Y(Yellow – желтый). Черный (Black) используется для усиления черного, из-за недостаточно качественной накатки полиграфических машин.

Еще один из моментов при работе в этом цветовом режиме такой, для точного соответствия цветового отображения рисунка на мониторе и на бумаге, при печати, необходимо очень хорошо откалибровать монитор, потому, что очень часто, то, что вы сделаете на мониторе, на бумаге будет выглядеть совсем по другому.

4. Цветовая модель HSB.

Следующая система, которая используется в компьютерной графике, система HSB. Растровые форматы не используют систему HSB для хранения изображений, так как она содержит всего 3 миллиона цветов.

В системе HSB (рис. 4) цвет разлагается на три составляющие:

HUE (Цветовой тон) – частота световой волны, отражающейся от объекта, который вы видите.

SATURATION (Насыщенность) является чистотой цвета. Это соотношение основного тона и равного ему по яркости бесцветно серого. Максимально насыщенный цвет не содержит серого вообще. Чем меньше насыщенность цвета, тем он нейтральней, тем труднее однозначно охарактеризовать его.

BRIGHTNESS (Яркость) это общая яркость цвета. Минимальное значение этого параметра превращает любой цвет в черный.

При работе в графических программах с ее помощью очень удобно подбирать цвет, так как представление в этой модели цвета согласуется с его восприятием человеком