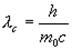Найти: L 2 Р е ш е н и е.

Уровень интенсивности звука в децибелах определяется соотношением:

где J ₀ – условный нулевой уровень интенсивности звука (J ₀ =10^-12 Вт/м²).

При изменении интенсивности звука изменение уровня интенсивности звука будет равно:

Отсюда

Подставляя числовые значения, получим:

   

 

Раздел «Свойства жидкостей»

На тело, погруженное в жидкость, действует выталкивающая сила F, равная весу жидкости, вытесненной телом (закон Архимеда):

,

где -плотность жидкости; g - ускорение свободного падения; V - объем вытесненной жидкости.

Уравнение Бернулли для точек идеальной жидкости, принадлежащих одной линии тока:

,

где р_ст – статическое; - динамическое; -гидростатическое давление; - плотность жидкости; - её скорость; h – высота соответствующей точки жидкости относительно некоторого уровня (например, уровня Земли).

Уравнение Ньютона для вязкой жидкости:

,

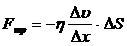где - коэффициент вязкости;  - градиент скорости.

Закон Стокса:

,

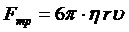где R - радиус шара; - скорость движения шарика в жидкости.

Число Рейнольдса для трубы диаметром D:

,

где 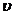- скорость жидкости; 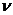- кинематическая вязкость ();  для воды (2000-2400); для крови – (970 80).

Коэффициент поверхностного натяжения:

, или ,

где F -сила поверхностного натяжения; l - длина контура, ограничивающего поверхность жидкости; - измеряется Н/м (или Дж/м²); W - свободная энергия поверхностного слоя жидкости; S - площадь поверхности.

Добавочное (дополнительное) давление (формула Лапласа): ,

где R ₁ и R ₂ – радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости.

Для сферической поверхности , тогда:

,

где - коэффициент поверхностного натяжения жидкости; R - радиус сферической поверхности.

Высота поднятия (опускания) жидкости в капилляре (формула Борелли-Жюрена):

,

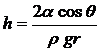где - краевой угол; r- радиус капилляра; - плотность жидкости.

Закон теплопроводности (закон Фурье):

,

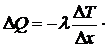
где - коэффициент теплопроводности; - градиент температуры в направлении, перпендикулярном площадке , время .

    Закон диффузии (закон Фика):

,

где D - коэффициент диффузии; 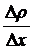- градиент плотности; - площадь площадки; - время.

Относительная влажность воздуха:

или ,

 где абсолютная влажность воздуха; 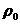- масса пара, необходимая для насыщения 1м³ воздуха при данной температуре,  и  и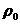змеряется в (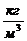); р - парциальное давление; -давление насыщенного пара, измеряются в (Па).

 

Пример № 2

Определить время, в течение которого через поверхность площадью S =1м² продиффундирует воздух массой m =720 мг из почвы в атмосферу, если принять коэффициент диффузии воздуха D =0,04 см²/с, градиент плотности г/см⁴

Дано:

S =1м²

m =720 мг

D =0,04 см²/с

 г/см⁴

Найти: h =?                  Решение:

Масса газа, перенесенная в результате диффузии, выражается формулой Фика

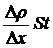, (1)

где D – коэффициент диффузии;  - градиент плотности, т. е. изменение плотности, приходящееся на единицу глубины слоя почвы; S – площадь поверхности почвы; t – длительность диффузии.

Из (1) найдем

(2)

Выразим числовые значения всех величин, входящих в формулу (2), в единицах СИ: m =720мг=7,20 × 10^-4кг.

                             D =0,04см²/с=4 × 10^-6м²/с,

=-0,50 × 10^-6г/см⁴=-0,05 кг/м⁴, S =1м².

  Вычислим длительность диффузии

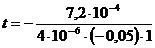с = 3,60 × 10³ с = 1 ч.

Пример № 3

Определить коэффициент теплопроводности тазовой кости лошади, если через площадку этой кости размером 3 ´ 3 см и толщиной 5 мм за час проходит 68 Дж теплоты. Разность температур между внешней и внутренней поверхностями кости в теле лошади составляет 1 °.

Дано:

Q = 68 Дж

D x = 5 мм = 5,005 м

D T = 1 К

t = 1 ч = 3600 c

S = 9 см² = 9 × 10^-4м²

    Найти: λ =?               Решение:

Считая (что не совсем точно), что для данного случая можно применить закон теплопроводности Фурье, напишем:

. Отсюда

Подставляем числовые значения:

Пример № 4.

Определить, при каком градиенте плотности углекислого газа через каждый квадратный метр поверхности почвы продиффундирует в атмосферу в течение 1 ч масса газа мг, если коэффициент диффузии см²/с.

Решение. Масса газа, переносимая в результате диффузии, определяется законом Фика:

                                  ,                                   (1)

где D – коэффициент диффузии;  – градиент плотности, т.е. изменение плотности, приходящееся на 1 м толщины слоя почвы; S – площадь поверхности слоя; t – длительность диффузии.

Из (1) выразим искомый градиент плотности:

                                        .                                 (2)

Вычислим градиент плотности:

кг/м⁴= –0,05кг/м⁴.

Отрицательное значение градиента плотности соответствует сущности процесса диффузии: зависимость плотности от расстояния в направлении движения диффундирующей массы выражается убывающей функцией, градиент которой - отрицательная величина.

Пример 5.

Определить количество теплоты, теряемое через бетонные стены здания площадью м² за время мин, если в помещении температура стены С, а снаружи С. Толщина стен  см.

Решение. Количество теплоты, передаваемое за счет теплопроводности стен, выражается законом Фурье:

                                       ,                               (1)

где – теплопроводность материала стены;  – градиент температуры, т. е. изменение температуры, приходящееся на 1 м толщины стены; S – площадь поверхности стены; t – время передачи теплоты.

Подставим числовые значения величин в формулу (1) и вычислим:

 

Раздел «Оптика. Атомная физика»

1.
Закон преломления                            
Формула тонкой линзы                              
Оптическая сила тонкой линзы         
Увеличение оптического прибора    
Световой поток                                  
Сила света                                          
Освещенность поверхности               
Светимость                                                  
Яркость                                              

Интерференция света

Оптическая длина пути луча                      
Оптическая разность хода лучей      
Расстояние между интерференционными полосами на экране
Оптическая разность хода световых лучей, отраженных от тонкой пластинки

 

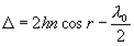
Дифракция света
Дифракция лучей, падающих на дифракционную решетку  ,

Разрешающая сила спектрального прибора

Разрешающая сила дифракционной решетки

Разрешающая сила объектива          

Тепловое излучение
Энергетическая светимость тела       
Закон Стефана Больцмана                
Закон смещения Вина                        
Формула Планка                                         

Энергия фотона                                 
Масса и импульс фотона                    ;
Уравнение Эйнштейна для фотоэффекта   
Комптоновская длина волны