2)если первая отбрасываемая цифра меньше 5, то последняя оставленная цифра не меняется, а если первая отбрасываемая цифра равна или больше 5, то последняя оставленная цифра увеличивается на 1.
Рассмотрим примеры.
Округлить число 23,97, содержащее четыре значащие цифры, 1) до трех;2) до двух;3) до одной значащей цифры.
Получим: 1) 24,0; 2) 24; 3) 20.
Округлить число 0,02397, содержащее четыре значащие цифры, 1) до трех; 2) до двух; 3) до одной значащей цифры.
Получим: 1) 0,0240; 2) 0,024; 3) 0,02.
ОЦЕНКА НЕОПРЕДЕЛЕННОСТИ РЕЗУЛЬТАТА РАСЧЕТА
Все расчеты мы производим с числами, имеющими неопределенности. В ходе любого расчета неопределенность всегда возрастает. Никакой расчет не в состоянии уменьшить неопределенность исходных данных. Покажем это на простом примере. Пусть нужно сложить два числа a и b, абсолютные неопределенности которых соответственно равны Δ a и Δ b. Имеем
.
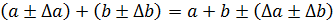Мы получили некоторое число
с абсолютной неопределенностью
.
При сложении или вычитании двух чисел, как мы видим, складываются их абсолютные неопределенности. Но при расчетах по физическим формулам мы имеем дело, как правило, с умножением и делением. Покажем, что при умножении или делении двух чисел или двух степеней складываются их относительные неопределенности.
Пусть расчетная формула выглядит следующим образом:
,
где m и n – целые числа, положительные или отрицательные. Если какое-то из этих чисел отрицательно, то соответствующая степень с противоположным показателем является делителем. Относительные неопределенности величин x, y, и z будут соответственно равны:
Прологарифмируем исходную формулу:
Найдем дифференциал левой и правой частей:
Три дифференциала примем за соответствующие абсолютные неопределенности: 
, 
, 
. Получим соотношение между относительными неопределенностями:
(1)
то есть относительные неопределенности множителей и делителей складываются, что и требовалось доказать. Притом складываются столько раз, сколько раз каждый из них входит в формулу множителем (делителем): m раз x и n раз y.
Полученная формула связи относительных неопределенностей справедлива только в том случае, если величины x и y или обе завышены или обе занижены. Но на практике неопределенности величин, входящих в формулу, как правило, компенсируют друг друга, и относительная неопределенность результата расчета оказывается меньше той, что дает формула (1). Поэтому неопределенность результата произведения принято вычислять как среднюю квадратичную из относительных неопределенностей множителей или делителей:
(2)
Как видно из формулы (2), неопределенность результата вычисления по формуле всегда будет больше неопределенности самого неточного числа из исходных данных.
Предлагаем Вам доказать, что 
при 
и 
.
Итак, в результате любых вычислений (расчетов) неопределенность всегда возрастает. Если исходные данные, использованные для расчетов, содержали не более двух значащих цифр, то результат расчета будет содержать только одну верную цифру – первую, вторая цифра уже будет содержать ошибку.
Поэтому при решении расчетных задач ответ не может содержать больше значащих цифр, чем их содержится в исходных данных. Остальные цифры должны быть отброшены с выполнением правила округления.
Рассмотрим еще один наглядный пример. Пусть нужно перемножить два числа: 24,2 и 3. В первом числе три значащие цифры, причем последняя в разряде десятых. Во втором числе только одна значащая цифра, а число десятых во втором числе не известно. Каждую неизвестную цифру будем обозначать рисунком.
Перемножим эти два числа столбиком. При этом результат умножения известной цифры на неизвестную и результат сложения известной цифры с неизвестной будем считать неизвестной цифрой и также обозначать рисунком.
| 2 4, 2 3, 7 2 6 7, |
Мы видим, что результат умножения содержит только одну известную, то есть верную, цифру.
Делаем вывод: если среди чисел, которые мы подставляем в расчетную формулу, есть хоть одно число, состоящее из одной цифры, то результат вычисления должен содержать только одну цифру, все остальные мы обязаны отбросить, используя правила округления.
Еще один пример. Нужно вычислить среднюю скорость движения по данным о пройденном пути 
и о затраченном времени 
. Каждое из заданных чисел содержит по 3 значащие цифры, из которых первые две являются верными. Сколько же значащих цифр должен содержать результат вычисления? Ответ – не меньше двух цифр!
Если исходные данные позволяют вычислить не только, сколько целых метров в секунду проходит тело, но и сколько дециметров и сколько сантиметров в секунду проходит тело, мы обязаны записать эти цифры, пусть даже это будут нули.
Обращаю внимание студентов на то, что ответ в расчетной задаче должен быть записан с необходимой и обоснованной точностью. Оцениваться будет не только правильность решения задачи, но и точность записанного результата вычисления.
При записи ответа помните, что нельзя без основания добавлять каждую следующую цифру, но также нельзя без основания отбрасывать следующую цифру, в том числе и 0.
Имейте в виду, что, например, 80 % – это 0,80, а не 0,8!
80 % = (80 
1) %, т.е. от 79 % до 81 %.
0,80 = (0,80 0,01), т.е. от 0,79 до 0,81,
а 0,8 = (08 0,1), т.е. от 0,7 до 0,9.
Отбрасывая 0 в конце, Вы огрубляете число в 10 раз!
Желаю всем успеха при написании контрольных работ.
СОДЕРЖАНИЕ
| Стр. | ||
| 1. 2 | Введение. Числа и цифры | 2 5 |
| 3. | Точность числа. | 7 |
| 4. | Оценка неопределенности результата расчета. | 14 |
