Иногда полезно иметь сигнал и его инверсию, т. е. два однородных сигнала, сдвинутые друг относительно друга по фазе на 180°. Получить такие сигналы нетрудно – нужно воспользоваться усилителем с общим эмиттером, коэффициент усиления которого равен – 1 (рис. 2.28).

Рис. 2.28. Схема расщепления фазы с единичным коэффициентом усиления.
Напряжение покоя на коллекторе устанавливают равным 0,75 UKK вместо привычного значения 0,5 UKK. Это делается с уже известной нам целью – получить симметричный выходной сигнал без срезов на любом из выходов. Напряжение на коллекторе может изменяться от 0,5 UKK до UKK, а на эмиттере – от потенциала земли до 0,5 UKK. Обращаем ваше внимание на то, что для симметричного усиления выходы схемы следует нагружать одинаковыми (или очень большими) импедансами.
Фазовращатель. На рис. 2.29 показан хороший пример использования схемы расщепления фазы выходного сигнала.

Рис. 2.29. Схема расщепления фазы с постоянной амплитудой.
Схема позволяет регулировать фазу выходного синусоидального сигнала (от нуля до 180°) при условии, что входной сигнал тоже представляет собой синусоиду; амплитуда сигнала при регулировке фазы сохраняется постоянной. Работу схемы помогает понять векторная диаграмма напряжений (см. гл. 1), для нашей схемы представленная на рис. 2.30; входной сигнал на ней изображен в виде единичного вектора, направленного вдоль действительной оси. Направления векторов, соответствующих сигналам UR и UK, должны быть такими, чтобы этим двум векторам соответствовал вектор постоянной длины, направленный вдоль действительной оси.

Рис. 2.30. Векторная диаграмма для схемы расщепления фазы.
В геометрии есть теорема, согласно которой геометрическим местом таких точек служит окружность. Итак, результирующий вектор (выходное напряжение) всегда имеет единичную длину, т. е. такую же, как вектор входного сигнала, так как R может изменяться от нуля до значений, значительно превышающих Ζ К на рабочей частоте. Обратите внимание, что величина фазового сдвига при данном положении потенциометра R зависит также от частоты входного сигнала.
Следует отметить, что в качестве схемы, обеспечивающей регулируемый сдвиг фаз, можно использовать простейший RC‑фильтр высоких (или низких) частот. Правда, в этом случае при регулировке фазы амплитуда выходного сигнала изменяется в широком диапазоне.
Отметим также, что фазовращатель RС‑типа нагружает схему расщепления фазы. В идеальном случае нагрузка представляет собой импеданс, который велик по сравнению с коллекторным и эмиттерным резисторами. Поэтому данная схема не может применяться в случаях, когда требуется обеспечить широкий диапазон фазовых сдвигов. В следующей главе приведена улучшенная схема фазовращателя.
Крутизна
В предыдущем разделе мы проанализировали работу усилителя с общим эмиттером следующим образом: а) предположив, что сигнал (напряжение) на базе изменяется в некоторых пределах, обнаружили, что напряжение на эмиттере имеет такой же размах; б) подсчитали эмиттерный ток; затем, пренебрегая незначительным влиянием тока базы, определили размах коллекторного тока и в) коллекторного напряжения. При этом коэффициент усиления есть просто отношение коллекторного напряжения (выходного) к напряжению на базе (входному).
Рассмотрим работу усилителя этого типа с другой точки зрения. Мысленно расчленим схему, как показано на рис. 2.31.

Рис. 2.31. Усилитель с общим эмиттером в качестве каскада с передаточной проводимостью, управляющий нагрузкой (резистивной).
Одна часть представляет собой управляемый напряжением источник тока, его ток покоя равен 1,0 мА, а коэффициент передачи составляет – 1 мА/В. Коэффициент передачи представляет собой отношение выходного сигнала к входному; в данном случае он измеряется в единицах [ток/напряжение] или [1/сопротивление]. Величина, обратная сопротивлению, называется проводимостью (величина, обратная реактивному сопротивлению, называется реактивной проводимостью; величина, обратная импедансу или полному сопротивлению, называется полной проводимостью), и единицей ее измерения служит сименс, раньше эту единицу измерения называли мо (обратный ом). Если коэффициент передачи измеряется в единицах проводимости, то такой усилитель называется усилителем с передаточной проводимостью; отношение Iвых / U вх называется крутизной и обозначается gm.
Итак, одна часть схемы представляет собой усилитель с передаточной проводимостью, коэффициент передачи которого (крутизна) составляет 1 мА/В (1000 мкСм или 1 мСм, а это есть не что иное, как 1/ RЭ). Другая часть схемы представляет собой нагрузочный резистор («усилитель»), преобразующий ток в напряжение. Резистор можно назвать усилителем с передаточным сопротивлением, его коэффициент усиления измеряется в единицах [напряжение/ток], т. е. в единицах сопротивления. В данном случае напряжение покоя (рабочее напряжение) – это UKK, а коэффициент передачи (передаточное сопротивление) равен 10 кВ/А (10 кОм), а это есть не что иное, как Rк.
Соединив эти две части последовательно, получим усилитель напряжения, общее усиление которого определяется произведением коэффициентов передачи составных частей. В данном случае: К = gmRк = Rк / RЭ = –10 – безразмерная величина, равная отношению [(выходное напряжение)/(входное напряжение)].
Описанный метод очень полезен для анализа усилителей, так как позволяет рассматривать составные части схемы независимо друг от друга. Например, для усилителя с передаточной проводимостью можно оценить величину gm для схем различной конфигурации и для иных элементов, например для полевых транзисторов. Затем можно рассмотреть нагрузку (или часть схемы с передаточным сопротивлением) и оценить, как связан коэффициент усиления с диапазоном изменения напряжения. Если вас интересует общее усиление по напряжению, то его можно определить следующим образом: КU = gmrm, где r m ‑ передаточное сопротивление нагрузки. В конечном счете замена простой активной нагрузки схемой с высоким передаточным сопротивлением позволяет получать для одного каскада усилителя величину коэффициента усиления, равную 10000 и выше. С помощью описанного метода удобно рассматривать каскодный усилитель, с которым вы познакомитесь ниже.
В гл. 4, где рассматриваются операционные усилители, приведено немало примеров усилителей, на входах и выходах которых действуют напряжения и токи, усилители напряжения, усилители тока, усилители с передаточной проводимостью, усилители с передаточным сопротивлением.
Предельный коэффициент усиления: границы применимости простейшей модели транзистора. В соответствии с нашей моделью коэффициент усиления по напряжению усилителя с общим эмиттером равен – RK / RЭ. Что произойдет, если сопротивление RЭ будет уменьшаться, стремясь к нулю? Согласно уравнению, коэффициент усиления будет при этом беспредельно возрастать. Однако измерения, выполненные в рассмотренной выше схеме, покажут, что, хотя при постоянном токе покоя, равном 1 мА, коэффициент усиления и растет, при RЭ = 0 (эмиттер заземлен) он становится равным всего 400.
Окажется также, что усилитель начнет при этом работать как нелинейный элемент (выходной сигнал не воспроизводит по форме в точности входной), входное сопротивление становится небольшим и нелинейным, а смещение начинает зависеть от температуры. Очевидно, что модель транзистора, которой мы пользовались, несовершенна и ее необходимо дополнить, чтобы она пришла в соответствие с измерениями, описанными выше, и некоторыми другими фактами, на которых мы еще остановимся. Модель, которую мы сейчас рассмотрим, будет достаточно точна и удовлетворит нас в дальнейшем.
Модель Эберса‑Молла для основных транзисторных схем
2.10. Улучшенная модель транзистора: усилитель с передаточной проводимостью (крутизной)
Существенную поправку следует внести в правило 4 (разд. 2.01), которое определяет, что IR = h21ЭIБ. Мы рассматривали транзистор как усилитель тока, вход которого работает как диод. Это приближение является грубым, но для некоторых практических случаев большей точности и не требуется. Однако для того чтобы понять, как работают дифференциальные усилители, логарифмические преобразователи, схемы температурной компенсации и некоторые другие практически полезные схемы, следует рассматривать транзистор как элемент с передаточной проводимостью ‑ коллекторный ток в нем определяется напряжением между базой и эмиттером.
Итак, правило 4 в измененном виде:
4. Если правила 1–3 соблюдены (разд. 2.01), то ток IК связан с напряжением UБЭ следующей зависимостью:
IК = Iнас [exp(UБЭ / UT) – 1]
где UT = kT / q = 25,3 мВ при комнатной температуре (20 °C), q – заряд электрона (1,60·10‑19 Кл), k – постоянная Больцмана (1,38·10‑23 Дж/К), Т – абсолютная температура в Кельвинах (К = °С + 273,16), Iнас ‑ ток насыщения транзистора (зависит от T). Тогда ток базы, который также зависит от UБЭ, можно приблизительно определить так:
IБ = IКh21Э
где «постоянная» h21Э обычно принимает значения от 20 до 1000 и зависит от транзистора, IК, UKЭ и температуры. Ток Iнас представляет собой обратный ток эмиттерного перехода. В активной области IК >> Iнас и членом – 1 можно пренебречь.
Уравнение для IК известно под названием «уравнение Эберса‑Молла». Оно приблизительно описывает также зависимость тока от напряжения для диода, если UT умножается на корректировочный коэффициент m со значением между 1 и 2.
Следует запомнить, что в транзисторе коллекторный ток зависит от напряжения между базой и эмиттером, а не от тока базы (ток базы в грубом приближении определяется коэффициентом h21Э). Экспоненциальная зависимость между током IК и напряжением UБЭ точно соблюдается в большом диапазоне токов, обычно от наноампер до миллиампер. На рис. 2.32 приведен график этой зависимости.

Рис. 2.32. Зависимость базового и коллекторного токов транзистора от напряжения между базой и эмиттером.
Если измерить ток базы при различных значениях коллекторного тока, то получим график зависимости h21Э от IК (рис. 2.33).
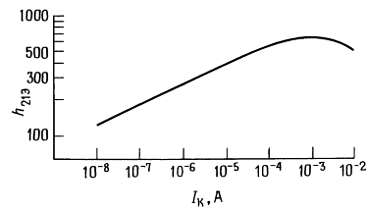
Рис. 2.33. Типичная зависимость коэффициента усиления по току для транзистора (h21Э) от коллекторного тока.
Согласно уравнению Эберса‑Молла, напряжение между базой и эмиттером «управляет» коллекторным током, однако это свойство нельзя использовать непосредственно на практике (создавать смещение в транзисторе с помощью напряжения, подаваемого на базу), так как велик температурный коэффициент напряжения между базой и эмиттером. В дальнейшем вы увидите, как уравнение Эберса‑Молла помогает решить эту проблему.
Практические правила для разработки транзисторных схем. На основании уравнения Эберса‑Молла получены некоторые зависимости, которые часто используют при разработке схем:
1. Ступенчатая характеристика диода. На сколько нужно увеличить напряжение UБЭ, чтобы ток IК увеличился в 10 раз? Из уравнения Эберса‑Молла следует, что UБЭ нужно увеличить на UT log e 10, или на 60 мВ при комнатной температуре. Напряжение на базе увеличивается на 60 мВ при увеличении коллекторного тока в 10 раз. Эквивалентным является следующее выражение I К = IK0eΔU/25, где ΔU измеряется в милливольтах.
2. Импеданс для малого сигнала со стороны эмиттера при фиксированном напряжении на базе. Возьмем производную от UБЭ по IК: rЭ UT / IK = 25/ IK Ом, где ток IK измеряется в миллиамперах. Величина 25/ IK Ом соответствует комнатной температуре. Это собственное сопротивление эмиттера rЭ выступает в качестве последовательного для эмиттерной цепи во всех транзисторных схемах. Оно ограничивает усиление усилителя с заземленным эмиттером, приводит к тому, что коэффициент усиления эмиттерного повторителя имеет значение чуть меньше единицы и не позволяет выходному сопротивлению эмиттерного повторителя стать равным нулю.
Этот параметр относится к параметрам малого сигнала. Отметим, что крутизна для усилителя с заземленным эмиттером определяется следующим образом: gm = 1/ rЭ.
3. Температурная зависимость. Глядя на уравнение Эберса‑Молла, можно предположить, что UБЭ имеет положительный температурный коэффициент. Однако, в связи с тем что ток Iнас зависит от температуры, напряжение UБЭ уменьшается на 2,1 мВ/°С. В грубом приближении оно пропорционально 1/ Табс, где Табс ‑ абсолютная температура.
И еще одна зависимость пригодится нам на практике, правда, она не связана с уравнением Эберса‑Молла. Речь идет об эффекте Эрли, описанном в разд. 2.06, который накладывает ограничения на выходную характеристику транзистора как источника тока.
4. Эффект Эрли. UБЭ хоть и в слабой мере, но зависит от UKЭ при постоянном токе IК. Этот эффект обусловлен изменением эффективной ширины базы и описывается следующей приблизительной зависимостью: ΔUБЭ = –α UКЭ, где α ~= 0,0001.
Мы перечислили основные соотношения, которые могут быть полезны на практике. Эти соотношения, а не сами уравнения Эберса‑Молла, используются при разработке транзисторных схем.






