Прямые, параллельные плоскостям проекций

Угол пространства

Координата I II III IV

X + + + +

Y + - - +

Z + + - -

Билет №7 с23

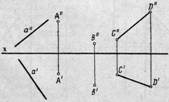
На эпюре прямая может быть задана: проекциями прямой (а' и а"); проекциями двух точек, принадлежащих прямой (А', А" и В', В"); проекциями отрезка прямой (С'D' и C" D").

Билет№8 с 23

Особый интерес представляют прямые частного положения, т. е. прямые, расположенные определенным образом относительно плоскостей проекций: параллельные, перпендикулярные и принадлежащие плоскостям проекций.

Прямые, параллельные плоскостям проекций

1. Горизонтальная прямая h.

Горизонтальная прямая — это прямая, параллельная горизонтальной плоскости проекций π₁. Так как все точки этой прямой равноудалены от плоскости проекций π₁ (координаты z всех точек прямой одинаковы), то фронтальная и профильная проекции прямой соответственно параллельны координатным осям х и у.

2. Фронтальная прямая f.

Фронтальная прямая — это прямая, параллельная фронтальной плоскости проекций π₂, Так как все точки этой прямой равноудалены от плоскости проекций π₂(координаты у всех точек прямой одинаковы), то горизонтальная и профильная проекции прямой соответственно параллельны координатным осям х и z.

3. Профильная прямая р.

Профильная прямая — это прямая, параллельная профильной плоскости проекций я₃. Так как все точки этой прямой равноудалены от плоскости проекций π₃ (координаты х всех точек прямой одинаковы), то горизонтальная и фронтальная проекции прямой соответственно параллельны координатным осям у и z.

Прямые, принадлежащие ПП.

Прямые, принадлежащие плоскостям проекций, являются частным случаем горизонтальных, фронтальных и профильных прямых.

Билет №9 с26

Из инвариантного свойства 3 следует, что проекции точки К (К', К" и К'"), принадлежащей прямой а, должны принадлежать соответствующим проекциям этой прямой, т. е.

Если хотя бы одна проекция точки не принадлежит соответствующей проекции прямой, то эта точка не принадлежит прямой.

Из инвариантного свойства 4 следует, что проекции точки К (К', К" и К'"), принадлежащей отрезку прямой АВ, делят соответствующие проекции отрезка в том же отношении, в каком точка К делит отрезок АВ, т. е.

Билет №10 с 27

Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны. Рассмотрим изображение этих прямых на эпюре.

1. Пересекающиеся прямые. Пересекающимися прямыми называются прямые, имеющие одну общую точку.

Из инвариантного свойства 5 следует, что проекция точки пересечения прямых а и b есть точка пересечения проекций этих прямых.

2. Параллельные прямые. Параллельными прямыми называются прямые, пересекающиеся в несобственной точке (т. е. прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).

Из инвариантного свойства 6 следует, что проекции параллельных прямых а и b параллельны.

3. Скрещивающиеся прямые. Скрещивающиеся прямые — это прямые, не лежащие в одной плоскости, это прямые, не имеющие общей точки. На эпюре точки пересечения проекций этих прямых не лежат на одном перпендикуляре к оси х (в отличие от пересекающихся прямых).

4. Перпендикулярные прямые. Особый интерес с точки зрения решения задач начертательной геометрии представляют прямые перпендикулярные. Из инвариантного свойства 9.2 следует, что любой угол (в том числе и прямой) между двумя пересекающимися прямыми проецируется без искажения, если обе стороны этого угла параллельны плоскости проекций. Прямой угол по инвариантному свойству 10 проецируется в натуральную величину, если хотя бы одна его сторона параллельна плоскости проекций.

На эпюре пересекающиеся прямые изображаются пересекающимися линиями на обоих видах, скрещивающиеся прямые –пересекающимися линиями на одном виде и непересекающимися

Билет №11 с 29

Следом прямой линии называется точка пересечения прямой с плоскостью проекций. В системе двух плоскостей проекций Л! и л₂ прямая в общем случае имеет два следа: горизонтальный Н (Н', Н") и фронтальный F (F ', F ") — точки пересечения прямой соответственно с горизонтальной и фронтальной плоскостями проекций.

Горизонтальный след прямой — это такая точка этой прямой, координата z которой равна нулю (z = 0). Фронтальный след прямой — это точка прямой, координата у которой равна нулю (у = 0). Пользуясь этим правилом, нетрудно определить следы прямой на эпюре.

В начертательной геометрии считается, что наблюдатель расположен в первом пространственном углу на бесконечном расстоянии от плоскостей проекций, поэтому видимыми геометрическими фигурами будут только те, которые расположены в первом углу. Проекции этих фигур в ортогональных и аксонометрических проекциях показываются сплошными линиями. Фигуры, расположенные в других пространственных углах, не видны наблюдателю, и их проекции показываются штриховыми линиями.

Билет №12 c 30

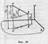
На рис. 43 показаны в аксонометрической проекции отрезок АВ и его горизонтальная проекция А'В'. Проведя прямую ВВ₁ параллельную горизонтальной проекции отрезка А'В' (ВВ₁ II А'В'), получим прямоугольный треугольник АВВ₁.

Длина отрезка АВ равна гипотенузе этого треугольника, катетами которого являются горизонтальная проекция отрезка А'В' и разность координат z точек А и В (Δz = = z _А – z_B).

Как известно, угол наклона прямой к плоскости равен углу между этой прямой АВ и ее проекцией на плоскость (А'В¹).

Следовательно, угол треугольника АВВ₁ лежащий против катета Δz, равен углу наклона отрезка АВ к горизонтальной плоскости проекций π₁ (угол α°).

Аналогично рассуждая (рис. 44), можно показать, что длина отрезка АВ равна гипотенузе треугольника, катетами которого являются фронтальная проекция отрезка А"В" и разность координат у точек А и В

(ΔУ = У а - У в)-

Угол этого треугольника, лежащий против катета Δу, равен углу наклона отрезка АВ к фронтальной плоскости проекций π₂(угол β°).

По аналогии длина отрезка АВ может быть определена и как гипотенуза треугольника, катеты которого — профильная проекция отрезка А'"В'" и разность координат х (Δх = х _A – х _B) точек А и В. Угол γ° этого треугольника, лежащий против катета Δx, определяет угол наклона отрезка АВ к профильной плоскости проекций π₃.

На рис. 45 показан пример определения длины отрезка АВ и углов наклона его к плоскостям проекций (L _АВ — длина отрезка АВ; α°, β°, γ° — углы наклона его соответственно к плоскостям проекций π₁, π₂, π₃).

Билет №13 с 32

Метод конкурирующих точек используется в начертательной геометрии для определения взаимной видимости двух геометрических фигур.

Конкурирующими точками называются такие точки пространства, у которых совпадают какие-либо две одноименные проекции. Так, на рис. 46 показаны конкурирующие точки А к В (совпадают горизонтальные проекции А' = В') и С, D (совпадают фронтальные проекции С" ≡ D ").

Метод конкурирующих точек заключается в определении взаимной видимости точек по их несовпадающим проекциям. Так, точка В находится выше точки А относительно плоскости π₁ (z _в > z _А), поэтому на плоскости π₁ видна точка В, которая закрывает точку А (считается, что наблюдатель смотрит на плоскости проекций из бесконечности и направление луча зрения параллельно проецирующему лучу s).

На плоскости π₂ видна точка О, так как она находится ближе к наблюдателю (дальше от плоскости π₂, У _D > Ус) и закрывает невидимую точку С.

Пользуясь этим методом (рис. 47), можно определить, что прямая а проходит над прямой b, так как точка А, принадлежащая этой прямой а, расположена выше точки В, находящейся на прямой b (z _л > z _в).

В дальнейшем методом конкурирующих точек будем пользоваться при определении видимости пересекающихся геометрических фигур.

Билет №14 с 34

На эпюре плоскость может быть задана графически одним из следующих способов:

1) тремя точками, не лежащими на одной прямой;

2) прямой и точкой вне ее;

3) двумя пересекающимися прямыми;

4) двумя параллельными прямыми;

5) плоской фигурой (напр. треугольник или параллелограмм );

6) следами. Следом плоскости αназывается линия пересечения этой плоскости с плоскостью проекций. В системе двух плоскостей проекций π₁ и π₂ плоскость в общем случае имеет два следа: горизонтальный h_0α (h’_0α, h”_0α) и фронтальный f_0α (f’_0α, f”_0α), которые являются пересечением плоскости α соответственно с горизонтальной и фронтальной плоскостями проекций.

Билет №15 с 36.

Плоскости, перпендикулярные плоскостям проекций (проецирующие плоскости)

1. Горизонтально проецирующая плоскость α перпендикулярная π₁. Плоскость а, перпендикулярная горизонтальной плоскости проекций π₁, называется горизонтально проецирующей (рис. 53, 54).

Основным свойством горизонтально проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π₁ в прямую линию (горизонтальный след плоскости h_0α, Рис- 53, 54).

Угол β, который составляет горизонтальный след плоскости h_0α с координатной осью х, равен углу наклона плоскости α к плоскости проекций π₂. Фронтальный след такой плоскости перпендикулярен оси х ( f_0α перпендикулярен х).

На рис. 54 показаны примеры изображения на эпюре горизонтально проецирующих плоскостей α, β и γ (D Е F).

2. Фронтально проецирующая плоскость β перпендикулярна π₂. Плоскость β, перпендикулярная фронтальной плоскости проекций π₂, называется фронтально проецирующей

(рис. 55, 56).

Основным свойством фронтально проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π₂ в прямую линию (фронтальный след плоскости f₀_β рис. 55, 56). Угол α°, который составляет фронтальный след плоскости f₀_β с координатной

осью х, равен углу наклона плоскости β к плоскости проекций π₁. Горизонтальный след такой плоскости перпендикулярен

оси х (h₀_β перпендикулярен x).

На рис. 55 показаны примеры изображения на эпюре фронтально проецирующих плоскостей β,γ и δ.