Постановка задачи:
В общем случае не линейное уравнение может быть записано в виде 
(1)
– определена и непрерывна на конечном или бесконечном интервале [a;b].
Любое число ε принадлежащее [a;b], такое, что 
назовем корнем уравнения (1).
Не линейные уравнения с одной переменной подразделяются на алгебраические и трансцендентные.
Уравнение (1) является алгебраическим, если функция в результате алгебраических преобразований может быть представлена в виде:
, где 
Если левую часть уравнения невозможно представить в таком виде, то уравнение называется трансцендентное.
Решить уравнение (1) это значит установить имеет ли оно корни, установить сколько корней и определить эти корни с заданной точностью или доказать, что уравнение не имеет корней. Задача численного нахождения корня уравнения (1) состоит из 2-х этапов:
1) Отделение корней
2) Уточнение корней
Отделение корней – это нахождения достаточно малых отрезков в которых локализован один корень.
Уточнение – вычисление корней с заданной точностью.
Выбор численного метода зависит от числа корней, от задания точности и от поведения функции .
Метод половинного деления
Дано нелинейное уравнение:
Найти корень уравнения, принадлежащий интервалу [a;b], с заданной точностью ε.
Для уточнения корня методом половинного деления последовательно осуществляем следующие операции:
Делим интервал пополам:
[a;b].
В качестве нового интервала изоляции принимаем ту половину интервала, на концах которого функция имеет разные знаки (рис.4.4).
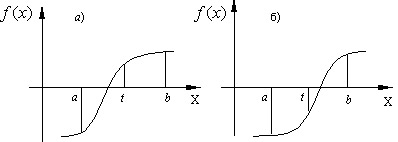
Для этого:
a) Вычисляем значение функции f(x) в точках a и t.
b) Проверяем: если f(a)f(t) < 0, то корень находится в левой половине интервала [a,b] (рис.4.4.а). Тогда отбрасываем правую половину интервала и делаем переприсвоение b=t.
c) Если f(a)f(t) < 0 не выполняется, то корень находится в правой половине интервала [a,b] (рис.4.4.б). Тогда отбрасываем левую половину и делаем переприсвоение a=t. В обоих случаях мы получим новый интервал [a,b] в 2 раза меньший предыдущего.
Процесс, начиная с пункта 1, циклически повторяем до тех пор, пока длина интервала [a,b] не станет равной либо меньшей заданной точности, т.е. 
≤ε.
Метод - половинного деления имеет много достоинств. Главным достоинством этого метода является то, что для приближенных решений автоматически получается оценка точности. Второе достоинство данного метода состоит в том, что этот метод легко реализуем. Однако у этого метода есть и недостатки. Для реализации этого метода мы должны знать отрезок, на концах которого функция принимает значения разного знака. А также этот метод является сугубо скалярным и не может быть обобщен на многомерный случай.
