Расчетная схема второстепенной балки – многопролетная неразрезная конструкция. Опорами служат в крайних пролетах – кирпичная стена и главная балка, в средних пролетах – главные балки.
Расчетные средние пролеты исчисляются как расстояния в свету между гранями главных балок, а за расчетные крайние пролеты принимаются расстояния между гранями главных балок и серединами площадок опирания на стены (рис. 6).
При ширине ребер главных балок (ориентировочно) 250 мм и глубине заделки второстепенных балок и стены на 250 мм:
,
.
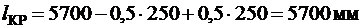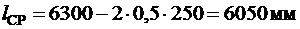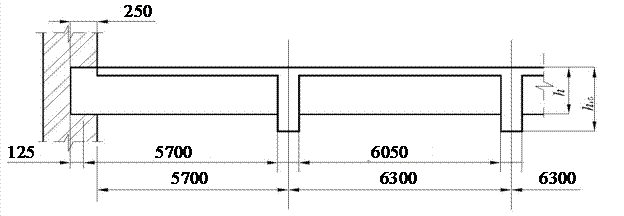
Рис. 6 Общий вид второстепенной балки
Статический расчет
Сбор нагрузок приведен в табл. 3.
Таблица 3
Расчетные нагрузки на наиболее нагруженную второстепенную балку Б-1 с грузовой площадью шириной 2,1 м, равной расстоянию между осями балок
· полная расчетная нагрузка
,
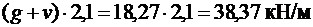· постоянная и временная длительная
,
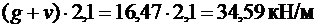Расчетные изгибающие моменты в неразрезных балках (рис. 7) с равными или отличающимися не более чем на 10 % пролетами (l ср : l кр= 605: 570 = 1,06 < 1,10) в соответствии с [6] с учетом перераспределения усилий, в следствие пластических деформаций определяются по формулам:
· в крайних пролетах
;
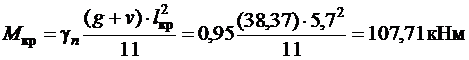· в средних пролетах и над средними опорами
;
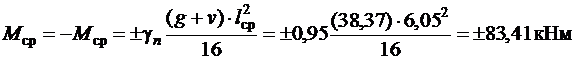· над вторыми от конца промежуточными опорами В
,
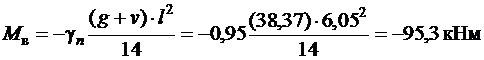где l – больший из примыкающих к опоре В расчетный пролет.
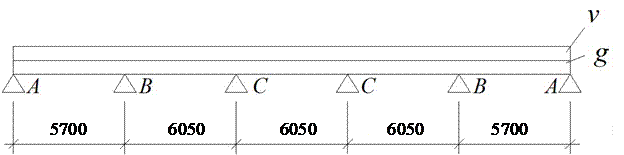
Рис. 7. Расчетная схема второстепенной балки
Величины значений возможных отрицательных моментов в средних пролетах при невыгоднейшем загружении второстепенной балки временной нагрузкой в соответствии с [6] определяются по огибающим эпюрам моментов для неразрезной балки в зависимости от соотношения временной и постоянной нагрузок по формуле
,
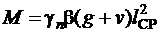где b – коэффициент, принимаемый по приложению 2.
При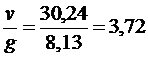 
для сечений на расстоянии 0,2 l от опоры В во втором пролете bII = - 0,0375 и 0,2 l от опоры С в третье пролете – bIII = - 0,0295.
;
.
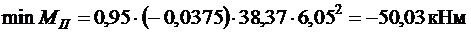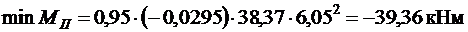Расчетные поперечные силы
;
;
;
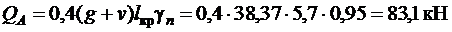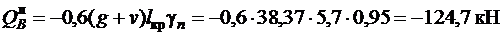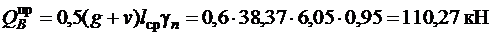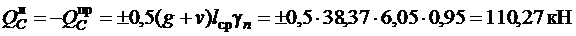
Определение размеров сечения второстепенной балки
Принимаем для балки бетон класса В 15. Поскольку отношение постоянных и длительных нагрузок к полным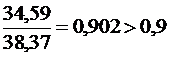 
, коэффициент 
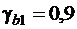и 
; 
;.
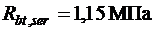
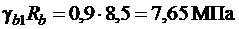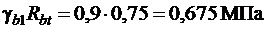В качестве рабочей в каркасах используем стержневую арматуру периодического профиля класса А 400 с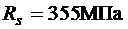 
и сварные сетки из обыкновенной арматурной проволоки класса В 500 с 
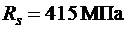. Поперечная и монтажная арматура – класса А 240 с 
, 
.
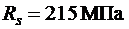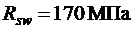Необходимую высоту балки определяем по максимальному опорному моменту, задавшись шириной ребра b = 250 мм и приняв относительную высоту сжатой зоны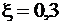 
, поскольку в соответствии с [6] расчетные усилия в балке подсчитаны с учетом перераспределения усилий и возможного образования в опорных сечениях пластических шарниров.
При ,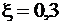 
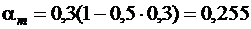, расчетная высота сечения
.
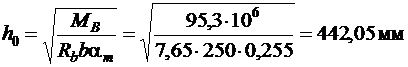Полная высота сечения при однорядном расположении стержней продольной арматуры
.
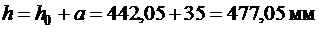Принимаем с округлением до размера, кратного 100 мм, при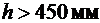 
мм высоту второстепенной балки h = 500 мм, ширину ребра 
.
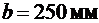Примечание. Проверка достаточности принятых размеров сечения производится согласно п. 3.30 [3] из условия обеспечения прочности балки по наклонной полосе между наклонными трещинами с учетом поперечного армирования.
Расчет продольной рабочей арматуры
В соответствии с эпюрами моментов плита, работающая совместно с балкой, в пролетах располагается в сжатой зоне, поэтому за расчетное принимается тавровое сечение с полкой в сжатой зоне.
В опорных сечениях плита расположена в растянутой зоне и при образовании в ней трещин из работы выключается. Поэтому вблизи опор за расчетное принимается прямоугольное сечение с шириной равной 250 мм.
При действии в средних пролетах отрицательных моментов плита в них также оказывается в растянутой зоне, поэтому за расчетное сечение балки также принимается прямоугольное сечение.
Расчетная ширина полки в элементе таврового сечения при
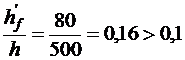в соответствии с п. 3.26 [3] принимается меньшей из двух величин:
,
.
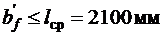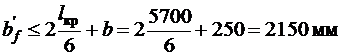Принимаем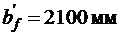 
.
Расчет продольной арматуры в пролетных и опорных сечениях второстепенной балки, выполненной для двух вариантов армирования, сведен в табл. 4. В опорных и пролетных сечениях предусмотрено армирование сварными сетками с рабочей арматурой класса А 400. Монтажная и поперечная арматура – класса А 240 (рис. 8).
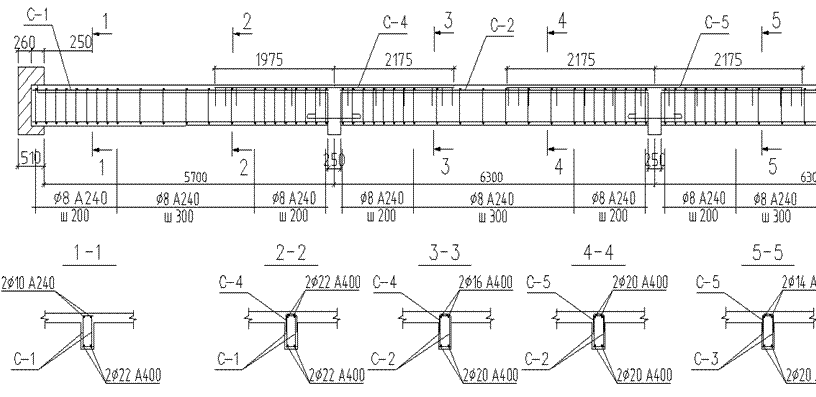
Рис. 8. Схема армирования второстепенной балки
Таблица 4
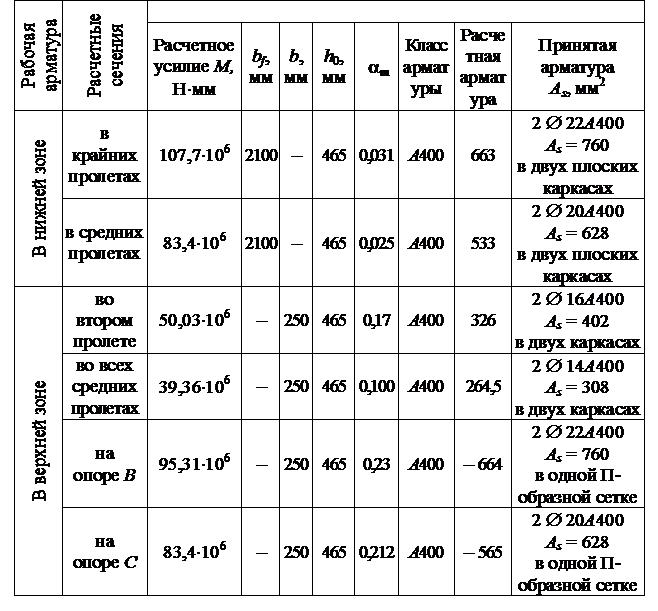
Расчет балки на действие поперечных сил у опоры А
Минимальная поперечная сила на опорах: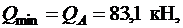 
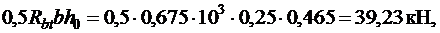
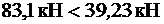, поперечная арматура в балке должна ставиться по расчету.
Принимаем поперечную арматуру класса A 240 с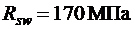 
(см. табл. 2.6 [3]). В двух плоских каркасах при диаметре стержней продольной арматуры 22 мм поперечные стержни из условия технологии сварки принимаем диаметром 6 мм (
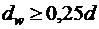, см. п. 9. ГОСТ 14098-91).
При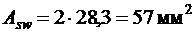 
(2Æ6 А 240), 
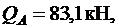максимально допустимый шаг поперечных стержней у опор в соответствии с п. 5.21 [3] при 
:
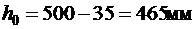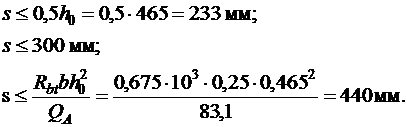
Принимаем шаг поперечных стержней в каркасах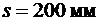 
.
Расчет прочности по полосе между наклонными сечениями.
Расчет прочности по наклонной полосе между наклонными сечениями производим из условия 3.43 [3]
,
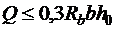где Q принимается на расстоянии не менее h 0 от опоры.
,
,
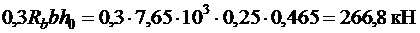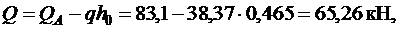
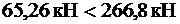прочность наклонной полосы на сжатие обеспечена.
Расчет прочности на действие поперечной силы по наклонному сечению
Усилие в хомутах на единицу длины элемента равно [3]
.
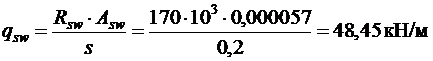Так как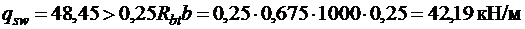 
,
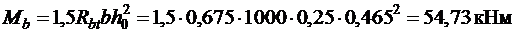[3].
Определяем длину проекции невыгоднейшего наклонного сечения c.
При расчете элемента на действие равномерно распределенной нагрузки q значение c принимают равным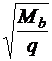 
, а если при этом 
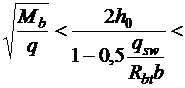или 
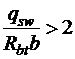, то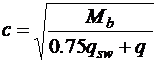 
(3.32 [3]).
,
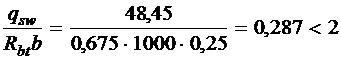так как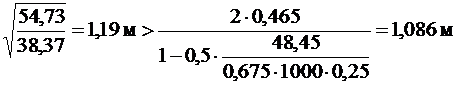 
,
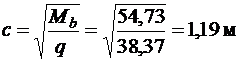, не более 
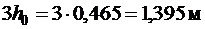(п. 3.32 [3]).
Принимаем длину проекции невыгоднейшего наклонного сечения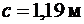 
.
Длину проекции наклонной трещины c 0 принимают равным c, но не более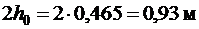 
(п. 3.31 [3]). Принимаем длину проекции наклонной трещины 
.
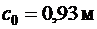Тогда поперечная сила воспринимаемая хомутами равна
.
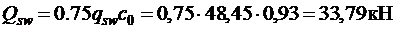Поперечная сила, воспринимаемая бетоном (п. 3.31 [3])
,
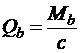но не более
,
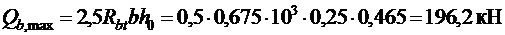и не менее
.
.
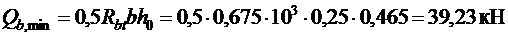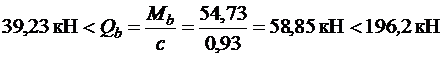Принимаем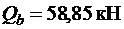 
.
Расчет изгибаемых элементов по наклонному сечению производят из условия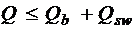 
, где Q – поперечная сила в наклонном сечении с длиной проекции c; при вертикальной нагрузке, приложенной к верхней грани элемента, значение Q принимается в нормальном сечении, проходящем на расстоянии c от опоры; при этом следует учитывать возможность отсутствия временной нагрузки на приопорном участке длиной c.
.
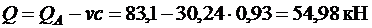При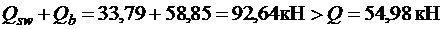 
, т. е. прочность наклонных сечений у опоры А обеспечена.
Проверка прочности наклонного сечения у опоры А на действие момента
Поскольку продольная растянутая арматура при опирании на стену не имеет анкеров, расчет наклонных сечений на действие момента необходим.
Принимаем начало наклонного сечения (рис. 9) у грани опоры. Отсюда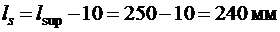 
.
Опорная реакция балки равна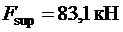 
, а площадь опирания балки 
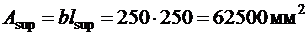, откуда
,
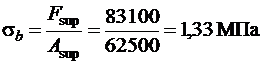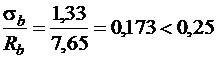, следовательно, 
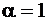. Из табл. 3.3 [3] при классе бетона В 15, классе арматуры А 400 и 
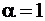находим 
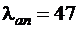. Тогда, длина анкеровки при d s = 22 ммравна 
.
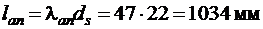Усилие в продольной арматуре в зоне анкеровки
.
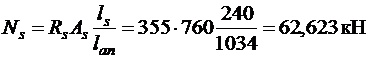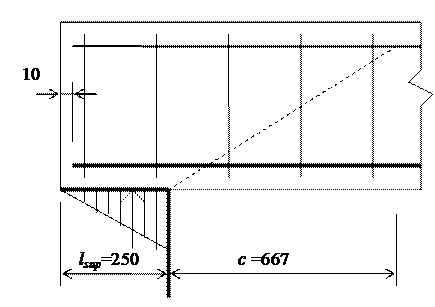
Рис. 9. Расчетная схема по наклонному сечению на действие изгибающего момента
Поскольку к растянутым стержням в пределах длины l s приварены 4 вертикальных и 1 горизонтальный поперечных стержня, увеличим усилие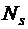 
на величину 
.
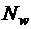Принимая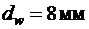 
, 
, 
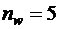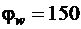(табл. 3.4[3]), получаем
.
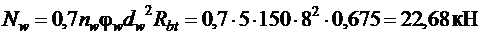Отсюда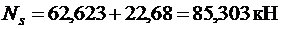 
.
Определяем максимально допустимое значение 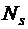. Из табл. 3.3 [3] при 
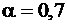находим 
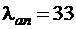, тогда
,
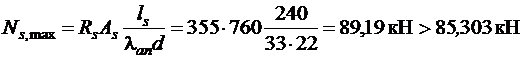т.е. оставляем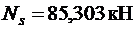 
.
Определим плечо внутренней пары сил
>
.
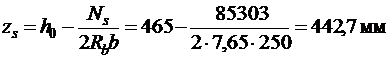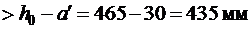Тогда момент, воспринимаемый продольной арматурой, равен
.
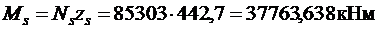По формуле 3.48 [3] вычислим величину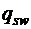 
.
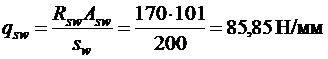Определим длину проекции невыгоднейшего наклонного сечения по формуле 3.76 [3], принимая значение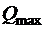 
равным опорной реакции балки
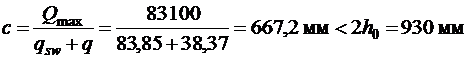
Момент, воспринимаемый поперечной арматурой, равен
.
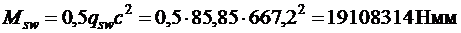Момент в наклонном сечении определяем как момент в нормальном сечении, расположенном в конце наклонного сечения, т е. на расстоянии от точки приложения опорной реакции, равной x = l sup/3 + + c = 250/3 + 667,2 = 750,5 мм
.
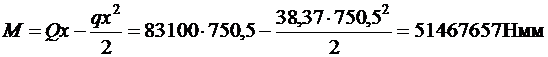Проверяем условие 3.69 [3]:
,
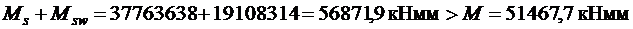т. е. прочность наклонных сечений по изгибающему моменту обеспечена.
Расчет балки на действие поперечных сил у опор B и C
У опор В и С при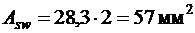 
(2Æ6 А 240). 
, 
.
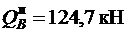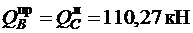Максимально допустимый шаг поперечных стержней у опор в соответствии с п. 5.21 [3] при h 0 = 500 – 35 мм = 465 мм:
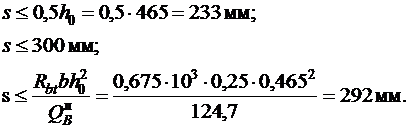
Принимаем шаг поперечных стержней в каркасах s = 200 мм.
Расчет прочности по полосе между наклонными сечениями
Расчет прочности по наклонной полосе между наклонными сечениями производим из условия 3.43 [3].
,
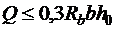где Q принимается на расстоянии не менее h 0 от опоры.
,
,
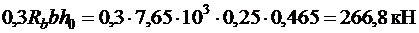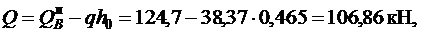
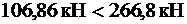прочность наклонной полосы на сжатие обеспечена.
Расчет прочности на действие поперечной силы по наклонному сечению
У опоры В 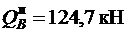. При прочих равных параметрах (см. расчет по наклонному сечению у опоры А) проверим достаточность принятой поперечной арматуры:
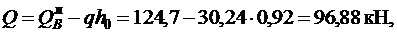
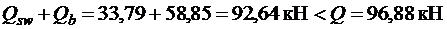, т.е. прочность наклонных сечений у опоры B недостаточна (см. п. 3.31 [3]).
Увеличиваем диаметр поперечных стержней до 8 мм и оставляем шаг 200 мм. Тогда при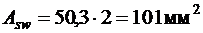 
(2Æ8 А 240) снова проверяем прочность по наклонному сечению.
.
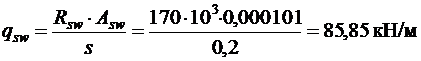Так как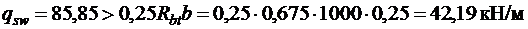 
,
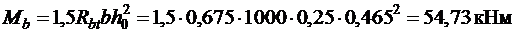[3].
.
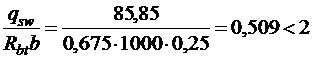Так как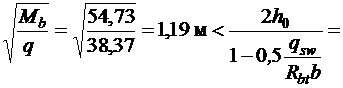 
,
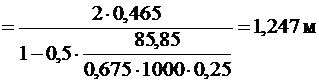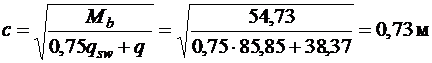, но не более 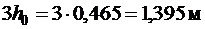(п. 3.32 [3]).
Принимаем длину проекции невыгоднейшего наклонного сечения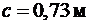 
.
Длину проекции наклонной трещины c 0 принимают равным c, но не более 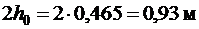(п. 3.31 [3]).
Принимаем длину проекции наклонной трещины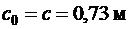 
. Тогда
.
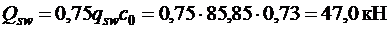Поперечную силу, воспринимаемую бетоном, определяют по формуле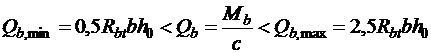 
.
,
,
.
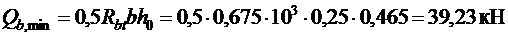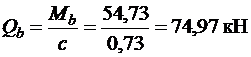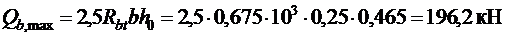Принимаем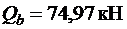 
.
Расчет изгибаемых элементов по наклонному сечению производят из условия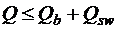 
, где Q – поперечная сила в наклонном сечении с длиной проекции c; при вертикальной нагрузке, приложенной к верхней грани элемента, значение Q принимается в нормальном сечении, проходящем на расстоянии c от опоры; при этом следует учитывать возможность отсутствия временной нагрузки на приопорном участке длиной c.
.
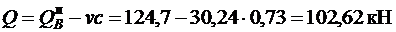При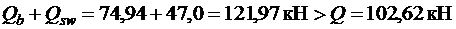 
, т.е. прочность наклонных сечений у опоры В обеспечена.
Согласно п.5.21 [3] шаг хомутов(s w)
· у опоры должен быть не более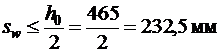 
и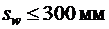 
;
· в пролете не более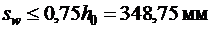 
и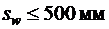 
.
Окончательно устанавливаем во всех пролетах на приопорных участках длиной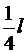 
поперечную арматуру диаметром 8 мм с шагом 200 мм, а на средних участках с шагом 300 мм.
У опоры В справа и у опоры С слева и справа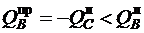 
и одинаковой поперечной арматуре прочность наклонных сечений также обеспечена.
Расчет ширины раскрытия наклонных трещин
В учебном пособии этот расчет для второстепенной балки не производится. Аналогичный расчет выполнен для продольного ребра сборной ребристой панели.
Определение ширины раскрытия нормальных трещин
Расчет производится в соответствии с п. 7.2.12 [2] на действие нормативных нагрузок. В учебном пособии этот расчет для второстепенной балки не производится. Аналогичный расчет выполнен для продольного ребра сборной ребристой панели.
