Три взаимно перпендикулярные оси в пространстве (координатные оси) с общим началом О и одинаковой масштабной единицей образуют декартову прямоугольную (кратко - прямоугольную) систему координат в пространстве. Оси упорядочены, т.е. указано, какая из осей считается первой (она называется осью абсцисс и обозначается Ох), какая - второй (ось ординат Оу) и какая - третьей (ось аппликат Oz).
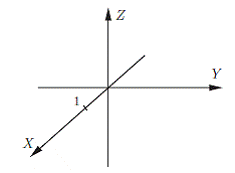
Вектором называется направленный отрезок, имеющий определенную длину, т.е. отрезок определенной длины, у которого одна из ограничивающих его точек принимается за начало, а вторая - за конец. Если А - начало вектора и В - его конец, то вектор обозначается символом 
. Вектор можно обозначать и одной малой латинской буквой с чертой над ней (например, 
). Изображается вектор отрезком со стрелкой на конце.
Длина вектора называется его модулем и обозначается символом 
. Модуль вектора обозначается 
. Вектор , для которого =1, называется единичным.
В пространстве помимо координат точки вводятся координаты вектора. 
.
Координаты суммы (разности) двух векторов равны суммам (разностям) соответствующих координат этих векторов 
Как найти координаты вектора? Как и на плоскости: из координаты конца
вычитаем координату начала.
|
Длина вектора AB в пространстве –– это расстояние между точками A и B.
Координаты точки М определяются формулами:
Если точка М является серединой отрезка, то ее координаты равны
полусуммам соответствующих координат концов отрезка.
Скалярным произведением двух векторов называется
произведение длин этих векторов на косинус угла между ними.
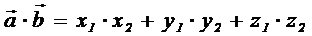Скалярное произведение двух векторов выражается формулой:
Угол между векторами можно найти, используя формулу скалярного произведения векторов:
Плоскость в пространстве задается уравнением Ax + By + Cz + D = 0.
Числа А, В, С – координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Занятие 1. Расстояние от точки до прямой
Расстояние от точки до прямой - это длина перпендикуляра, опущенного из точки на эту прямую.
В практических задачах мы сначала будем искать плоскость, которую определяют прямая и точка.
Затем, в определенной плоскости строить перпендикуляр из точки на заданную прямую.
А
Занятия 2 -3. Расстояние от точки до плоскости.
На первом занятии рассматриваются задачи, решаемые с помощью «метода построений». На втором - с помощью метода координат.
Решение данной задачи позволяет решать задачи о нахождении расстояния между параллельными плоскостями, между параллельными прямой и плоскостью, между скрещивающимися прямыми. Поэтому необходимо подробнее остановиться на отработке учащимися навыков решения задач о нахождении расстояния от точки до плоскости.
Занятия 4 -6. Угол между прямыми.
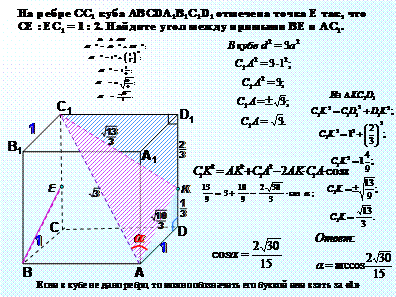
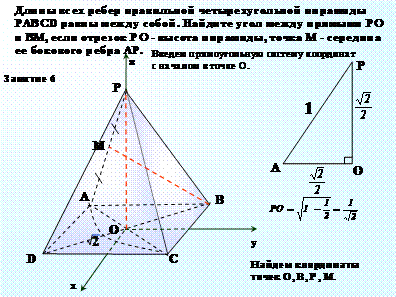
На четвертом занятии рассматриваются задачи, решаемые с помощью «метода построений». Модель – куб. На пятом и шестом - с помощью метода координат. Модели – призмы и пирамиды.
Занятия 7 -9. Угол между прямой и плоскостью.
На седьмом занятии рассматриваются задачи, решаемые с помощью «метода построений». Модель – куб. На восьмом и девятом - с помощью метода координат. Модели – призмы и пирамиды.
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов:
Пусть a - вектор, лежащий на прямой m (или параллельный ей), n - нормаль к
плоскости α..
Занятия 10 -12. Угол между двумя плоскостями.
На 10 занятии рассматриваются задачи, решаемые с помощью «метода построений». Модель – куб, четырехугольная призма. На 11 и 12 - с помощью метода координат. Модели – призмы и пирамиды.
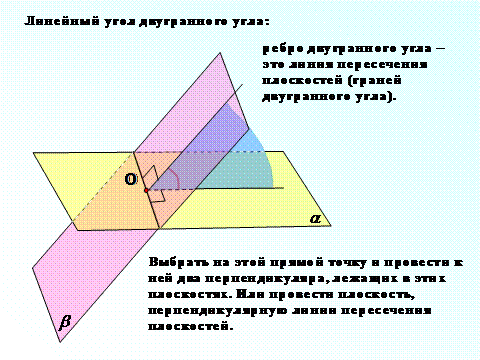
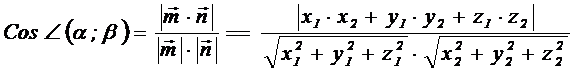Угол между плоскостями равен углу между нормалями к этим плоскостям:
Занятие 13. Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми равно длине отрезка их общего перпендикуляра.
Задачу данного вида можно свести к задаче о вычислении расстояния от точки до плоскости, поэтому можно применить формулу расстояния от точки до плоскости, применяя координатный метод.
Источники:
1. Атанасян Л.С.и др. Геометрия, 10-11: учеб. для общеобразоват. учреждений: базовый и профил. уровни.- 17 – е изд.- М.: Просвещение, 2008.
2. Беликова И. Задание С2: Решаем методом координат // Математика, 2010, № 20.
3. Смирнов В.А. ЕГЭ-2011. Математика. Задача С2. Геометрия. Стереометрия / под ред. А.Л. Семенова, И.В. Ященко. — М.: МЦНМО, 2011.
4. Шабунин М.И. Математика для поступающих в вузы: пособие. — 2-е изд., испр. и доп. — М.: БИНОМ, 2003.
5. http://ege-ok.ru/
6. http://nsportal.ru/
7. http://gym1.ucoz.ru/
8. http://kopilkaurokov.ru/
9. http://alexlarin.net/
10. http://reshuege.ru/
11. И.М. Смирнова, В.А. Смирнов. Геометрия. Расстояния и углы в пространстве. – М.: Экзамен, 2009 (Серия «ЕГЭ. сто баллов»).
12. И.М. Смирнова, В.А. Смирнов. Геометрия. Объемы и площади поверхностей пространственных фигур. – М.: Экзамен, 2009 (Серия «ЕГЭ. сто баллов»).
13. В.А. Смирнов. Геометрия. Стереометрия: Пособие для подготовки к ЕГЭ / Под редакцией И.В. Ященко и А.В. Семенова. – М.: МЦНМО, 2009.
