И вывод расчетной формулы
Основная идея метода Клемана – Дезорма заключается в следующем:
для экспериментального определения коэффициента Пуассона необходимо осуществить два газовых процесса - адиабатическое расширение и изохорическое нагревание газа в неизолированном сосуде.
Процессы, происходящие в этом эксперименте, можно изобразить на диаграмме (рисунок 8). Адиабатическое расширение газа (кривая 1-2) характеризуется понижением температуры от комнатной (Т0) до Т1 и понижением давления газа от Р1 до атмосферного (Р0).
При изохорическом нагревании газа в закрытом сосуде (кривая 2-3) температура газа повышается от Т1 до комнатной (Т0), а давление газа повышается от атмосферного (Р0) до Р2. Применяя третье уравнение Пуассона (40) для описания адиабатического расширения газа (кривая 1-2)
Рисунок 8 – Диаграмма газовых процессов
и уравнение Шарля для изохорического нагревания (кривая 2-3)
,
и решая совместно эти уравнения можно получить расчетную формулу для определения коэффициента Пуассона по методу Клемана-Дезорма:
(41)
где: Р1 = Р0 + ΔР1; а Р2 = Р0; Р3 = Р0 + ΔР2; (42)
ΔР1 и ΔР2 – это избыточное давление газа.
Избыточное давление ΔР в методе Клемана-Дезорма измеряется водяным манометром:
ΔР1 = ρgΔh1 и ΔР2 = ρgΔh2, (43)
где ρ – плотность жидкости в водяном манометре;
g – ускорение свободного падения;
Δh = h2 - h1 – разность уровней воды в коленах манометра.
Подставляя (42) и (43) в формулу (41) окончательно получаем расчетную формулу для коэффициента Пуассона
, (44)
где Δh1 – разность уровней манометра в точке 1 до начала адиабатического расширения;
Δh2 - разность уровней манометра в точке 3 в конце изохорического нагревания.
Экспериментальная установка
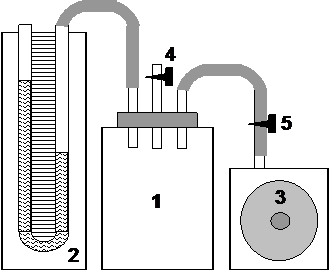Экспериментальная установка (рисунок 9) состоит из стеклянного баллона (1), водяного манометра (2), насоса (3), выпускного крана (4) и крана, отсекающего насос от баллона (5). Для осуществления адиабатического процесса сначала с помощью насоса создают в баллоне избыточное давление Р1 = Р0 + ΔР1, накачивая его в баллон. Адиабатическое расширение воздуха осуществляют путем кратковременного открывания выпускного крана (4) для быстрого понижения давления в сосуде до атмосферного Р0.
Рисунок 9 – Экспериментальная установка
| |
Экспериментальная часть
Задани е. Методом Клемана-Дезорма измерить коэффициент Пуассона
для воздуха.
1 Закрыть выпускной кран (4) и открыть кран, соединяющий насос с баллоном (5).
2 Медленно накачать воздух в баллон до момента почти полного поднятия правого уровня воды в манометре. Закрыть кран на насосе (5).
3 Выждать 2-3 минуты до выравнивания температуры газа в баллоне с окружающей средой и измерить Δh1 (записать в таблицу).
4 Открыть выпускной кран (4) на короткое время до выравнивания уровней жидкости в коленах манометра и закрыть этот кран (адиабатическое расширение).
5 Выждать 3-5 минут до выравнивания температуры в баллоне с окружающей средой (изохорическое нагревание).
6 После изохорического нагревания измерить разность уровней водяного манометра Δh2.
7 Повторить эксперимент (пункты 1- 6) не менее 4х раз. Результаты эксперимента записать в таблицу.
8 По формуле (44) вычислить коэффициент Пуассона для каждого опыта и вычислить его среднее значение. Вычислить абсолютную и относительную ошибки эксперимента.
Таблица 6– Результаты измерений
| № | Δh1 | Δh2 | γ | Δ γ | 
|
| 1 |
| ||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| γср = | Δ γср = |
Вопросы для допуска к работе
1 Что называется коэффициентом Пуассона?
2 Что называется адиабатическим процессом?
3 В чем суть метода Клемана-Дезорма?
Вопросы для зачета
1 Дать понятие теплоемкости (удельной и молярной). Вывести формулы для 
.
2 Адиабатический процесс. Уравнения Пуассона.
Литература
Трофимова, Т.И. Курс физики: учеб. пособие для вузов – 18-е изд., стереотип. – М.: Академия, 2010. – 560 с.
ЛАБОРАТОРНАЯ РАБОТА № 6
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ДИНАМИЧЕСКОЙ
ВЯЗКОСТИ ВОЗДУХА
Цель работы: Определить экспериментально и рассчитать теоретически
коэффициент динамической вязкости воздуха.
Теоретическое введение
Хаотическое движение молекул ведет к непрерывному перемешиванию газа. С этим связан ряд важных физических явлений, называемых явлениями переноса. Одно из них изучается в данной лабораторной работе.
Физическое явление вязкость. Возникновение сил трения между слоями газа, движущимися с различной скоростью, обусловленное переносом молекулами газа из слоя в слой своего импульса (количества движения), называется внутренним трением или вязкостью.
Численное значение силы внутреннего трения определяется по закону Ньютона для вязкости:
, (45)
где Fтр – сила внутреннего трения между слоями газа, движущимися с различными скоростями;
η - коэффициент внутреннего трения или коэффициент динамической вязкости;
- градиент скорости слоев газа;
S – площадь соприкасающихся слоев газа.
Молекулярно-кинетическая теория устанавливает связь коэффициента внутреннего трения с характеристиками хаотического движения молекул – средней скоростью движения и средней длиной свободного движения:
, 
(46)
где ρ – плотность газа; 
- средняя длина свободного пробега молекул газа;
- средняя арифметическая скорость хаотического движения молекул.
Средней длиной свободного пробега молекул называется статистически усредненный путь, проходимый молекулой между двумя последовательными столкновениями. Теория показывает, что все величины, входящие в формулу (46) могут быть вычислены по макроскопическим параметрам состояния газа – давлению (Р) и температуре (Т):
, (47)
где к – постоянная Больцмана;
d - эффективный диаметр молекул газа.
, (48)
где R – универсальная газовая постоянная;
μ – молярная масса.
, (49)
где Р, Т, μ, R – те же, что и в формулах (47), (48).
Таким образом, измеряя Р и Т воздуха, можно, пользуясь формулами (46), (47), (48), (49) вычислить теоретическое значение коэффициента динамической вязкости.
Идея эксперимента
Основная идея экспериментального определения коэффициента динамической вязкости газа заключается в создании условий для движения слоев газа и изучении последствий возникающей при этом силы трения между слоями газа.
Это условие реализуется следующим образом: в сосуде, соединенном с атмосферой тонкой трубкой, создается пониженное давление газа.
В газе, втекающем в сосуд по трубке, создаются движущие слои. Трение между слоями затрудняет втекание в сосуд, что приводит к установлению постоянной разности давлений газа в атмосфере и внутри сосуда (Δρ). Применяя закон Ньютона для вязкости, Пуазейль теоретически показал, что объем газа, протекающего по трубке, будет зависеть от разности давлений газа в начале и конце трубки по формуле:
, (50)
где V – объем газа, протекающего за время t;
ΔР – постоянная разность давлений на концах трубы;
r – радиус трубы;
– длина трубы;
η – коэффициент вязкости.
Для коэффициента вязкости из этой формулы получим расчетную формулу для экспериментального определения η
(51)
