Основными элементами установки (рисунок 7) являются эксикатор, водяной манометр  и медицинский шприц.
и медицинский шприц.
Эксикатор состоит из корпуса 1, крышки 2 и отводной трубки 4. Благодаря масляной прослойке между корпусом и крышкой, достигается хорошая герметичность эксикатора. Он служит сосудом, в который помещается исследуемое сыпучее вещество.
Стеклянные трубки 5 и 6 манометра соединены между собой резиновым шлангом 7.
Рисунок 7 – Экспериментальная установка
Роль поршня выполняет медицинский шприц 2. Шкала (3) служит для отсчета разности уровней воды в коленах манометра (Δh).
Внимание! Чтобы сохранить масляную прослойку на крышке и корпусе эксикатора, крышка должна быть или на корпусе эксикатора, или на специальной подставке. Ни в коем случае ею нельзя касаться поверхности стола. При помещении сыпучего вещества в эксикатор избегать случайного попадания вещества на масляную прослойку.
*Для ликвидации воздушных слоев в масляной прослойке при закрывании крышки нужно осторожно сделать несколько сдвигов крышки в разные с стороны в плоскости прослойки.
Экспериментальная часть
Задание. Измерить плотность сыпучих тел (песка или гравия).
Поместить вспомогательный сосуд без вещества в эксикатор и, не
Закрывая его крышкой герметично (крышка несколько сдвинута
относительно основного положения), установить одинаковые уровни в
коленах манометра. Затем закрыть крышку эксикатора.
2 Увеличить объем эксикатора, перемещая поршень шприца на 20 мл.
По шкале манометра измерить разность уровней Δ h1. Опыт по
измерению Δh1 проделать не менее трех раз и среднее значение записать
в таблицу 5.
3 Насыпать во вспомогательный сосуд исследуемое вещество, поместить
вещество в эксикатор и определить разность уровней воды в коленах
манометра Δh2 таким же образом, как Δ h1 (п.2).
4 По формуле (33) вычислить плотность сыпучего вещества. Значение Р0
определить по барометру, ρ в = 1000 кг/м 3.
5 Вычислить относительную и абсолютную погрешности измерения
плотности исследования веществ.
Таблица 5 – Результаты измерений
| m0, кг | Δh1, м | Δh2, м | р0, Па | ΔV м3 | 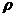 х, кг/м х, кг/м
|
| 105 | 2 · 10 -5 | ||||
Контрольные вопросы
1 Что представляет собой модель идеального газа, при каких условиях реальный газ можно считать идеальным газом?
2 Сформулировать законы идеального газа (изопроцессы).
3 Записать уравнение состояния идеального газа (уравнение Клайперона – Менделеева) и вывести из него уравнение Больцмана.
4 Что такое плотность вещества?
5 В чем суть предложенного метода определения объема сыпучего или пористого вещества?
Литература
1 Грабовский Р. И. Курс физики: учеб. пособие – 2-е изд., стереотип. – СПб.: Лань, 2012. – 608 с.: ил.
2 Трофимова Т. И. Курс физики: учеб. пособие для вузов – 18-е изд., стереотип. – М.: Академия, 2010. – 560 с.
ЛАБОРАТОРНАЯРАБОТА№5
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПУАССОНА ДЛЯ ВОЗДУХА
Цель работы
Экспериментальное определение коэффициента Пуассонаметодом Клемана-Дезорма.
Теоретическое введение
Коэффициентом Пуассона ( ) называется отношение молярной (или удельной) теплоемкости газа при постоянном давлении (Ср) к теплоемкости газа при постоянном объеме (СV):
) называется отношение молярной (или удельной) теплоемкости газа при постоянном давлении (Ср) к теплоемкости газа при постоянном объеме (СV):
 (34)
(34)
Удельная теплоемкость (С) – это скалярная величина, равная количеству теплоты, необходимому для повышения температуры единицы массы вещества на один градус:

 (35)
(35)
Молярная теплоемкость (См) – это скалярная величина,равнаяколичеству теплоты, необходимому для повышения на один градус:
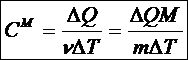
 , (36)
, (36)
где: 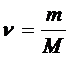 - число молей вещества.
- число молей вещества.
По формуле первого начала термодинамики:
 , (37)
, (37)
где ΔQ – количество теплоты;
Δu – изменение внутренней энергии;
А – работа, совершаемая системой,
можно в рамках молекулярно-кинетической теории идеального газа вычислить теоретически молярные теплоемкости газа при изобарном  и изохорном
и изохорном  нагревании газа:
нагревании газа:
 и
и  , (38)
, (38)
где i-число степеней свободы молекулы газа;
R-универсальная газовая постоянная.
Коэффициент Пуассона можно рассчитать теоретически, подставив (5) в формулу (1):

 (39)
(39)
Коэффициент Пуассона является одним из параметров, характеризующих адиабатический газовый процесс. Адиабатический процесс – это изменение состояния газовой системы, происходящее без теплообмена с окружающей средой (Δ Q = 0).
Макропараметры газовой системы (V, Р, Т) при адиабатическом процессе связаны между собой уравнениями Пуассона:
 ;
;  ;
;  (40)
(40)
Из второго уравнения Пуассона следует, что при адиабатическом расширении газа его температура понижается. Это свойство адиабатического процесса используется при экспериментальном определении коэффициента Пуассона методом Клемана – Дезорма.
Адиабатический процесс можно осуществить двумя способами: либо в теплоизолированном сосуде, либо в неизолированном, но очень быстро.






