АААА
А саны  ұмтылғандағы
ұмтылғандағы  функциясының шегі деп аталады, егер кез келген
функциясының шегі деп аталады, егер кез келген 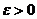 саны үшін
саны үшін 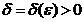 саны табылып,
саны табылып,  теңсіздігін қанағаттандыратын барлық
теңсіздігін қанағаттандыратын барлық  үшін келесі теңсіздік орындалса: A)
үшін келесі теңсіздік орындалса: A)  .; B)
.; B)  .; C)
.; C)  .
.
А саны  ұмтылғандағы
ұмтылғандағы  функциясының шегі деп аталады, егер кез келген
функциясының шегі деп аталады, егер кез келген 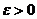 саны үшін
саны үшін 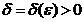 саны табылып,
саны табылып,  теңсіздігін қанағаттандыратын барлық
теңсіздігін қанағаттандыратын барлық  үшін келесі теңсіздік орындалса: B)
үшін келесі теңсіздік орындалса: B)  ;E)
;E)  .;H)
.;H)  .
.
А жәнеВ жиындарыныңқиылысуыдеп C)Ажәне В жиындарынатиістіболатын  жиынынайтамыз.
жиынынайтамыз.
А жәнеВ жиындарыныңбірігуідеп E)Анемесе В жиындарыныңеңолмағандабіреуінетиістіболатын  жиынынайтамыз.
жиынынайтамыз.
Анықталмаған интеграл үшін дұры формулалар D) ∫  ; F) ∫cosxdx = sinx+C
; F) ∫cosxdx = sinx+C




ББББ
Бірінші ретті туындының физикалық мағынасы: C) функцияның өзгеру жылдамдығы.
ДДДД
Дифференциалдаудың ережелері мына теңдіктермен беріледі: D)  ; E)
; E) 
ЕЕЕЕ
Егер  и
и  , где
, где  , то: A)
, то: A) 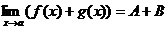 .; B)
.; B)  .; C)
.; C)  .
.
Егер  болса, онда
болса, онда  туындының мәні келесі аралыққа тиісті болады: D)
туындының мәні келесі аралыққа тиісті болады: D)  .; E)
.; E)  .; G)
.; G)  .
.
Егер 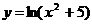 болса, онда
болса, онда  туындының мәні келесі аралыққа тиісті болады: D)
туындының мәні келесі аралыққа тиісті болады: D)  .; G)
.; G)  .; H)
.; H) 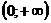 .
.
Егер 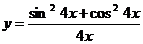 , онда
, онда  = E)
= E)  .; F)
.; F) 
Егер  және
және  шектері бар болса, онда мына теңдіктер орынды болады: B)
шектері бар болса, онда мына теңдіктер орынды болады: B)  *
*  ; D)
; D)  ; E)
; E)  -
- 
КККК
Келесі пайымдаулардың қайсысы дұрыс?
Функциясының нүктесінде дифференциалдануы үшін осы нүктеде ақырлы туындының бар болуы қажетті және жеткілікті.
Егер функциясықандай да бір нүктеде дифференциалданатын болса, онда ол осы нүктеде үзіліссіз.
Егер функциясының қандай да бір нүктеде туындысы бар болса, ондаол осы нүктеде үзіліссіз.
4. Егер  функциясының қандай да бір нүктеде үзіліссіз болса, ондаол осы нүктеде дифференциалданады. D) 1, 2, 3.
функциясының қандай да бір нүктеде үзіліссіз болса, ондаол осы нүктеде дифференциалданады. D) 1, 2, 3.
Келесі теңдіктер орынды: A)  .; B)
.; B)  ,
,  .; C)
.; C) 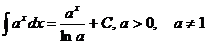 .
.
Келесі теңдіктер орынды: B)  ,
,  .; C)
.; C) 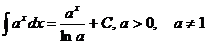 .; D)
.; D)  .
.
Келесі теңдіктер орынды: C) 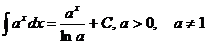 .; D)
.; D)  .; E)
.; E)  .
.
Келесі теңдіктер орынды: D)  .; E)
.; E)  . F)
. F) 
 ,
,  .
.
Келесі теңдіктер орынды: E)  . F)
. F) 
 ,
,  .; G)
.; G)  .
.
Келесі теңдіктер орынды: F) 
 ,
,  .; G)
.; G)  .; H)
.; H)  .
.
Келесі теңдіктер орынды: A)  .; G)
.; G)  .; H)
.; H)  .
.
Келесі теңдіктер орынды: A)  .; B)
.; B)  ,
,  .; H)
.; H) 
МММ
 нүктедегі
нүктедегі  қисығына жүргізілген жанаманың теңдеуі: A)
қисығына жүргізілген жанаманың теңдеуі: A) 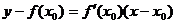 .
.
ТТТТ
Туындының геометриялық мағынасы: C)  , мұнда
, мұнда  – жанама мен
– жанама мен  осінің арасындағы бұрыш.
осінің арасындағы бұрыш.
Dx нөлге ұмтылғандағы Dу=f(x0+ Dx)-f(x0) функция өсімшесінің Dx аргумент өсімшесіне қатынасы B)f(x) функциясының туындысы деп аталады.
 функциясы үшін
функциясы үшін  нүктесі: Нүктеде функция анықталмайды; Үзіліс нүктесі; ІІ текті үзіліс нүктесі
нүктесі: Нүктеде функция анықталмайды; Үзіліс нүктесі; ІІ текті үзіліс нүктесі
\\  функцисыяның екінші ретті туындысы:
функцисыяның екінші ретті туындысы:
E)  .
.
\\  , мұндағы
, мұндағы 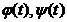 - дифференциалданатын функциялар, параметрмен берілген функцияның туындысы:
- дифференциалданатын функциялар, параметрмен берілген функцияның туындысы:
C)  .
.
\\ 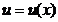 болса, онда
болса, онда  функциясының туындысы:
функциясының туындысы:
E)  .
.
\\ 
B)  .
.
E)  .
.
\\  функциясыүшін
функциясыүшін 
E) 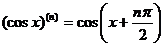 .
.
y=sinx+cosx функциясының туындысы:
A) 
B) 
y(x)=x*ctgx функциясының туындысы:
B) 
D) 
E) 
y=  функциясының туындысы:
функциясының туындысы:
С) 
F) 
lim
\\ 
A) 0.
F)  .
.
\\ 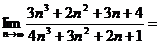
D)  .
.
\\  =
=
A) e2
F)  .
.
\\ 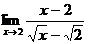 =
=
C) 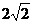 .
.
G)  .
.
\\ 
C)  .
.
D)  .
.
\\  =
=
A)  .
.
H)  .
.
\\  =
=
C) -0.6.
F)  .
.
\\  =
=
B)  .
.
C) 3.
F)  .
.
\\  =
=
C) 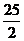 .
.
D) 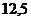 .
.
F)  .
.
Шегінің мәні келесі аралыққа тиесілі
D)  .
.
E)  .
.
H) 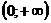 .
.
Шегінің мәні келесі аралыққа тиесілі
E)  .
.
G)  .
.
H) 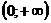 .
.
\\ 
A)  .
.
B)  .
.
C)  .
.
\\ 
D)  .
.
E)  .
.
\\ 
A) 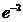 .
.
C) 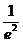 .
.
H)  .
.
шегінің мәні келесі аралыққа тиесілі
D)  .
.
E)  .
.
G)  .
.
\\  шегі тең:
шегі тең:
C) 
G) 4
 шегі тең:
шегі тең:
A) 
C) 0
E) ln1
 шегі тең:
шегі тең:
B) 
F) 4
 шегі тең болатын сан:
шегі тең болатын сан:
C) 
E) ln 
 табылған шектің жатқан аралығы:
табылған шектің жатқан аралығы:
С) (-  ,4]
,4]
 табылған шек жатқан аралығы:
табылған шек жатқан аралығы:
D) (-3,-1)
E) [-3,0]
G) (-  ]
]
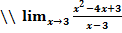 табылған шектің жатқан аралығы:
табылған шектің жатқан аралығы:
A) (1,4)
E) (- 
G) [1,4]
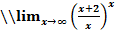 шегі тең болатын сан:
шегі тең болатын сан:
B) 
E) 
F)  ln e
ln e

C) 1
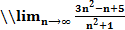 шегі тең болатын сан:
шегі тең болатын сан:
C) ln 
E) 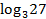
F) 3
 шегі тең:
шегі тең:
B) 1
D) 
F) lne
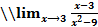 табылған шектің жатқан аралығы:
табылған шектің жатқан аралығы:
C) (-∞,4]
D) (0,4)
 шегі тең болатын сан:
шегі тең болатын сан:
A) ln 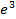
 табылған шектің жатқан аралығы:
табылған шектің жатқан аралығы:
A) (-∞,4]
D) [-4,4]
E) (-4,4)

A) 
C) 
 шегі тең:
шегі тең:
C) 
E)  *lne
*lne
F) 
 шегі тең:
шегі тең:
B) 
D) 
E) ∞





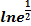 ;
; 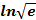

 ;3
;3 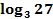
 (
(  ; [-4;4] [4;6]
; [-4;4] [4;6]
 5/0; 1/0;
5/0; 1/0; 

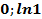




 :
: 
 : 12/18; 2/3;
: 12/18; 2/3; 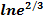
 :
: 
 :
: 
 :
: 
 :
: 
 : [1:4]; (1:4); (-
: [1:4]; (1:4); (-  )
)
y=


 [
[  ]
]
 :
:  ;
;  ;
; 


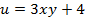 функциясының
функциясының  дербес туындысының
дербес туындысының  : (
: (  (-4;4) (-5;5)
(-4;4) (-5;5)
 (-30;30); (-25;25); (
(-30;30); (-25;25); ( 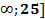
 :
: 
 функциясы үшін
функциясы үшін  нүктесі: Нүктеде функция анықталмайды; Үзіліс нүктесі; ІІ текті үзіліс нүктесі
нүктесі: Нүктеде функция анықталмайды; Үзіліс нүктесі; ІІ текті үзіліс нүктесі
 : (-1/2;+
: (-1/2;+  )- өсу аралығы; (-
)- өсу аралығы; (-  )-кему аралығы; x =-1/2 максимум
)-кему аралығы; x =-1/2 максимум
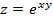 :
: 


 :
: 
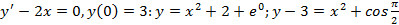 ;
;
 :
: 
 (0
(0  ); (0
); (0  )
)

\\  функцияныңанықталуоблысы:
функцияныңанықталуоблысы:
B)  или
или  .
.
\\  функцияныңанықталуоблысы:
функцияныңанықталуоблысы:
C)  или
или  .
.
\\  функцияның үзіліс нүктелері:
функцияның үзіліс нүктелері:
B) х1=1, х2=5.


 [
[  ]
]
\\  функцияның үзіліс нүктелері:
функцияның үзіліс нүктелері:
B)функцияүзіліссіз.
\\  функцияның туындысы:
функцияның туындысы:
A)  .
.
B) 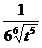 .
.
E)  .
.
\\  функцияның туындысы:
функцияның туындысы:
A)  .
.
B)  .
.
F) 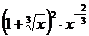 .
.
\\  функцияның туындысы:
функцияның туындысы:
C)  .
.
D)  .
.
G)  .
.
\\  функцияның туындысы:
функцияның туындысы:
B)  .
.
G)  .
.
H)  .
.
\\ 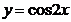 функци яның дифференциал ы:
функци яның дифференциал ы:
B)  .
.
D) 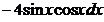 .
.
F)  .
.
\\  функциясының екінші ретті туындысы:
функциясының екінші ретті туындысы:
B)  .
.
C)  .
.
F)  .
.
\\  функциясының бесінші ретті туындысы:
функциясының бесінші ретті туындысы:
B) 5!.
D)  .
.
H)  .
.
\\  функциясының туындысы:
функциясының туындысы:
D) 
\\  функциясының екінші реттітуындысы:
функциясының екінші реттітуындысы:
A)  .
.
G)  .
.
\\  функциясының екінші ретті туындысы:
функциясының екінші ретті туындысы:
B)  .
.
F)  .
.
\\  функциясының алғашқы бейнесі:
функциясының алғашқы бейнесі:
C)  .
.
E)  .
.
\\  функциясының алғашқы бейнесі:
функциясының алғашқы бейнесі:
C)  .
.
E)  .
.
\\ 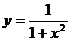 функциясының алғашқы бейнесі:
функциясының алғашқы бейнесі:
D)  .
.
F)  .
.
\\y= 

B) 0 ≤ S < 2
 Коши есебінің шешімі:
Коши есебінің шешімі:
A) y=3 + 
C) y=  + 2 +
+ 2 + 
F) y- 3=  + cos
+ cos 
 (0
(0  ); (0
); (0  )
)

 - 4y' +13y=0 теңдеуінің шешімі:
- 4y' +13y=0 теңдеуінің шешімі:
D) y= 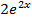 cos3x+5
cos3x+5  sin3x
sin3x
E) y= 
F)`y= 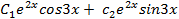
\\y'=  , y(0)=8 Коши есебінің шешімі:
, y(0)=8 Коши есебінің шешімі:
B) lny = ln2+ln|x+4|
D) y= 
 -
-  =0 теңдеуінің шешімі:
=0 теңдеуінің шешімі:
A) y=3+2x+ 
G) y=  +
+  +
+ 
 функциясы үшін
функциясы үшін 
B)  .
.
F)  .
.
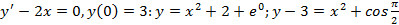 ;
;
 :
: 
 (0
(0  ); (0
); (0  )
)

f
\\  функциясының
функциясының  нүктесіндегі туындысы:
нүктесіндегі туындысы:
A) 0.
F)  .
.
\\ 

 функциясының
функциясының  нүктесіндегі туындысы:
нүктесіндегі туындысы:
C) 2.
D)  .
.
G)  .
.
\\  функциясы үшін мына тұжырым дұрыс:
функциясы үшін мына тұжырым дұрыс:
A) (5,+  ) – өсу аралығы
) – өсу аралығы
D)(-  ) – кему аралығы
) – кему аралығы
\\  - екінші ретті дербес туындының
- екінші ретті дербес туындының 
C) (-1,1)
D) (-  ]
]
E) (-5,3)
\\ f(x) = 
C) y'=3  +4
+4
\\  :
:  ;
;  ;
; 


\\f=2x  функциясының
функциясының  екінші ретті туындысының
екінші ретті туындысының  нүктесіндегі мәні мына аралықта жатады:
нүктесіндегі мәні мына аралықта жатады:
C) (-25,25)
F) (-30,30) ( 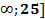
Анықталмаған интеграл
\\ 
A)  .
.
\\ 
B)  .
.
F)  .
.
\\ 
B) 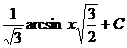 .
.
\\ 
C)  .
.
\\ 
C)  .
.
G)  .
.
\\ 
D)  .
.
H)  .
.
\\ 
A)  .
.
C)  .
.
\\ 
C)  .
.
E)  .
.
\\ 
E)  .
.
\\ 
C)  .
.
G)  .
.
\\ 
C)  .
.
\\ 
D) 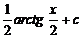 .
.
\\ 
A) 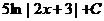 .
.
F) 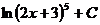 .
.
\\ 
B)  .
.
G)  .
.
\\ 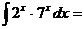
C)  .
.
\\ 
D)  .
.
\\ 
B)  .
.
D)  .
.
\\ 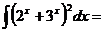
A)  .
.
C)  .
.
\\ 
B)  .
.
E)  .
.
H)  .
.
\\ 
A)  .
.
E)  .
.
\\ 
C) C -  cos(2x+3)
cos(2x+3)
\\ 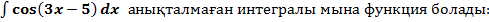
A) 
D) 
E) 
\\  анықталмаған интегралдың алғашқы функциялары:
анықталмаған интегралдың алғашқы функциялары:
B) 
E) 
\\  анықталмаған интегралдың алғашқы функциялары:
анықталмаған интегралдың алғашқы функциялары:
B) 
C) 
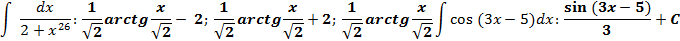


Анықталған интеграл
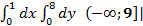 (-9;9);[-9;9]|
(-9;9);[-9;9]|





\\ 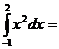
C) 3.
\\ 
A)  .
.
C)  .
.
D)  .
.
\\ 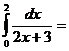
A)&  .
.
B) 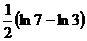 .
.
C)  .
.
\\ 
A)  .
.
\\ 
B)  .
.
\\ 
C)  .
.
G)  .
.
\\ 
D)  .
.
H)  .
.
\\ 
E)  .
.
\\ 
A)  .
.
C)  .
.
F)  .
.
\\ 
B)  .
.
D)  .
.
H)  .
.
\\ 
A)2/7.
\\ 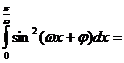
B)  .
.
\\ 
C)  .
.
\\ 
A)  .
.
C)  .
.
\\  интегралының мәні мына аралықта жатады:
интегралының мәні мына аралықта жатады:
D) [-9,9]
\\ 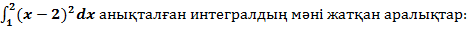
A) (-  ]
]
B) (-1,1)
 анықталған интегралдың мәні жатқан аралықтар:
анықталған интегралдың мәні жатқан аралықтар:
A) (-5,3)
B) (-1,1)
\\ 
D) (-∞,4)
E) [-4,4]
\\  анықталған интегралдың мәні жатқан аралықтары:
анықталған интегралдың мәні жатқан аралықтары:
A) (-∞,2]
B) (-5,3)
C) (-1,1)
 анықталған интегралдың мәні жатқан аралықтар:
анықталған интегралдың мәні жатқан аралықтар:
B) (-5,8)
C) (-∞,3]
F) (-3,3)
\\ 
C)  .
.
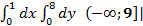 (-9;9);[-9;9]|
(-9;9);[-9;9]|





Рационал бөлшек
 рационал бөлшекті келесі қарапайым бөлшектердің қосындысы түрінде жазуға болады:
рационал бөлшекті келесі қарапайым бөлшектердің қосындысы түрінде жазуға болады:
B)  .
.
C) 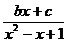 .
.
D)  .
.
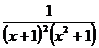 рационал бөлшекті келесі қарапайым бөлшектердің қосындысы түрінде жазуға болады:
рационал бөлшекті келесі қарапайым бөлшектердің қосындысы түрінде жазуға болады:
A)  .
.
C)  .
.
E)  .
.
 рационал бөлшекті келесі қарапайым бөлшектердің қосындысы түрінде жазуға болады:
рационал бөлшекті келесі қарапайым бөлшектердің қосындысы түрінде жазуға болады:
B)  .
.
D)  .
.
F)  .
.
 рационал бөлшекті келесі қарапайым бөлшектердің қосындысы түрінде жазуға болады:
рационал бөлшекті келесі қарапайым бөлшектердің қосындысы түрінде жазуға болады:
C)  .
.
E)  .
.
G)  .
.
\\ 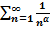 , (
, (  ) сандық қатары үшін мына тұжырым дұрыс болады:
) сандық қатары үшін мына тұжырым дұрыс болады:
B) 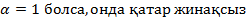
E) 
 B) (2n-1)
B) (2n-1) 
\\z =  функциясы үшін дұрыс қатынастар:
функциясы үшін дұрыс қатынастар:
A) 
D) 
G) 
\\






