Цель работы: исследование электрических цепей синусои- дального тока с последовательным, параллельным и смешанным соединением элементов.
Общие сведения
Энергетические процессы в цепях синусоидального тока харак- теризуется активной Р, реактивной Q, полной S и комплексной
|

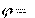
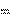 Активная мощность Р соответствует электроэнергии, которая необратимо преобразуется в другой вид энергии в активном при- емнике и определяется соотношением:
Активная мощность Р соответствует электроэнергии, которая необратимо преобразуется в другой вид энергии в активном при- емнике и определяется соотношением:
| P I 2 R UI cos Re U I; P Вт. | (2.1) |
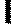
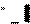
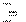
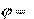

 Реактивная мощность Q характеризует энергию, которой обме- ниваются генератор и приемник:
Реактивная мощность Q характеризует энергию, которой обме- ниваются генератор и приемник:
| Q I 2 X UI sin Im U I; Q ВАр. | (2.2) |
10
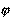



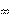 Полная мощность S соответствует той мощности, которую ис- точник может отдавать потребителю, если последний будет рабо- тать при cos = 1:
Полная мощность S соответствует той мощности, которую ис- точник может отдавать потребителю, если последний будет рабо- тать при cos = 1:
S U 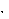 I I 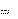 P 2 Q 2; S ВА. P 2 Q 2; S ВА.
| (2.3) |
|

В цепи (рис. 2.1, а), содержащей активное сопротивление RL и индуктивность L, вектор активного напряжения UR совпадает с вектором тока, вектор индуктивного напряжения UL опережает ток на угол 90° (рис. 2.1, б).
|
| |||
| а | б | в | г |
| Рис. 2.1 | |||
|
| |||
| а | б | в | г |
| Рис. 2.2 | |||
На основе векторной диаграммы (рис. 2.1, б) можно построить треугольники сопротивлений (рис. 2.1, в) и мощностей (рис. 2.1, г). Все эти треугольники подобны, причем в противоположность век- торной диаграмме треугольники мощностей и сопротивлений со- стоят из отрезков, а не векторов, так как сопротивления и мощно- сти – скалярные величины.
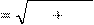 Полное сопротивление цепи:
Полное сопротивление цепи:
| (2.5) |
11
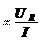 г д е R L
г д е R L
– активное сопротивление, а X L
– индуктив-
ное сопротивление.
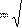

 Полная мощность цепи:
Полная мощность цепи:
| S U I P 2 Q 2 , L | (2.6) |
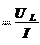 где
где
P 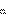 U R
U R 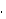 I
I
– активная мощность; Q L
U L 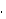 I
I
– индуктивная мощ-
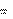 ность.
ность.
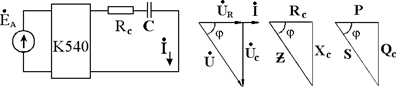
В неразветвленной цепи, содержащей активное сопротивление RC и емкость С (рис. 2.2, а), вектор активного напряжения UR сов- падает с вектором тока, а вектор емкостного напряжения UС отста- ет от тока на угол 90° (рис. 2.2, б). Треугольники сопротивлений и мощностей для такой цепи приведены на рис. 2.2, в, г. Полное со- противление цепи, а также мощность определяются аналогично со- отношениям, приведенным для предыдущей схемы с последова- тельным соединением RL и L.
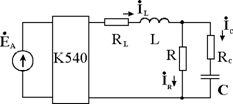 Рис. 2.3
Рис. 2.3
| В случае смешанно- го соединения элемен- тов (рис. 2.3) применя- ется символический ме- тод расчета цепей сину- соидального тока. При этом последователь- ность расчета такая же, как для цепи постоян- ного тока. |
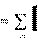

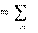
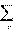 По результатам расчета строится векторная диаграмма цепи. В схеме должен соблюдаться баланс мощностей:
По результатам расчета строится векторная диаграмма цепи. В схеме должен соблюдаться баланс мощностей:
| ~ n * * n 2 2 2 S (E K I K U K J K ) I K R K K 1 K 1 | (2.7) | |||
| где | n E K I * K K 1 | – |
сумма мощностей источников ЭДС; | |
| n U K J * K K 1 | – | сумма мощностей источников тока; | ||
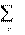 12
12
| n I 2 R K K K 1 | – | сумма мощностей активных элементов цепи; |
| n jI 2 (X X) K LK CK K 1 | – | сумма мощностей реактивных элементов цепи. |
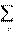
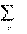
 Программа работы
Программа работы
1. Собрать схему рис. 2.1, а, замерить величины I, U, P, резуль- таты занести в табл. 2.1.
2. Собрать схему рис. 2.2, а, измерить комплектом K540 I, U, P
в цепи, полученные результаты записать в табл. 2.1.
3. Собрать схему рис. 2.3; замерив значения I, U, P по комплек- ту K540, занести результаты в табл. 2.1.
4. Используя результаты эксперимента (п.п. 1 и 2), рассчитать параметры схем замещения катушки RL и L и конденсатора RC и C. Результаты занести в табл. 2.1.
5. Построить в масштабе векторные диаграммы для схем рис. 2.1, а и рис. 2.2, а, треугольники сопротивлений (схема рис. 3.1, а), прово- димостей (схема рис. 2.2, а), мощностей (рис. 2.1, а и 2.2, а).
6. По известным параметрам RL, L, RC, C, R рассчитать все то- ки, напряжения на всех элементах и всех ветвях в схеме рис. 2.3.
По результатам расчета построить векторную диаграмму. Оп- ределить мощности P, Q, S всех ветвей и всей цепи. Составить ба- ланс мощностей. Сравнить результаты расчета с экспериментом (P, I, определенные с помощью K540).
Таблица 2.1
| Эксперимент | Расчет | ||||||||||
| U, B | I, A | P, Вт | R L(C), Ом | S, BА | Z, Ом | Q, BAp | XL, Ом | L, Гн | ,º | XC, Ом | C, Ф |
| – | – | ||||||||||
| – | – | ||||||||||
| – | – | – | – | – | – | – | – | – | |||
13

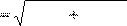
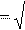
 Р а с ч е т н ы е ф о р м у л ы
Р а с ч е т н ы е ф о р м у л ы
| P L (С) R L (С) 2 ; I L (С) | (2.1’) |
| (2.5’) | |
| S U I P 2 Q 2; L (С) | (2.6’) |
| X L(С) L (С ) arctg R ; L(С) | (2.8) |
| L X L; | (2.9) |
| C 1 . X C | (2.10) |


 Сод ер жание о тчета:
Сод ер жание о тчета:
– схемы рис. 2.1, а, 2.2, а, 2.3;
– табл. 2.1;
– расчеты и графические построения согласно п.п. 4, 5, 6;
– выводы.
Варианты заданий
Таблица 2.2
| № варианта | Катушка индуктивности | Резистор | Конденсатор |
| 1 | L1 | R = 10 Ом | С = 40 мкФ |
| 2 | L1 | R = 50 Ом | С = 50 мкФ |
| 3 | L1 | R = 30 Ом | С = 70 мкФ |
| 4 | L1 | R = 10 Ом | С = 90 мкФ |
| 5 | L1 | R = 50 Ом | С = 120 мкФ |
| 6 | L1 | R = 10 Ом | С = 150 мкФ |
Контрол ь ные вопр о сы
1. Чему равно индуктивное сопротивление, и в каких единицах оно измеряется? Емкостное сопротивление?
14
2. Каким образом можно изменить индуктивное сопротивле- ние? Емкостное сопротивление? Их физическая сущность?
3. Что такое активная и реактивная мощности однофазной цепи переменного тока и в каких единицах их измеряют?
4. Чему равна полная мощность однофазной цепи переменного тока и в каких единицах ее измеряют?
5. Что такое коэффициент мощности?
6. Как рассчитать проводимость для параллельного соединения резистора и идеального конденсатора?
7. Как строятся треугольники токов, проводимостей, мощно- стей для разветвленной цепи с активно-емкостной нагрузкой?
8. Как строятся треугольники напряжений, сопротивлений, мощностей для цепи с последовательно соединенными R и L?
9. Что произойдет, если катушку индуктивности, рассчитанную для работы в цепях переменного тока, включить в цепь постоянно- го тока с таким же значением напряжения?
10. Как строится векторная диаграмма цепи синусоидального тока со смешанным соединением элементов?
Л аборатор ная ра бот а № 3
Резонанс напряжений
Цель работы: исследовать частотные свойства электрических цепей и основные особенности режима резонанса при последова- тельном соединении индуктивной катушки и конденсатора.
Общие сведения
В электрических цепях переменного тока, содержащих ин- дуктивные и емкостные элементы, может возникать особый ре- жим работы, называемый режимом резонанса. Этот режим ха- рактеризуется тем, что входное сопротивление цепи является чисто активным, и, следовательно, входные ток и напряжения совпадают по фазе.
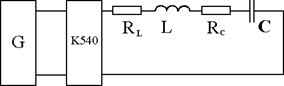
При последовательном соединении катушки индуктивности и конденсатора (рис. 3.1), когда их реактивные сопротивления XL и XC становятся равными друг другу, возникает резонанс напря- жений.
15
|
| Рис. 3.1 |
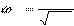 Равенство реактивных сопротивлений XL и XC (ωL = 1/ωC) мо- жет быть получено изменением емкости, индуктивности или часто- ты питающей сети. В данной работе явление резонанса достигается путем изменения частоты до резонансного значения
Равенство реактивных сопротивлений XL и XC (ωL = 1/ωC) мо- жет быть получено изменением емкости, индуктивности или часто- ты питающей сети. В данной работе явление резонанса достигается путем изменения частоты до резонансного значения
| 1. P LC | (3.1) |
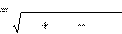 Действующее значение тока в исследуемой цепи (см. рис. 3.1) определяется выражением:
Действующее значение тока в исследуемой цепи (см. рис. 3.1) определяется выражением:
| I U , R 2 (X L X C)2 | (3.2) |
| где | U | – | напряжение на входе схемы; |
| R = RL + RC | – | активное сопротивление цепи. | |
Как видно из выражения (3.2), при резонансе ток в цепи дости- гает максимального значения, поскольку в этом случае полное со- противление цепи минимально: Z = R.
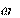
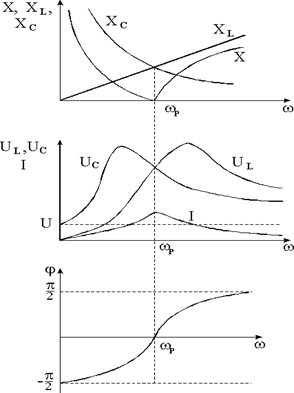
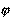 Зависимости от частоты (или f) действующих значений на- пряжений UL и UC, сопротивлений XL, XC и X, действующего зна- чения тока I, угла и других электрических величин и параметров, относящихся к данной цепи, называются ее частотными характери- стиками. Их примерный вид показан на рис. 3.2.
Зависимости от частоты (или f) действующих значений на- пряжений UL и UC, сопротивлений XL, XC и X, действующего зна- чения тока I, угла и других электрических величин и параметров, относящихся к данной цепи, называются ее частотными характери- стиками. Их примерный вид показан на рис. 3.2.
Программа работы
1. Собрать схему рис. 3.1.
2. Изменяя частоту источника питания (10–12 значений, вклю- чая fр), исследовать режимы работы цепи. Результаты измерений занести в табл. 3.1.
16
|
| Рис. 3.2 |
3. Используя данные измерений, рассчитать указанные в табл.
3.1 величины:
– 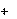
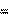 активное сопротивление цепи
активное сопротивление цепи
| R R L R C ; | (3.3) |
– 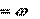 индуктивное сопротивление катушки
индуктивное сопротивление катушки
| X L L; | (3.4) |
–  емкостное сопротивление конденсатора
емкостное сопротивление конденсатора
| X 1; C C | (3.5) |
– 
 реактивное сопротивление цепи
реактивное сопротивление цепи
X 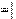 X L X C ; X L X C ;
| (3.6) |
17
– 
 индуктивное напряжение
индуктивное напряжение
| U L X L I; | (3.7) |
– 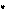
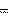 емкостное напряжение
емкостное напряжение
| U С X С I; | (3.8) |
– 
 величину угла
величину угла 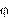
| arctg X L X C. R | (3.9) |
Примечание. Параметры схем замещения катушки индуктив- ности (RL и L) и конденсатора (RC и С) рассчитаны в лабораторной работе № 2.
4. По данным табл. 3.1 построить частотные характеристики цепи рис 3.1.
5.  Определить расчетным путем резонансную частоту и сравнить результат с экспериментом.
Определить расчетным путем резонансную частоту и сравнить результат с экспериментом.
6. Построить в масштабе векторные диаграммы исследуемой цепи для трех различных режимов:
– XL < XC;
– XL = XC;
– XL > XC.
 Таблица 3.1
Таблица 3.1
| № опыта | Эксперимент | Расчет | |||||||||
| f, Гц | U, B | I, A | P, Вт | R, Ом | XL, Ом | XC, Ом | Х, Ом | UL,B | UC, B | ,º | |
С о д е р ж а н и е о т ч е т а:
– схема исследуемой цепи (см. рис. 3.1);
– табл. 3.1;
– расчет и графические построения согласно п.п. 3, 4, 5, 6 про- граммы работы;
– выводы.
Варианты заданий
Таблица 3.2
| № варианта | Катушка индуктивности | Конденсатор |
| 1 | L1 | С = 40 мкФ |
| 2 | L1 | С = 50 мкФ |
| 3 | L1 | С = 70 мкФ |
| 4 | L1 | С = 90 мкФ |
| 5 | L1 | С = 120 мкФ |
| 6 | L1 | С = 150 мкФ |
18
Контрол ь ные вопр о сы и зад ания
1. Объясните, при каких условиях и в какой цепи возникает ре- зонанс напряжений. Каковы признаки возникновения резонанса напряжений?
2. В чем могут заключаться эксплуатационные опасности, свя- занные с явлением резонанса в реальных условиях и цепях?
3. Опишите энергетический процесс в цепи (см. рис. 3.1) при резонансе напряжений.
4. При каких условиях в цепи, содержащей катушку и конден- сатор, мог бы иметь место незатухающий колебательный процесс?
Л аборатор ная ра бот а № 4
Исследование процессов





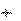 j Q Se j U I .
j Q Se j U I .
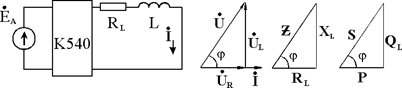
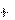 jI K (X LK X CK),
jI K (X LK X CK),
