Раздел I. Множества, функции, отношения.

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

«Тульский государственный университет»

Механико-математический факультет

Кафедра математического моделирования

В.В. Козлов

ЛЕКЦИИ ПО ДИСЦИПЛИНЕ

«Дискретная математика»

Учебное пособие

Разработал: В.В. Козлов, канд. физ.-мат. наук, ассистент

Содержание.

Лекция № 1. Множества и операции над ними.
Лекция № 2. Соответствия и функции.
Лекция № 3. Отношения и их свойства.
Лекция № 4. Основные виды отношений.
Лекция № 5. Элементы общей алгебры.
Лекция № 6. Различные виды алгебраических структур.
Лекция № 7. Элементы математической логики.
Лекция № 8. Логические функции.
Лекция № 9. Булевы алгебры.
Лекция № 10. Булевы алгебры и теория множеств.
Лекция № 11. Полнота и замкнутость.
Лекция № 12. Язык логики предикатов.
Лекция № 13. Комбинаторика.
Лекция № 14. Графы: основные понятия и операции.
Лекция № 15. Маршруты, цепи и циклы.
Лекция № 16. Некоторые классы графов и их частей.

РАЗДЕЛ I. МНОЖЕСТВА, ФУНКЦИИ, ОТНОШЕНИЯ.

Лекция № 1. Множества и операции над ними.

1. Основные понятия теории множеств.

Определение. Множеством М называется объединение в единое целое определенных различимых однотипных объектов а, которые называются элементами множества.

а Î М

Множество можно описать, указав какое-то свойство, присущее всем элементам этого множества.

Замечание. Вообще говоря, понятие множества считается первичным (исходным) понятием, и, как таковое, не определяется. Приведённое выше определение следует, скорее, считать уточнением понятия множества.

Множество, все элементы которого являются числами, называется числовым. В дальнейшем мы будем, прежде всего, рассматривать именно такие множества. Множество, элементами которого являются другие множества, называется классом или семейством.

Множество, содержащее конечное число элементов, называется конечным. При подсчёте количества элементов учитываются только различные (неповторяющиеся) элементы.

Множество, не содержащее элементов, называется пустым и обозначается символом Æ.

Множество может быть задано перечислением (списком) своих элементов, порождающей процедурой или описанием характеристических свойств (предикатом), которым должны обладать его элементы. Причём в последнем случае необходимо формулировать описание характеристических свойств элементов множества достаточно корректно, для того, чтобы множество было определено вполне однозначно. Добавим, что многие числовые множества могут быть заданы всеми тремя указанными способами (например, множество чётных однозначных чисел).

Пример 1. Некоторые примеры множеств, заданных различными способами.

а) .

б) .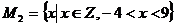

в) .

Мощностью конечного множества М называется количество его элементов. Обозначается . Если , то множества А и В называются равномощными.

Определение. Если все элементы множества А являются также элементами множества В, то говорят, что множество А включается (содержится) в множестве В.

А Ì В

Определение. Если А Í В, то множество А называется подмножеством множества В (также говорят, что В покрывает А). Если при этом А ¹ В, то множество А называется собственным подмножеством множества В и обозначается А Ì В.

Замечание. Не следует считать равносильными отношения принадлежности и вхождения одного множества в другое . Можно привести следующий пример. Пусть А – множество всех студентов данной группы, а В – множество всех учебных групп данного института. Здесь 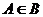, но , поскольку элементы этих множеств разнородны. Этот пример показывает также, что элементами множеств могут являться другие множества.

Парадокс Рассела. Задание множеств характеристическим предикатом может привести к противоречиям. Рассмотрим множество всех множеств, не содержащих себя в качестве элемента: . Если такое множество существует, то можно ответить на следующий вопрос: принадлежит ли оно само себе. С одной стороны, если , то . С другой стороны, если , то ! Это противоречие можно разрешить различными способами, в целом сводящимся к тому, что не является множеством.

Для трех множеств А, В, С справедливы следующие соотношения:

Связь между включением и равенством множеств устанавливается следующим соотношением:

Здесь знак Ù обозначает конъюнкцию (логическое “и”).

В заключение добавим, что Г. Кантор предложил использовать понятие “универсального множества” (универсум), как бы противоположного понятию пустого множества . По мысли Кантора, универсальное множество содержит все мыслимые множества, и при этом оно само содержится во множестве своих подмножеств в качестве элемента. В дальнейшем смысл и содержание понятия универсального множества будут раскрыты более подробно.

2. Операции над множествами и их свойства.

Определение. Объединением множеств А и В называется множество С, элементы которого принадлежат хотя бы одному из множеств А и В.

Обозначается С = А È В.

Геометрическое изображение множеств в виде области на плоскости называется диаграммой Эйлера – Вэйна.

Определение. Пересечением множеств А и В называется множество С, элементы которого принадлежат каждому из множеств А и В.

Обозначение С = А Ç В.

А С В

Для множеств А, В и С справедливы следующие свойства:

А Ç А = А È А = А; A È B = B È A; A Ç B = B Ç A;

(A Ç B) Ç C = A Ç (B Ç C); (A È B) È C = A È (B È C);

A È (B Ç C) = (A È B) Ç (A È C); A Ç (B È C) = (A Ç B) È (A Ç C);

A È (A Ç B) = A; A Ç (A È B) = A;

Æ = А; A Ç Æ = Æ;

Определение. Разностью множеств А и В называется множество, состоящее из элементов множества А, не принадлежащих множеству В.

Обозначается: С = А \ В.

А В

Определение. Симметрической разностью множеств А и В называется множество С, элементы которого принадлежат в точности одному из множеств А или В.

Обозначается: А D В.

А D В = (A \ B) È (B \ A)

A B

Определение. С_Е называется дополнением множества А относительно множества Е, если А Í Е и C_Е = Е \ A.

A E

Для множеств А, В и С справедливы следующие соотношения:

A \ B Í A; A \ A = Æ; A \ (A \ B) = A Ç B;

A D B = B D A; A D B = (A È B) \ (A Ç B);

A \ (B È C) = (A \ B) Ç (A \ C); A \ (B Ç C) = (A \ B) È (A \ C);

(A È B) \ C = (A \ C) È (B \ C); (A Ç B) \ C = (A \ C) Ç (B \ C);

A \ (B \ C) = (A \ B) È (A Ç C); (A \ B) \ C = A \ (B È C);

(A D B) D C = A D (B D C); A Ç (B D C) = (A Ç B) D (A Ç C);

A È C_EA = E; A Ç C_EA = Æ; C_EE = Æ; C_EÆ = E; C_EC_EA = A;

C_E(A È B) = C_EA Ç C_EB; C_E(A Ç B) = C_EA È C_EB;

Пример 2. Исходя из определения равенства множеств и операций над множествами, доказать тождество и проверить его с помощью диаграммы Эйлера - Вэйна.

Из записанных выше соотношений видно, что

Æ = A \ В

Что и требовалось доказать.

Для иллюстрации полученного результата построим диаграммы Эйлера – Вэйна:

А В А В

AÇB

Пример 3. Исходя из определения равенства множеств и операций над множествами, доказать тождество.

A \ (B È C) = (A \ B) Ç (A \ C)

Если некоторый элемент х Î А \ (В È С), то это означает, что этот элемент принадлежит множеству А, но не принадлежит множествам В и С.

Множество А \ В представляет собой множество элементов множества А, не принадлежащих множеству В.

Множество А \ С представляет собой множество элементов множества А, не принадлежащих множеству С.

Множество (A \ B) Ç (A \ C) представляет собой множество элементов, которые принадлежат множеству А, но не принадлежат ни множеству В, ни множеству С.

Таким образом, тождество можно считать доказанным.

3. Векторы и прямые произведения.

Вектором (кортежем) в линейной алгебре и дискретной математике называют упорядоченный набор элементов. Это не есть определение вектора, поскольку целесообразнее это понятие считать основным.

Элементы, определяющие вектор, называются координатами или компонентами. Координаты нумеруются слева направо, а их число называется длиной или размерностью вектора. В отличие от элементов множества, координаты вектора могут совпадать. Координаты вектора заключаются в круглые скобки, например 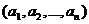. Иногда скобки или запятые опускаются. Часто векторы длины 2 называются упорядоченными парами, длины 3 – тройками и т. д.

Определение. Два вектора равны, если они имеют равную длину и их соответствующие координаты равны. Иначе говоря, векторы и равны, если и .

Определение. Прямым произведением множеств А и В (обозначение ) называется множество всех упорядоченных пар , таких, что . В частности, если А=В, то обе координаты принадлежат множеству А, такое произведение обозначается А². Аналогично, прямым произведением множеств называется множество всех векторов 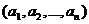длины п, таких, что .

Пример 4. Множество - это множество всех упорядоченных пар действительных чисел, геометрической интерпретацией которого служит декартова координатная плоскость.

Координатное представление точек плоскости было впервые предложено Р. Декартом и исторически является первым примером прямого произведения. Поэтому часто прямое произведение множеств называют декартовым произведением.

Пример 5. Даны множества и . Тогда есть множество обозначений клеток шахматной доски.

Вообще конечное множество, элементами которого являются какие-либо символы (буквы, цифры, знаки препинания, знаки операций и т. д.) называется алфавитом. Любые элементы множества в этом случае являются словами длины п в алфавите А. Например, десятичное целое число – это слово в алфавите цифр.

Определение. Проекцией вектора на некоторую ось называется его компонента (координата) с соответствующим порядковым номером (обозначается пр_i a). Например, проекция точки плоскости на 1-ю ось есть её абсцисса (первая координата).

Теорема 1.1. Мощность произведения конечных множеств равна произведению мощностей этих множеств: .

Следствие. .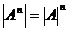

Эта простая теорема и её следствие впоследствии широко используются в комбинаторике.

Назад, в начало конспекта.

Лекция № 2. Соответствия и функции.

1. Соответствия.

Определение. Соответствием между множествами А и В называется некоторое подмножество G их декартова произведения: .

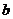Если , то говорят, что соответствует при соответствии . При этом множество всех таких называют областью определения соответствия , а множество соответствующих значений 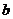называются областью значений соответствия .

В принятых обозначениях, каждый элемент , соответствующий данному элементу называется образом при соответствии , наоборот, элемент называется прообразом элемента при данном соответствии.

Соответствие называется полностью определённым, если , то есть каждый элемент множества имеет хотя бы один образ во множестве ; в противном случае соответствие называется частичным.

Соответствие называется сюръективным, если , то есть если каждому элементу множества соответствует хотя бы один прообраз во множестве .

Соответствие называется функциональным (однозначным), если любому элементу множества соответствует единственный элемент множества .

Соответствие называется инъективным, если оно является функциональным, и при этом каждый элемент множества имеет не более одного прообраза.

Соответствие называется взаимнооднозначным (биективным), если любому элементу множества соответствует единственный элемент множества , и наоборот. Можно сказать также, что соответствие является взаимнооднозначным, если оно является полностью определённым, сюръективным, функциональным, и при этом каждый элемент множества имеет единственный прообраз.

Пример 1.

а) Англо-русский словарь устанавливает соответствие между множествами слов русского и английского языка. Оно не является функциональным, так как почти каждому русскому слову соответствует несколько английских переводов; оно, также, не является, как правило, полностью определённым соответствием, так как всегда существуют английские слова, не включённые в данный словарь. Таким образом, это частичное соответствие.

б) Соответствие между аргументами функции 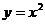и значениями этой функции является функциональным. Однако оно не является взаимнооднозначным, так как каждому значению функции соответствуют два прообраза и .

в) Соответствие между расположенными на шахматной доске фигурами и занимаемыми ими полями является взаимно однозначным.

г) Соответствие между телефонами города Вязьмы и их пятизначными номерами обладает, на первый взгляд, всеми свойствами взаимнооднозначного соответствия. Однако оно, например, не сюръективно, поскольку существуют пятизначные числа, не соответствующие никаким телефонам.

2. Взаимнооднозначные соответствия и мощности множеств.

Если между двумя конечными множествами А и В существует взаимнооднозначное соответствие, то эти множества равномощны. Этот очевидный факт позволяет, во-первых, установить равенство мощности этих множеств, не вычисляя их. Во-вторых, часто можно вычислить мощность множества, установив его однозначное соответствие с множеством, мощность которого известна, либо легко вычисляется.

Теорема 2.1. Если мощность конечного множества А равна , то число всех подмножеств А равно 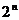, то есть .

Множество всех подмножеств множества М называется булеаном и обозначается . Для конечных множеств выполняется: .

Определение. Множества А и В называются равномощными, если между их элементами можно установить взаимнооднозначное соответствие.

Заметим, что для конечных множеств это утверждение легко доказать. Для бесконечных множеств оно определят само понятие равномощности.

Определение. Множество А называется счётным, если оно равномощно множеству натуральных чисел : .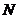

Очень упрощённо можно сказать, что данное бесконечное множество является счётным, если для его элементов можно установить нумерацию с помощью натуральных чисел.

Без доказательства примем ряд важных фактов:

1. Любое бесконечное подмножество множества натуральных чисел является счётным.

2. Множество является счётным.

3. Множество рациональных чисел является счётным (является следствием из предыдущего утверждения).

4. Объединение конечного числа счётных множеств является счётным.

5. Объединение счётного числа конечных множеств является счётным.

6. Объединение счётного числа счётных множеств является счётным.

Все эти утверждения, как можно видеть, позволяют достаточно успешно устанавливать факт, что данное множество является счётным. Однако сейчас будет показано, что не всякое бесконечное множества является счётным; существует множества большей мощности.

Теорема 2.2 (теорема Кантора). Множество всех действительных чисел из отрезка не является счётным.

Доказательство. Допустим, что множество является счётным и существует его нумерация. Поскольку любое действительное число можно представить в виде бесконечной десятичной дроби (периодической или непериодической), то проделаем это с числами данного множества. Расположим их в порядке этой нумерации:

Теперь рассмотрим любую бесконечную десятичную дробь вида , организованную таким образом, что и так далее. Очевидно, что данная дробь не входит в рассматриваемую последовательность, поскольку от первого числа она отличается первой цифрой после запятой, от второго – второй цифрой и так далее. Следовательно, мы получили число из данного интервала, которое не пронумеровано и, таким образом, множество 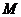не является счётным. Его мощность называется континуум, а множества такой мощности называются континуальными. Приведённый метод доказательства называется диагональным методом Кантора.

Следствие 1. Множество действительных чисел континуально.

Следствие 2. Множество всех подмножеств счётного множества континуально.

Как показывается в теории множеств (с помощью метода, аналогичного приведённому выше), для множества любой мощности множество всех его подмножеств (булеан) имеет более высокую мощность. Поэтому не существует множества максимальной мощности. Например, множество-универсум , описанное Кантором должно содержать все мыслимые множества, однако оно само содержится в множестве своих подмножеств в качестве элемента (парадокс Кантора). Получается, что множество не является множеством максимальной мощности.

3. Отображения и функции.

Функцией называется любое функциональное соответствие между двумя множествами. Если функция устанавливает соответствие между множествами А и В, то говорят, что функция имеет вид (обозначение ). Каждому элементу из своей области определения функция ставит в соответствие единственный элемент 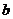из области значений. Это записывается в традиционной форме . Элемент называется аргументом функции, элемент 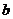- её значением.

Полностью определённая функция называется отображением А в В; образ множества А при отображении обозначается . Если при этом , то есть соответствие сюръективно, говорят, что имеет отображение А на В.

Если состоит из единственного элемента, то называется функцией-константой.

Отображение типа называется преобразованием множества А.

Пример 2.

а) Функция является отображением множества натуральных чисел в себя (инъективная функция). Эта же функция при всех 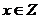является отображением множества целых чисел в множество рациональных чисел.

б) Функция является отображением множества целых чисел (кроме числа 0) на множество натуральных чисел. Причём в данном случае соответствие не является взаимно однозначным.

в) Функция является взаимнооднозначным отображением множества действительных чисел на себя.

г) Функция не полностью определена, если её тип 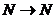, но полностью определена, если её тип 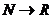или .

Определение. Функция типа называется местной функцией. В этом случае принято считать, что функция имеет аргументов: , где .

Например, сложение, умножение, вычитание и деление являются двухместными функциями на , то есть функциями типа .

Определение. Пусть дано соответствие . Если соответствие 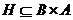таково, что тогда и только тогда, когда , то соответствие называют обратным к и обозначают .

Определение. Если соответствие, обратное к функции является функциональным, то оно называется функцией, обратной к .

Очевидно, что в обратном соответствии образы и прообразы меняются местами, поэтому для существования обратной функции требуется, чтобы каждый элемент из области значения имел бы единственный прообраз. Это означает, что для функции обратная функция существует тогда и только тогда, когда является биективным соответствием между своей областью определения и областью значений.

Пример 3. Функция имеет тип 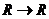. Отрезок она взаимно однозначно отображает на отрезок . Поэтому для неё на отрезке существует обратная функция. Как известно, это .

Определение. Пусть даны функции и 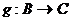. Функция называется композицией функций и 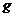(обозначается ), если имеет место равенство: , где .

Композиция функций и 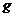представляет собой последовательное применение этих функций; 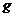применяется к результату .Часто говорят, что функция 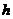получена подстановкой в .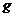

Для многоместных функций возможны различные варианты подстановок в 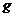, дающие функции различных типов. Особый интерес представляет случай, когда задано множество функций типа: 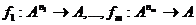. В этом случае возможны, во-первых, любые подстановки функций друг в друга, а во-вторых, любые переименования аргументов. Функция, полученная из данных функций некоторой подстановкой их друг в друга и переименованием аргументов, называется их суперпозицией.

Например, в математическом анализе вводится понятие элементарной функции, являющейся суперпозицией фиксированного (не зависящего от значения аргумента) числа арифметических операций, а также элементарных функций ( и т. п.).

А.Н. Колмогоровым и В.И. Арнольдом доказано, что всякая непрерывная функция переменных представима в виде суперпозиции непрерывных функций двух переменных.

Замечание. Понятие функции широко используется в математическом анализе, более того, является в нём базовым понятием. В целом, подход к пониманию термина “функция” в матанализе несколько уже, чем в дискретной математике. Как правило, в нём рассматриваются так называемые вычислимые функции. Функция называется вычислимой, если задана процедура, позволяющая по любому заданному значению аргумента найти значение функции.

Назад, в начало конспекта.

Лекция № 3. Отношения и их свойства.

1. Основные понятия и определения.

Определение. Подмножество называется местным ( мерным) отношением на множестве А. Говорят, что элементы находятся в отношении , если .

Одноместное (одномерное) отношение – это просто некоторое подмножество А. Такие отношения называют признаками. Говорят, что обладает признаком , если и . Свойства одноместных отношений – это свойства подмножеств А, поэтому для случая термин “отношения” употребляется редко.

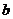Наиболее часто встречающимися и хорошо изученными являются двухместные или бинарные отношения. Если и находятся в отношении , это обычно записывается в виде .

Пример 1. Бинарные отношения на множестве .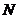

а) Отношение “ ” выполняется для пар и не выполняется для пары .

б) Отношение “иметь общий делитель, не равный единице” выполняется для пар и не выполняется для пар .

в) Отношение “быть делителем” выполняется для пар и не выполняется для пар .

Пример 2. Бинарные отношения на множестве точек координатной плоскости.

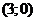а) Отношение “быть равноудалёнными от начала координат” выполнятся для пар точек и , но не выполнятся для пары точек и .

б) Отношение “принадлежать окружности, центр которой находится в начале координат”, выполняется для первой пары точек из предыдущего примера и не выполняется для второй пары.

в) Отношение “быть удалёнными на разное расстояние от начала координат” выполняется для всех точек, для которых не выполняется отношение, описанное в пункте “б”.

Пусть дано отношение на множестве А. Для любого подмножества определяется отношение , называемое сужением на , которое получается из отношения удалением всех пар, содержащих элементы, не принадлежащие . Иначе говоря, .

Строго говоря, само отношение и его сужение - это разные отношения, с разными областями определения. Однако, по умолчанию, если не возникает явных разночтений, эта разница не учитывается. Например, вполне можно говорить об отношении “быть делителем”, не уточняя, задано оно на множестве 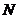или на каком-нибудь его подмножестве.

Для задания бинарных отношений можно использовать любые способы задания множеств (например, список пар, для которых данное отношение выполняется). Отношения на конечных множествах обычно задаются списком или матрицей. Матрица бинарного отношения на конечном множестве - это квадратная матрица порядка , в которой каждый элемент определяется следующим образом:

Пример 3. Для конечного множества матрицы отношений из примера 1 (а – в) приведены в следующих таблицах.

а)

	1	2	3	4	5	6
1	1	1	1	1	1	1
2	0	1	1	1	1	1
3	0	0	1	1	1	1
4	0	0	0	1	1	1
5	0	0	0	0	1	1
6	0	0	0	0	0	1

б)

	1	2	3	4	5	6
1	0	0	0	0	0	0
2	0	1	0	1	0	1
3	0	0	1	0	0	1
4	0	1	0	1	0	1
5	0	0	0	0	1	0
6	0	1	1	1	0	1

в)

	1	2	3	4	5	6
1	1	1	1	1	1	1
2	0	1	0	1	0	1
3	0	0	1	0	0	1
4	0	0	0	1	0	0
5	0	0	0	0	1	0
6	0	0	0	0	0	1

Поскольку отношения на множестве А задаются подмножествами А², для отношений можно определить те же операции, что и для множеств. Например, отношение “ ” является объединением отношений “<” и “=”.

Определение. Отношение называется обратным к отношению , если тогда и только тогда, когда .

Непосредственно из определения следует, что . Например, для отношения “ ” обратным является отношение “ ”.

2. Свойства отношений.

Определение. Отношение называется рефлексивным, если для любого элемента имеет место .

Главная диагональ матрицы рефлексивного отношения содержит только единицы.

Определение. Отношение называется антирефлексивным, если ни для какого элемента не выполняется .

Главная диагональ матрицы рефлексивного отношения содержит только нули.

Например, отношения “ ” и “иметь общий делитель” являются рефлексивными. Отношения “ ” и “иметь сына” являются антирефлексивными. Отношение “быть симметричным относительно оси абсцисс” не является ни рефлексивным, ни антирефлексивным: точка плоскости симметрична сама себе, если лежит на этой оси, и не симметрична себе, если не лежит на ней.

Определение. Отношение называется симметричным, если для любой пары из отношения следует . Иными словами, отношение является симметричным тогда и только тогда, когда для любой пары оно выполняется в обе стороны (или вовсе не выполняется).

Матрица симметричного отношения симметрична относительно главной диагонали: для любых .

Определение. Отношение называется антисимметричным, если из отношений и следует, что .

Отношение “быть симметричным относительно оси абсцисс” является симметричным: если первая точка симметрична второй относительно этой оси, то и вторая точка симметрична первой. Отношение “ ” является антисимметричным. Действительно, если и , это означает, что .

Нетрудно убедиться в том, что отношение симметрично тогда и только тогда, когда .

Определение. Отношение называется транзитивным, если для любых из отношений и следует .

Отношения “быть равным”, “жить в одном городе”, “быть параллельным” являются транзитивными. Отношения “пересекаться”, “быть сыном” не являются транзитивными.

Замечание. В отличие от отношений рефлексивности и симметричности, для отношения транзитивности не формулируется противоположного понятия (антитранзитивности).

Определение. Транзитивным замыканием отношения называется отношение, определяемое следующим образом: если в множестве 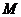существует цепочка из элементов , в которой между каждыми двумя соседними элементами выполняется отношение (, то говорят, что существует транзитивное замыкание .

Замечание. Замыкание является весьма общим математическим понятием. Упрощённо говоря, замкнутость означает, что многократное повторение допустимых шагов не выводит за определённые границы. Например, множество натуральных чисел замкнуто относительно операции сложения, однако открыто (то есть незамкнуто) относительно операции деления.

Если отношение транзитивно, то, очевидно, 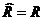(и наоборот). Например, отношение “быть делителем” транзитивно для любой цепочки элементов и само является транзитивным замыканием этого отношения.

Если отношение не транзитивно, то .

Например, транзитивным замыканием отношения “быть сыном” является отношение “быть прямым потомком”, включающее в себя понятия “быть сыном”, “быть внуком”, “быть правнуком” и так далее.

Назад, в начало конспекта.

Лекция № 4. Основные виды отношений.

Из содержания предыдущей лекции и рассмотренных в ней примеров видно, что понятие “отношение” следует понимать весьма широко. В данной лекции мы попытаемся ввести определённую классификацию отношений и рассмотреть наиболее значительные с точки зрения математики виды отношений – а именно отношения эквивалентности и порядка.

Отношения эквивалентности.

Определение. Отношение называется отношением эквивалентности (или просто эквивалентностью), если оно рефлексивно, симметрично и транзитивно.

Пример 1.

а) Отношение равенства (часто обозначается ) на любом множестве является отношением эквивалентности. Равенство – это минимальное отношение эквивалентности в том смысле, что при удалении любой пары из этого отношения (то есть любой единицы на главной диагонали матрицы ) оно перестаёт быть рефлексивным и, следовательно, уже не является эквивалентностью.

б) Утверждения вида или , состоящие из формул, соединённых знаком равенства, задают бинарное отношение на множестве формул, описывающих суперпозиции элементарных функций. Это отношение обычно называется отношением равносильности и определяется следующим образом: две формулы равносильны, если они задают одну и ту же функцию. Равносильность в данном случае, хотя и обозначена знаком “=”, означает не то же самое, что отношение равенства, так как оно может выполняться для различных формул. Впрочем, можно считать, что знак равенства в таких отношениях относится не к самим формулам, а к функциям, которые ими описываются. Для формул же отношение равенства – это совпадение формул по написанию. Оно называется графическим равенством. Кстати, чтобы в подобных ситуациях избежать разночтений, часто для обозначения отношения равносильности используют знак “ ”.

в) Рассмотрим множество треугольников на координатной плоскости, считая, что треугольник задан, если даны координаты его вершин. Два треугольника будем считать равными (конгруэнтными), если при наложении они совпадают, то есть, переведены друг в друга с помощью некоторого перемещения. Равенство является отношением эквивалентности на множестве треугольников.

г) Отношение “иметь один и тот же остаток отделения на натуральное число 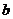” на множестве натуральных чисел является отношением эквивалентности.

е) Отношение “быть делителем” не является на множестве 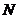отношением эквивалентности. Оно обладает свойствами рефлексивности и транзитивности, но является антисимметричным (см. ниже).

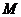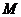Пусть на множестве задано отношение эквивалентности . Осуществим следующее построение. Выберем элемент и образуем класс (подмножество ), состоящий из элемента и всех элементов, эквивалентных ему в рамках данного отношения. Затем выберем элемент и образуем класс 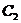, состоящий из и эквивалентных ему элементов. Продолжая эти действия, получим систему классов 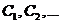(возможно, бесконечную) такую, что любой элемент из множества