ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Рассматриваем движение ТТ под действием системы сил 
в инерциальном пространстве Оxyz.
Дифференциальные уравнения поступательного движения твердого тела
За обобщенные координаты поступательно движущегося ТТ примем координаты (xc, yc, zc) его центра масс С. Из теоремы о движении центра масс МСМТ вдоль координатных осей
, 
, 
.
Дифференциальные уравнения вращательного движения твердого тела вокруг неподвижной оси
За обобщенную координату тела примем угол поворота φ. Из теоремы об изменении кинетического момента относительно оси вращения
.
Дифференциальные уравнения плоского движения твердого тела
За обобщенные координаты тела примем координаты xc, yc его центра масс и угол поворота φ тела около оси z C, перпендикулярной направляющей плоскости. Из теоремы о движении центра масс и теоремы об изменении кинетического момента относительно оси
, , 
.
Интегрируя ДУ при известных силах , действующих на ТТ, и начальных условиях движения, можно найти уравнения плоского движения
, 
, 
.
ПРИНЦИП ДАЛАМБЕРА ДЛЯ МСМТ И ТТ
Рассматривается движение МСМТ {M k } n с массами { mk } n с радиус-векторами 
под действием внешних 
и внутренних 
сил в инерциальном пространстве Oxyz.
По аналогии с МТ принцип Даламбера для МСМТ:
Силы внешние , внутренние , под действием которых движется система, и силы инерции точек системы 
образуют уравновешенную систему сил
.
Принцип Даламбера для ТТ:
Твердое тело представляется как геометрически неизменяемая МС материальных частиц массой d m. Так как в твердом теле внутренние силы уравновешиваются (
), то принцип Даламбера:
в каждый момент времени внешние силы , приложенные к ТТ, и силы инерции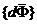 
частиц тела образуют уравновешенную систему сил
.
- сила инерции материальной частицы массы dm, движущейся в пространстве Oxyz с ускорением 
.
Образована уравновешенная система сил, для которой используются уравнения статики.
Силы инерции
При любом движении твердого тела главный вектор сил инерции частиц равен произведению массы тела на ускорение его центра масс
.
Главный момент сил инерции зависит от выбора центра и вида движения тела.
Приведение сил инерции к центру А
Силы инерции 
заменяются результирующей силой 
, равной главному вектору этих сил, и результирующей парой, момент 
которой равен главному моменту сил относительно этого центра
, 
, 
.
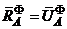Поступательное движение: приведение к центру масс,
, 
, 
.
Вращательное движение: приведение к неподвижному центру на оси вращения,
, 
, 
.
Если ось вращения является главной центральной осью инерции,
, 
, 
, 
, 
.
Плоское движение: приведение у центру масс в плоскости материальной симметрии,
, , 
.
