При векторном способе задания движения:
, 
, 
.
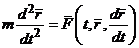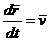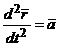В координатной форме:
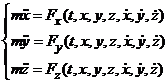
В естественной форме:
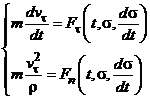
Интегрируя дважды по времени, получаем уравнения движения точки в координатной форме. Постоянные интегрирования определяют с использованием начальных (граничных) условий:
При t = 0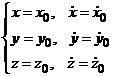 
Задача Д1
Дифференциальные уравнения движения несвободной материальной точки
В этом случае используется принцип освобождаемости от связей: движение несвободной материальной точки не изменится, если ее сделать свободной и заменить связи их реакциями.
, 
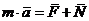- реакция связи.
Задача Д2
СИЛА ИНЕРЦИИ МТ. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МТ
Рассматривается движение МТ М под действием силы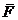 
, приложенной к ней со стороны тела А - ускоряющего тела.
Если ускоряющих тел несколько, то 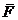- равнодействующая. Эта сила определяется уравнением
.
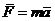В соответствии с законом о равенстве действия и противодействия точка М действует на тело А с силой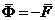 
. Поэтому
- сила инерции МТ.
Проекции силы инерции на декартовы оси и оси Эйлера
, 
, 
, 
, 
.
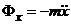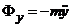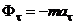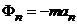Пусть несвободная МТ М движется в инерциальном пространстве Oxyz.
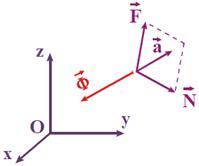
Основное уравнение динамики для нее имеет вид
.
Здесь 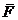и - равнодействующие заданных сил и реакций связей. Тогда
.
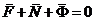Принцип Даламбера для МТ: Заданные силы и реакции связей, под действием которых движется точка, и сила инерции точки образуют уравновешенную систему сил
.
ДИНАМИЧЕСКИЕ МЕРЫ МАТЕРИАЛЬНЫХ ОБЪЕКТОВ
Динамическими мерами являются:
- масса;
- моменты инерции;
- количество движения;
- момент количества движения (кинетический момент);
- кинетическая энергия.
Масса, момент инерции – меры инертности МО, остальные – динамические меры механического движения МО.
Масса, центр масс МСМТ
Пусть в пространстве Oxyz рассматривается движение МСМТ {M k } n с массами { mk } n, положение которых определяется радиус-векторами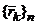 
.
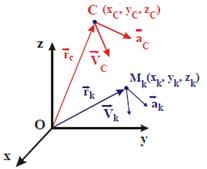
Массой МСМТ называется величина, равная сумме масс точек системы
.
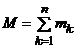Центром масс (ЦМ) МСМТ называется точка С пространства Oxyz, радиус-вектор которой в каждый момент времени равен
.
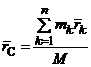Координаты (х С, у С, z С) ЦМ МСМТ:
, 
, 
.
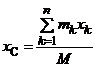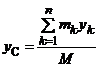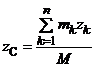Моменты инерции МСМТ и ТТ
Момент инерции МСМТ относительно оси (осевой момент инерции) – сумма произведений масс всех точек системы на квадраты их расстояний до этой оси:
,
,
.
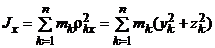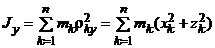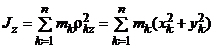Момент инерции МСМТ относительно центра О (полярный моментом инерции) - сумма произведений масс всех точек системы на квадраты их расстояний до центра:
.
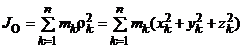Осевые и полярный моменты инерции характеризуют разброс точек МС относительно оси и центра.
Центробежный момент инерции МСМТ - сумма произведений масс всех точек системы на координаты этих точек вдоль двух осей:
,
,
.
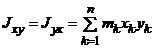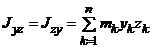Центробежные моменты инерции характеризуют асимметрию распределения МТ относительно координатных плоскостей.
Радиусом инерции МСМТ (ТТ) относительно оси l ~ (х, у, z) называется
.
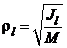Зная радиус инерции, момент инерции МСМТ (ТТ)
.
