При построении гистограммы была выдвинута гипотеза о законе распределения генеральной совокупности. Назовем этот закон распределения теоретическим. Проверим его согласие с распределением выборки.
Сущность проверки статистической гипотезы заключается в том, чтобы установить, согласуются или нет данные наблюдения и выдвинутая гипотеза, можно ли расхождения между гипотезой и результатом выборочных наблюдений отнести за счет случайной погрешности, обусловленной механизмом случайного отбора. При этом критерии в задачах проверки гипотез о параметрах распределения называют критериями значимости, а в задачах проверки гипотез о законах распределения – критериями согласия.
Процесс проверки статистической гипотезы сводится к следующему:
- выдвигается основная гипотеза 
и множество альтернативных гипотез 
;
- выбирается критерий, представляющий собой некоторую меру близости между гипотетическим и эмпирическим распределениями или между гипотетической и эмпирической характеристиками распределения;
- критерий выбирается так, чтобы его распределение было известно;
- назначается уровень значимости 
;
- производится опыт и по данным опыта (выборочным наблюдениям) вычисля-
ется значение критерия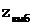 
;
- если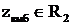 
, то гипотеза отвергается, если 
, то гипотеза не отвергается на уровне значимости .
Из большого числа различных критериев чаще других используется критерий согласия 
, предложенный К. Пирсоном. В этом критерии в качестве меры расхождения теоретического и статистического распределений выбирается величина , определяемая равенством
, (4)
где n – объем выборки;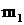 
– число интервалов, на которые разбита выборка;
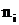–число элементов выборки, попавших в 
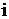-й интервал; 
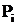– теоретическая вероятность попадания значений случайной величины в 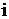-й интервал.
Вероятность 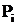определяется в согласии с теоретическим законом распределения
, (5)
или 
, (6)
где 
- границы 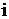–го интервала.
Примеры
Пусть выдвинуты гипотезы о распределении генеральной совокупности:
1) по показательному закону 
где 
- оценка параметра показательного закона распределения по выборке; 
. Здесь 
- оценка математического ожидания;
2) по нормальному закону 
,
где - оценка математического ожидания, 
- оценка дисперсии по выборке. 
- оценка среднего квадратичного; 
- функция Лапласа (табл. А1);
3) по закону Релея 
,
где 
- оценка параметра закона Релея по выборке: 
;
4) по равномерному закону 
,
где 
- оценки крайних значений выборки, которые находятся из системы 
.
Случайная величина , независимо от вида закона распределения генеральной совокупности, при достаточно больших 
имеет распределение с числом степеней свободы 
, где 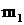- число интервалов, r – число параметров распределения, определенных по выборке.
Задаваясь уровнем значимости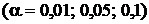 
, по таблице А2 определим критическое значение 
, такое, что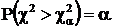 
. При больших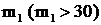 
распределено асимптотически нормально и можно пользоваться таблицами нормального закона. Если 
, то выдвинутая гипотеза о виде закона распределения генеральной совокупности не отвергается на уровне значимости (гипотеза не противоречит опытным данным), если же 
, то гипотеза отвергается на уровне значимости .
Замечание. Критерий Пирсона обладает большей мощностью, если интервалы содержат примерно равное число элементов, при этом длины интервалов не обязательно должны быть равными. Поэтому при использовании критерия Пирсона нужно произвести новое разбиение данной выборки на интервалы, содержащие примерно равное число элементов.
Замечание. Все расчеты вести с тем количеством знаков, с каким даны значе-
ния случайной величины (можно добавить один дополнительный знак).
