ЛАБОРАТОРНАЯ РАБОТА №2
Исследование частотных характеристик элементарных
Динамических звеньев
Краткие теоретические сведения
Будем рассматривать следующую систему
Рис.2.1.
Пусть в общем случае линейная система описывается дифференциальным уравнением n-го порядка
... 
... 
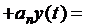
, (2.1)
где 
и 
соответственно входной и выходной сигналы системы. Преобразуем левую и правую части этого уравнения по Лапласу. В результате получим следующее алгебраическое уравнение
, (2.2)
где 
- оператор дифференцирования.
Передаточной функцией системы называется отношение выходного сигнала к входному, преобразованных по Лапласу при нулевых начальных условиях. Тогда передаточная функция рассматриваемой системы равна
. (2.3)
Частотные характеристики системы, в том числе элементарных динамических звеньев, могут быть получены при рассмотрении реакции системы на гармонические воздействия разной частоты. При прохождении через линейную систему гармонического сигнала разной частоты у выходного сигнала в общем случае изменяются только амплитуда и фаза, частота остается неизменной. К частотным характеристикам относятся:
- амплитудно - фазовая частотная характеристика (АФЧХ),
- амплитудная частотная характеристика (АЧХ),
- фазовая частотная характеристика (ФЧХ),
- логарифмическая амплитудная частотная характеристика (ЛАЧХ),
- логарифмическая фазовая частотная характеристика (ЛФЧХ).
Рассмотрим частотную передаточную функцию, которая получается из передаточной функции (2.3) путем замены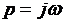 
, где 
является частотой
. (2.4)
Функцию 
можно записать в следующем виде
, (2.5)
где
(2.6)
На комплексной плоскости представляет собой вектор, при изменении частоты 
от 
до + 
конец вектора описывает кривую, называемую амплитудно - фазовой частотной характеристикой (АФЧХ). Например АФЧХ может иметь следующий вид
Рис.2.2.
Длина вектора равна 
. График 
является амплитудной частотной характеристикой (АЧХ)
Рис.2.3.
На этой характеристике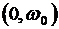 
- полоса пропускания системы, 
- резонансная частота, а 
- частота среза.
Аргумент 
, представляющий собой угол между вектором и действительной положительной полуосью называют фазовой частотной характеристикой (ФЧХ). Кроме того, в соответствии с (2.5) график действительной части 
называется вещественной частотной характеристикой, а график мнимой части 
- мнимой частотной характеристикой.
Наряду с перечисленными частотными характеристиками самое широкое применение находят логарифмические частотные характеристики (ЛЧХ), а именно логарифмические амплитудно-частотные и фазо-частотные характеристики - соответственно ЛАЧХ и ЛФЧХ. Для ЛАЧХ по оси ординат откладывают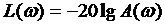 
. Единицей измерения 
является децибел. Для ЛФЧХ по оси ординат откладывается значение угла в градусах. По оси абсцисс откладывают частоту в логарифмическом масштабе, причем на отметке, соответствующей значению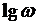 
, записывается само значение частоты 
Ось ординат проходит не через точку 
, так как в этом случае 
, а через произвольную точку обычно малой частоты.
Рис. 2.4.
На рисунке 2.4 изображена так называемая реальная ЛАЧХ. На практике обычно ограничиваются построением асимптотических ЛАЧХ, представляющих собой ломаные линии (на рисунке пунктирная линия). Частоты при которых пересекаются асимптоты называются сопрягающими, они связаны с постоянными времени системы соотношением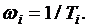 
Получим в MATHCAD 7 частотные характеристики, рассмотренных в лабораторной работе №1 элементарных динамических звеньев. Частотные передаточные функции этих звеньев имеют следующий вид:
- безынерционное звено
;
- апериодическое звено
;
- колебательное звено
;
- интегрирующее звено
;
- дифференцирующее звено
.
Рассмотрим также частотные характеристики форсирующих звеньев, имеющих следующие частотные передаточные функции:
- первого порядка
;
- второго порядка
.
Кроме того исследуем частотные характеристики двух неустойчивых неминимально-фазовых звеньев с частотными передаточными функциями
,
.
Программа в MATHCAD 7 получения частотных характеристик апериодического звена имеет следующий вид.
Задаем диапазон изменения
Записываем частотную передаточную функцию
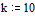
Формируем вещественную и мнимую частотные функции
Формируем АЧХ и ФЧХ звена
Выводим графики частотных характеристик
АФЧХ
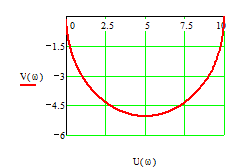
Рис.2.5.
АЧХ ФЧХ
Рис.2.6.
ЛЧХ
Рис.2.7.
Приведем, полученные в MATHCAD 7 частотные характеристики звеньев:
- безынерционного при k=10
АФЧХ
АЧХ ФЧХ
ЛЧХ
Рис.2.8.
- колебательного при k=10, T=0.1 и x=0,5.
АФЧХ
АЧХ ФЧХ
ЛЧХ
Рис.2.9.
- интегрирующего звена при k=10
АФЧХ
АЧХ ФЧХ
ЛЧХ
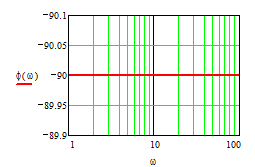
Рис.2.10.
- дифференцирующего звена при k=10
АФЧХ
АЧХ ФЧХ
ЛЧХ
Рис.2.11.
ЛАЧХ и ЛФЧХ форсирующего звена первого порядка при k=1 и T=0,1 имеют вид
Рис.2.12.
Необходимо отметить, что в отличие от апериодического звена наклон ЛАЧХ после точки сопряжения составляет +20 дБ/дек, а фазовый сдвиг стремиться к +90 градусов.
У форсирующего звена 2-го порядка (Рис.2.13) наклон ЛАЧХ после точки сопряжения составляет уже +40 дБ/дек, а фазовый сдвиг стремиться к +180 градусов.
Рис.1.13.
Так как сдвиг фазы у рассмотренных звеньев стремиться у одного к +90 градусов, а у второго к +180 градусов, то поэтому эти звенья и относится к форсирующему типу.
Приведем, полученные в MATHCAD 7 ЛЧХ неустойчивого апериодического звена
Рис.2.12.
и неустойчивого колебательного звена
Рис.2.13.
Из анализа ЛАХ неустойчивых звеньев следует, что ЛАЧХ соответствующих устойчивых и неустойчивых звеньев совпадают. Фазовые сдвиги у неустойчивых звеньев по абсолютному значению выше, по сравнению с устойчивыми звеньями. Поэтому неустойчивые звенья и получили название неминимально-фазовых в отличие от устойчивых - минимально-фазовых звеньев.
2) Задание на лабораторную работу
а) Для апериодического звена получить частотные характеристики (АФЧХ, АЧХ, ФЧХ, ЛАЧХ и ЛФЧХ) при следующих исходных данных
Таблица 2.1
| k | 0.5 | 1 | 2 |
| T | 0.1 | 0.2 | 0.3 |
Оценить влияние на эти характеристики параметров звена k и T.
б) Для колебательного звена при исходных данных, приведенных в таблицах 2.2 и 2.3. получить частотные характеристики (АФЧХ, АЧХ, ФЧХ, ЛАЧХ и ЛФЧХ).
Таблица 2.2
x 
| 0.5 | 0.5 | 0.5 |
| k | 0.5 | 1 | 2 |
| T | 1 | 0.2 | 0.3 |
Таблица 2.3
| x | 0 | 0.1 | 0.5 | 0.8 | 1 | 2 |
| k | 1 | 1 | 1 | 1 | 1 | 1 |
| T | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
Оценить влияние на эти характеристики параметров звена k,T и x.
в) Для интегрирующего звена при k=1, 10 и 100 получить частотные характеристики (АФЧХ, АЧХ, ФЧХ, ЛАЧХ и ЛФЧХ). Оценить влияние коэффициента передачи на вид характеристик.
г) Для дифференцирующего звена при k=1, 10 и 100 получить частотные характеристики (АФЧХ, АЧХ, ФЧХ, ЛАЧХ и ЛФЧХ). Оценить влияние коэффициента передачи на вид характеристик.
д) Для неустойчивого (неминимально-фазового) колебательного звена при k=1, T=0.01 и x=0,1 получить ЛАЧХ и ЛФЧХ. Сравнить их с аналогичными характеристиками устойчивого колебательного звена.
3) Отчет по лабораторной работе
Отчет должен содержать:
- cхему моделирования;
- частотные передаточные функции звеньев;
- аналитический вид частотных характеристик;
- программы моделирования;
- полученные частотные характеристики;
- найденные значения частоты среза, частоты пропускания и резонансной частоты (если есть);
- выводы.
В выводах должна быть дана оценка влияния коэффициентов исследуемых звеньев на вид частотных характеристик.
4) Вопросы для самопроверки
1. Какие существуют частотные характеристики?
2. Какие параметры изменяются у синусоидального сигнала при его прохождении через линейную систему?
3. Что такое АФЧХ, как она находится, какие частотные характеристики по ней могут быть определены?
4. Как определяются логарифмические частотные характеристики?
5. Что такое частота сопряжения и как она определяется?
6. Как определить полосу пропускания системы?
7. Как влияет на вид ЛАЧХ колебательного звена изменение коэффициента демпфирования?
8. Какие звенья относятся к звеньям форсирующего типа и почему?
9. Какие звенья называются неминимально-фазовыми?
