Систему автоматического управления можно представить состоящей из ряда элементарных динамических звеньев. Под элементарными динамическими звеньями понимаются устройства, которые могут иметь различный физический вид и конструкцию, однако описываться они должны дифференциальными уравнениями не выше второго порядка. Поэтому и классифицируются элементарные динамические звенья по виду их уравнения.
Представим звено в следующем виде
Рис.1.1.
Здесь x(t) и y(t) соответственно входной и выходной сигналы.
Простейшим из звеньев является безынерционное звено, которое описывается дифференциальным уравнением нулевого порядка - алгебраическим уравнением
, (1.1)
где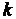 
- безразмерный коэффициент передачи (усиления) звена. К безынерционным звеньям относятся различные датчики сигналов, электронные усилители, механические редукторы и т. п. Необходимо отметить, что уравнение (1.1) не является реальным, точно отражающим характер процессов, протекающих в той или иной системе. Оно является некоторой идеальной моделью, не учитывающей инерционность датчиков или усилителей, пренебрегающей упругими свойствами и люфтами в редукторах и т. п.
Апериодическое звено (звено первого порядка) имеет следующее дифференциальное уравнение
, (1.2)
где 
- постоянная времени, 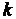- коэффициент передачи (усиления) звена. Постоянная времени имеет размерность секунд.
Апериодическим звеном можно описать поведение двигателя внутреннего сгорания или электродвигателя, причем если входной величиной является расход топлива (управляющее напряжение), то выходной величиной будет являться частота вращения вала двигателя. Это же звено является математической моделью электрической печи, электрического генератора постоянного тока и т. п.
Дифференциальное уравнение второго порядка в зависимости от величины коэффициентов имеют три звена
, (1.3)
где - постоянная времени, 
- безразмерный коэффициент демпфирования, 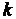- коэффициент передачи (усиления) звена.
Если коэффициент демпфирования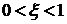 
, то звено называется колебательным, если 
звено называется консервативным, если же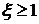 
- апериодическое звено второго порядка.
Колебательным звеном описываются двигатели постоянного тока при некоторых значениях параметров, движение летательного аппарата относительно какой либо оси, поведение гироскопической системы и т. п.
Консервативное звено является частным случаем колебательного и описывает режим возникновения в той или иной системе незатухающих колебаний.
Апериодическое звено второго порядка эквивалентно двум последовательно включенным апериодическим звеньям первого порядка.
Интегрирующее звено имеет следующее дифференциальное уравнение
, (1.4)
где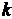 
- коэффициент передачи (усиления) звена. Примером интегрирующего звена является электродвигатель, выходной величиной которого является угол поворота вала, являющейся интегралом от угловой скорости. К интегрирующему звену можно отнести гидравлический демпфер, причем входной является сила, приложенная к поршню, а выходной величиной будет являться перемещение штока.
Для дифференцирующего звена справедливо уравнение
. (1.5)
В технике не существует реальных объектов, которые бы описывались таким уравнением. Оно соответствует идеальному дифференцирующему звену. В качестве примера такого звена можно назвать тахогенератор, входной величиной которого является угол поворота ротора, а выходной - напряжение на якоре.
Для исследования систем используют и другие типы звеньев, причем на некоторых из них мы остановимся ниже.
В ТАУ рассматриваются два типа временных динамических характеристик переходные и импульсные. Переходной функцией 
звена или системы называется ее реакция на единичное ступенчатое воздействие 
при нулевых начальных условиях. Единичное степенчатое воздействие представим в следующем виде
(1.6)
Рис.1.2.
Функция h(t) является переходной функцией, а ее график - переходной характеристикой.
Импульсной переходной или весовой функцией (функцией веса) 
звена (системы) называется ее реакция на единичное импульсное воздействие 
при нулевых начальных условиях. График этой функции - импульсная переходная характеристика. Опишем единичное импульсное воздействие
(1.7)
Рис.1.3.
Необходимо отметить, что
(1.8)
В MATHCAD 7 ступенчатые воздействия моделируются с помощью кусочно-непрерывной функции if(a,b,c). Она используется для определения функции, которая ведет себя по разному слева и справа от точки разрыва 
. Точка разрыва определяется первым аргументом функции if(a,b,c), а два других аргумента 
и 
определяют поведение функции по обе стороны от точки разрыва. Тогда единичную ступенчатую функцию представим в виде
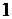(t) = if(t<0,0,1). (1.9)
Приведем программу моделирования единичного ступенчатого воздействия в MATCHAD 7 на отрезке времени от 0 до 1 сек. с шагом 0, 01 сек.
Рис.1.4.
Необходимо отметить, что принципиально невозможно осуществить моделирование бесконечно высокого и узкого импульса 
-функции. Импульсная функция в MATHCAD 7 моделируется путем нахождения разности двух ступенчатых функций. Запишем программу моделирования импульсного воздействия с амплитудой 
(t)=1000 на отрезке времени от 0 до 1 сек. с шагом 0, 001 сек.
Программа моделирования импульсного воздействия
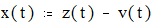
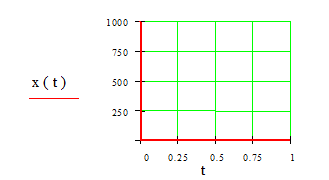
Рис.1.5.
Схема моделирования переходных характеристик имеет следующий вид
Рис.1.7.
Проведем моделирование временных динамических характеристик рассмотренных выше звеньев в MATHCAD 7.
Моделирование временных динамических характеристик безынерционного звена в MATHCAD 7 не представляет трудностей и интереса. Они совпадают с входным ступенчатым и импульсным воздействиями, умноженным на коэффициент передачи k.
Получим эти характеристики для апериодического звена. Для этого необходимо решить в MATHCAD 7 дифференциальное уравнение (1.2), используя функцию rkfixed(y,a,b,N,D). С помощью функции rkfixed решение уравнения ищется численно методом Рунге-Кутта четвертого порядка. Результатом является матрица, содержащая два столбца. В первом столбце расположены точки, в которых ищется решение дифференциального уравнения. Во втором столбце располагаются значения решения уравнения в этих точках.
Аргументами функции rkfixed(y,a,b,N,D) являются:
y - вектор начальных условий размерности n, где n - порядок дифференциального уравнения или число уравнений в системе, при решении системы дифференциальных уравнений n-го порядка;
a и b - граничные точки отрезка, на котором ищется решение, причем, вектор начальных условий y соответствует значению решения в точке a;
N - число точек не считая начальной, в которых ищется решение, при этом число строк в матрице решения равно N+1;
D(x,y) - вектор-функция размерности n, содержащая первые производные неизвестных функций.
Программа получения переходной характеристики апериодического звена имеет вид.
Сформируем единичное ступенчатое воздействие на отрезке времени от 0 до 1 сек. с шагом 0, 01 сек.
Зададим значения коэффициентов апериодического звена
Зададим начальное значение для y как нулевой элемент вектора размерности n=1.
Определим функцию D, задающую производную
Найдем матрицу решения
Построим график искомого решения в 101 точке
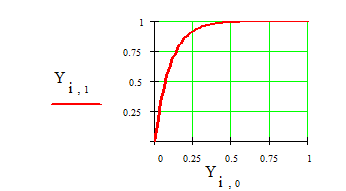
Рис.1.8.
Полученная переходная функция соответствует идеальной
. (1.9)
Заменив в рассмотренной программе блок формирования единичного ступенчатого воздействия на блок формирования импульсного воздействия нетрудно получить приближенную импульсную переходную характеристику апериодического звена.
Рис.1.9.
По характеру поведения она соответствует реальной
, (1.10)
отличие будет наблюдаться в точке
.
Заметим, что значение 
может быть при моделировании получено другим, если взять иную амплитуду входного импульсного воздействия и другое количество точек N в решении дифференциального уравнения.
Получим теперь переходную характеристику колебательного звена.
Сформируем единичное ступенчатое воздействие
Зададим значения коэффициентов колебательного звена
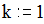
Зададим начальное значения для вектора y
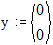
Определим функцию D, задающую производные приведя дифференциальное уравнение 2-го порядка к системе 2-х дифференциальных уравнений 1-го порядка
Найдем матрицу решения
Построим график искомого решения
Рис.1.10.
Заменив в программе блок формирования единичного ступенчатого воздействия на блок формирования импульсного воздействия получим приближенную импульсную переходную характеристику колебательного звена.
Рис.1.11.
Подобным образом могут быть получены переходная Рис.1.12 и приближенная импульсная переходная характеристики консервативного звена Рис.1.13, характер которых одинаков.
Рис.1.12.
Рис.1.13.
Переходная характеристика апериодического звена второго порядка при =2 имеет вид
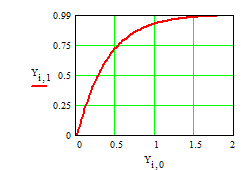
Рис.1.14.
И приближенная импульсная переходная характеристика
Рис.1.15.
Переходную характеристику интегрируюшего звена можно получить, проведя моделирование по следующей программе.
Сформируем единичное ступенчатое воздействие
Зададим значение коэффициента передачи интегрирующего звена
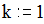
Зададим начальное значения для y
Определим функцию, задающую производную
Найдем матрицу решения
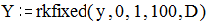
Построим график искомого решения
Рис.1.16.
Проближенная импульсная переходная характеристика интегрирующего звена в MATHCAD 7 имеет вид
Рис.1.17.
Для дифференцирующего звена
(1.11)
и
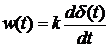. (1.12)
Для приближенного моделирования временных динамических характеристик дифференцирующего звена невозможно воспользоваться операторами дифференцирования, имеющимися в MATHCAD 7, так как дифференцируемая функция имеет разрыв при t=0. Однако заменив оператор дифференцирования разностной схемой
, (1.13)
можно осуществить моделирование временных динамических характеристик дифференцирующего звена.
Приведем программу получения переходной функции дифференцирующего звена.
Сформируем единичное ступенчатое воздействие
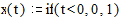
Запишем разностное уравнение, моделирующее работу звена, приняв
Получим переходную характеристику
Рис.1.18.
Моделирование импульсной переходной характеристики дифференцирующего звена дает следующий результат
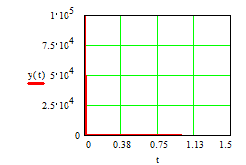
Рис.1.19.
При подаче на вход рассмотренных элементарных динамических звеньев ограниченного сигнала, сигнал на выходе таких звеньев будет также ограничен, за исключение интегрирующего звена. Существуют звенья у которых при подаче на вход ограниченного сигнала, сигнал на выходе неограниченно возрастает. Они относятся к неустойчивому типу звеньев, так как корни их характеристических уравнений лежат справа от мнимой оси и составляют группу так называемых неминимально-фазовых звеньев. Так для апериодического звена (1.2), неминимально-фазовое звено будет описываться следующим уравнением
, (1.13)
а для колебательного -
, (1.14)
или
. (1.15)
Например, полученная в MATHCAD 7 переходная характеристика звена (1.13) имеет тенденцию неограниченного роста
Рис.1.18.
Задание на лабораторную работу
а) Для апериодического звена получить временные динамические характеристики при следующих исходных данных
Таблица 1.1
| k | 0.5 | 1 | 2 |
| T | 0.1 | 0.2 | 0.3 |
Оценить влияние на эти характеристики параметров звена k и T.
б) Для колебательного, консервативного и апериодического звена 2-го порядка при исходных данных, приведенных в таблицах 1.2 и 1.3. получить временные динамические характеристики.
Таблица 1.2
x 
| 0.5 | 0.5 | 0.5 |
| k | 0.5 | 1 | 2 |
| T | 1 | 0.2 | 0.3 |
Таблица 1.3
| x | 0 | 0.1 | 0.5 | 0.8 | 1 | 2 |
| k | 1 | 1 | 1 | 1 | 1 | 1 |
| T | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
Оценить влияние на эти характеристики параметров звена k,T и x.
г) Для интегрирующего звена при k=1, 10 и 100 получить временные динамические характеристики. Оценить влияние на вид этих характеристик коэффициента передачи k.
д) Для неустойчивого колебательного звена при k=1, T=0.01 и x=0,1 получить переходную характеристику. Сравнить ее с аналогичной характеристикой устойчивого колебательного звена.
3. Отчет по лабораторной работе
Отчет должен содержать:
- cхему моделирования;
- уравнения звеньев;
- программы моделирования;
- полученные временные динамические характеристики;
- выводы. В выводах должна быть дана оценка влияния коэффициентов исследуемых звеньев на вид временных динамических характеристик.
Вопросы для самопроверки
1) Какое устройство называют элементарным динамическим звеном?
2) Какие Вы знаете звенья?
3) Напишите уравнения звеньев и какие параметры в них входят?
4) Какие входные воздействия подаются на вход звена для получения временных динамических характеристик и как эти воздействия могут быть получены в MATHCAD 7.
5) Какие существуют временные динамические характеристики?
6) Как в MATHCAD 7 моделируется работа апериодического звена?
7) Дайте определение переходной функции.
8) Дайте определение импульсной переходной характеристики.
9) Как в MATHCAD 7 моделируется работа колебательного звена?
10) Как влияет на временные характеристики величина постоянной времени, коэффициента передачи, коэффициента демпфирования звена?
