Мы строим 4 подграфика в одном окне, для этого используем функцию subplot, в которой задается разметка подграфиков и номер подграфика, к которому мы обращаемся. Сначала мы построим 4 графика, нанесенные линией, а после нанесем на них маркеры.
Итак, задаем количество точек на отрезке(который задан в пункте а), вектор точек Х и значения У в Х.(для графика и полинома)

После обращаемся к нужномуподграфику и строим его, выбирая цвет и правильно оформляя. Цвет и форма маркеров задаются в кавычках после координат в функции plot.
Аналогично для остальных 3х.

Теперь необходимо нанести маркеры, для этого выбираем количество точек в отрезке, равное 10, и делаем то же самое.

Главное не забыть указать форму маркера

Результат:

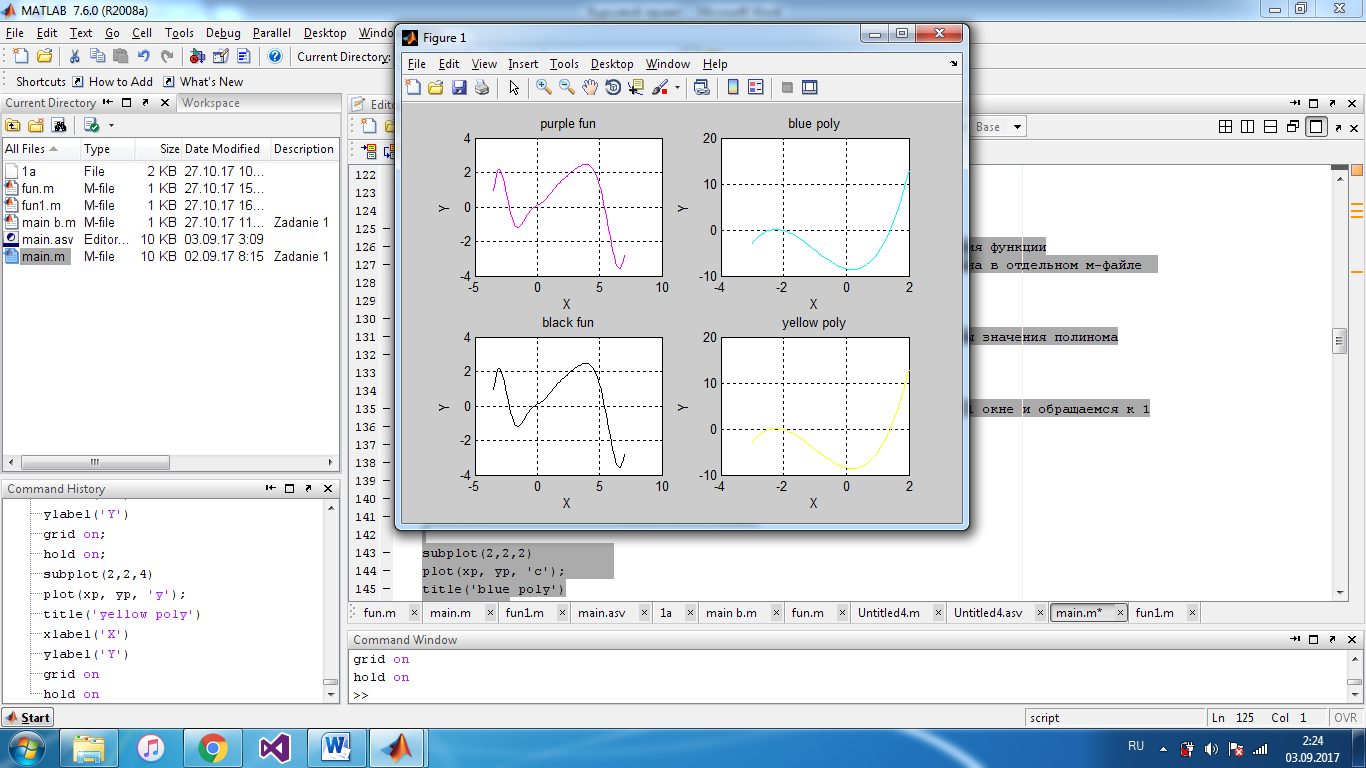
C) Построить графики всех функций в одних осях (4 подграфика) без характерных точек и с характерными точками без подписей.
Мы снова используем функцию subplotи делаем 4 подграфика. Сперва задаем количество точек и вектор Х, а также значения У для всех 4 подграфиков.Сперва мы будем строить пустые графики потом наносить маркеры на необходимые точки. Все действия делаются точно так же как и в прошлых пунктах.

1 подграфик строим с корнями
Сначала строим функцию и полином без характерных точек.

Находим и наносим маркеры на корни функции

Обозначаем корни полинома

Делаем легенды для того, чтобы понимать где какой график

Вот что получилось

Теперь сделаем графики с минимумами
Пустые графики

Минимумы функции

Минимумы полинома. Когда мы находим корни второй производной, мы ищем сразу максимумы и минимум без разбора, поэтому зная, что на данном промежутке экстремума всего 2, мы обращаемся к нему через индекс.

Не забываем про легенду

Результат:

Теперь нам нужно сделать подграфик с максимумами
Пустые графики с легендой

Максимумы функции через обратную функцию
Максимумы полинома. Снова обращаемся уже к 1-му элементу вектора корней.

Результат:

Теперь нам осталось построить только подграфик без характерных точек

Запустив все сразу у мы должны получить окно с 4-мя подграфиками одновременно:

Графики функции одной переменной с разрывом и кусочно-заданной функции
Теперь мы работаем со следующей функцией:

,где y(x) и  это функция и полином из первого задания
это функция и полином из первого задания
1.a)Построить график на интервале [x01, x02], содержащем корень полинома Рк(х) и нанести асимптоту в точке разрыва.






