a) Построить графики каждой функции в своих осях с нанесением характерных точек (корней, локальных экстремумов и точек перегиба (для полинома) – не более 3-х точек одного типа и не менее 2, если их несколько)
1.Функция
Сама функция:

Сначала зададим границы отрезка, на котором строится функция. А также зададим вектор х, количество элементов в котором равно количеству точек на заданном отрезке

После следует задать данную в задании функцию в отдельном м-файле.

Теперь мы можем задать зависимость у от х и построить график.

Не забываем правильно оформить наш график, используя названия, подписи осей, а также сетку. После нужно использовать функцию holdon для того, чтобы удержать график, и на него было можно наносить маркеры, текст и т п.

Вот, что у нас получилось. Теперь нам нужно найти и построить корни и точки экстремума этой функции.
Начнем с корней.
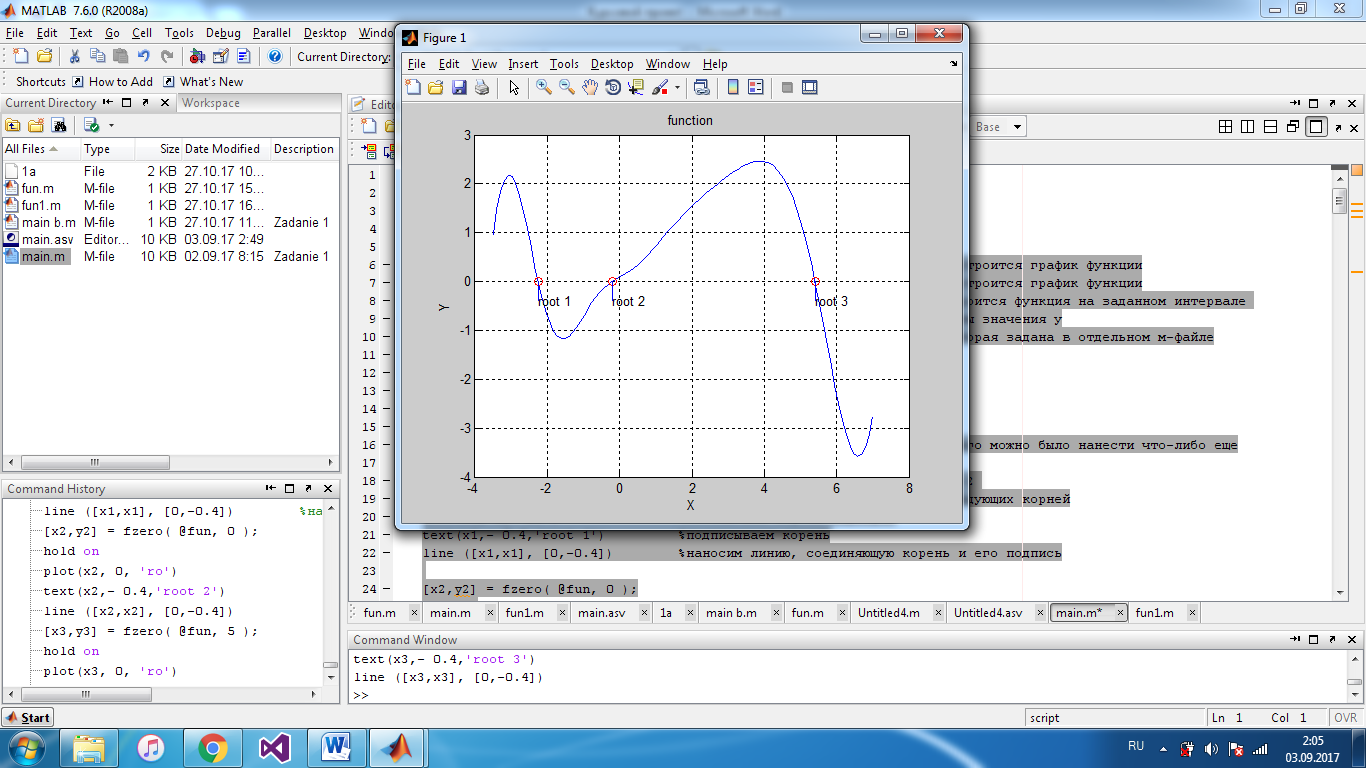
Для поиска пользуемся функцией fzero. Мы смотрим на график, приблизительно прикидываем, где может быть корень и запоминаем число рядом с корнем. Далее мы можем найти ближайший к этому числу корень.
После наносим маркер на корень, задав в кавычках форму и цвет маркера.

Не забываем добавить подпись и выносные линии к маркеру.

На нашем графике корня всего 3

Теперь найдем и построим экстремумы.
Начнем с минимумов. Алгоритм их поиска схож с алгоритмом поиска корней. Мы смотрим на график. Прикидываем на глаз минимальное значение и находим его, выбрав близкое к нему число через функцию fminsearch.

Не забываем про правильное оформление, сделав подписи и выносные линии.

На выбранном промежутке всего минимумов у функции 2

Теперь осталось найти максимумы
Для этого надо создать функциюfun1, равную –funв отдельном файле

Все остальное делаем аналогично минимуму
Только при нанесении маркеров и подписей используем отрицательное значение y, так как fun1 = -fun

Всего максимумов получилось 2

В итоге график со всеми характерными точками выглядит следующим образом:

Полином
Сначала задаем параметры полинома, границы отрезка, на котором строится график, а также количество точек на заданном отрезке.

После задаем вектор х, и берем от него значения ус помощью функции polyval

Строим график

Не забываем про правильное оформление

Вот как он выглядит

Теперь нам нужно найти корни полинома. Для их поиска используем функцию roots
Далее находим значения полинома в корнях для проверки

Остается только нанести маркеры на корни

Теперь подпишем наши корни и соединим подписи с маркерами

Теперь нам нужно найти минимумы и максимумы полинома – это корни второй производной.

Теперь берем значения полинома в найденных точках и наносим маркеры

Правильно оформляем

Найдем точки перегиба. Это корни второй производной. Поэтому повторяем те же действия, взяв производную от первой производной полинома.

Результат:





