Ранее мы рассмотрели цепь с последовательным соединением реактивных элементов L и С. Теперь рассмотрим цепи, где реактивные элементы соединены между собой параллельно.
Параллельное соединение двух реальных катушек
На рис. 66 показано параллельное соединение двух реальных катушек (двух цепочек RL). Для анализа работы схемы рассмотрим векторную диаграмму. В цепях с параллельным соединением элементов построение диаграммы всегда начинается с вектора напряжения Uоб, поскольку напряжение одинаково на всех параллельных участках. Затем строятся вектора токов в ветвях: I1 и I2. Как было рассмотрено ранее, токи I1 и I2 в цепочках RL отстают по фазе от напряжения U на углы φ1 и φ2.
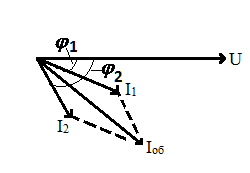
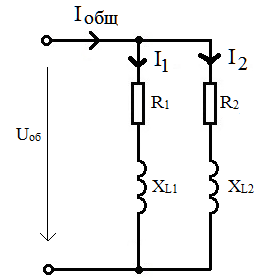
Рис. 66. Схема и векторная диаграмма для параллельного соединения двух катушек
Величину токов в ветвях можно найти по закону Ома:
; 
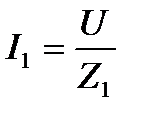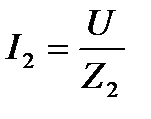, где Z – полное сопротивление соответствующей цепочки RL. Полное сопротивление цепочки RL находим по формуле: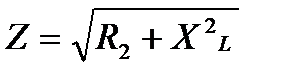 
Кроме величины тока в ветвях, для построения векторной диаграммы необходимо знать величины углов φ. Узнать величину угла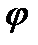 
можно, предварительно вычислив значение косинуса этого угла:
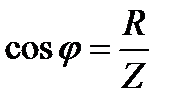
Зная величину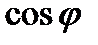 
, найдем величину угла φ, используя инженерный калькулятор или таблицы Брадиса.
Общий ток Iобщ, потребляемый схемой, найдем, суммируя вектора токов I1 и I2 по правилу параллелограмма. Арифметически суммировать токи в ветвях нельзя.
Параллельное соединение цепочек RL и RC
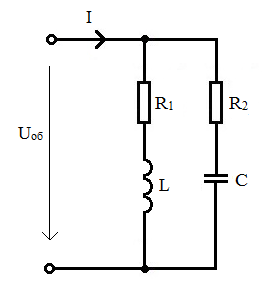Параллельное соединение цепочек RL и RC показано на рис. 67. Векторная диаграмма для этой схемы строится почти так же, как для предыдущей схемы. Разница лишь в том, что ток I2, в цепочке с ёмкостью, опережает приложенное напряжение по фазе.
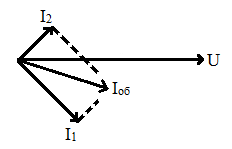
Рис. 67. Параллельное соединение цепочек RL и RC.
Векторная диаграмма для случая преобладания индуктивности
Расчетные формулы для вычисления токов в ветвях аналогичны предыдущей схеме:
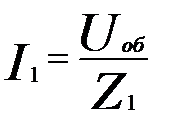
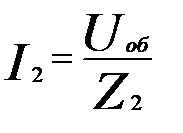
В данной цепи одновременно работают элементы L и С, обладающие, как известно, противоположными свойствами. Обычно один из этих элементов преобладает. На рассмотренной диаграмме преобладает индуктивность. Это видно из того, что общий ток отстает по фазе от напряжения, как это бывает в цепи с индуктивностью.
Резонанс токов
В цепи с параллельным соединение элементов L и С тоже может возникать резонанс. В этом случае он называется резонансом токов. Резонанс токов возникает в схеме, показанной на рис. 67, где цепочки RL и RC соединены параллельно.
Напомним, что резонансомназывает режим, когда цепь содержит реактивные элементы, но ведет себя, как активное сопротивление. Это объясняется тем, что L и С, обладая противоположными свойствами, взаимно компенсируют друг друга. При этом вся цепь приобретает свойства активного сопротивления.
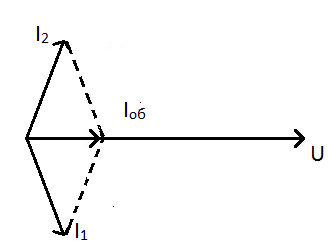
Рис. 68. Векторная диаграмма цепи в режиме резонанса токов
Векторная диаграмма для цепи в режиме резонанса токов показана на рис. 68. Диаграмма строится в соответствии с принципами, рассмотренными в разделе "Параллельное соединение двух реальных катушек". Видно, что общий ток Iоб, потребляемый цепью, равен векторной сумме токов в ветвях и совпадает по фазе с приложенным напряжением.
Свойства цепи при резонансе токов в многом схожи со свойствами цепи при резонансе напряжений:
1) условие возникновения резонанса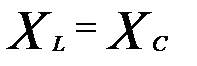 
остаётся тем же (при условии равенства активных сопротивлений в ветвях схемы);
2) добиться резонанса можно меняя индуктивность L, или меняя ёмскость конденсатора С, или меняя частоту приложенного напряжения U;
3) резонанс наступает на частоте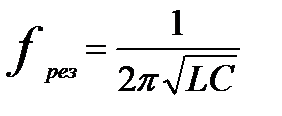 
;
4) угол φ сдвига по фазе между приложенным к схеме напряжением и током, потребляемым схемой, равен нулю, т.е. ток совпадает по фазе с приложенным напряжением. Это показано на рис. 68.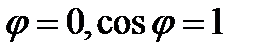 
, где φ – угол между током и общим напряжением.
В то же время по ряду свойств резонанс токов отличается от резонанса напряжений:
1) общий ток Iоб, в режиме резонанса, принимает минимальное значение; их диаграммы видно, что общий ток меньше любого из токов в ветвях;
2) поскольку ток минимальный, общее сопротивление схемы становится максимальным.
