Цель работы.
Цель работы заключается в ознакомлении с моделью обслуживания летательного аппарата и характеристиками системы контроля в системе массового обслуживания, в построении модели массового обслуживания в виде графа состояний, составлении и решении дифференциальных уравнений графа, получении и анализе основных характеристик системы контроля.
Задание.
По заданному графу составить систему дифференциальных уравнений и решить её для установившегося и переходного режимов. Получить основные характеристики системы контроля (СК) и провести анализ характеристик. Оценить целесообразность использования полученного графа модели массового обслуживания.
Исходные данные.
Задан граф системы массового обслуживания, состоящий из семи состояний. Рассматривается режим предстартовой подготовки на земле перед полётом.
Граф представлен на рис. 1.
| H2 |
| H1 |
| H7 |
| H5 |
| H3 |
| H4 |
| H6 |
| η 1 |
| λ хр |
| α |
| D1 |
| D0 |
| β |
| η |
| γ α |
| η 2 |
| γ0 |
| Ремонт |
| γ11 |
| γ1 |
| γ β |
| γ ββ |
Рис. 1. Граф состояний системы обслуживания
H1 – вероятность того, что объект контроля (ОК) полностью работоспособен, но ждёт контроля, в режиме ожидания;
H2 –появление ложных отказов;
H3 –режим ожидания полёта, произошёл отказ;
H4 –характеристика вероятности появления риска заказчика;
H5 –восстановление, ремонт;
H6 –правильное обнаружение отказов в объекте контрольной аппаратурой;
H7 –вероятность принятия решения, что объект исправен.
Заданы следующие интенсивности перехода из одного состояния в другое:
1) λ хр= 10^-4 – интенсивность отказов ОК в режиме простоя;
2) γα = 10^-6 – интенсивность перевода исправных ОК-СК в режим восстановления;
3) γ β = 10^-8 – интенсивность перевода неисправных ОК-СК в режим восстановления;
4) γ ββ = 0,033 – интенсивность перевода неисправных ОК-СК в режим восстановления;
5) γ0 = 0,1 – интенсивность перевода неисправных ОК-СК в режим восстановления;
6) γ1 = 0,1 – интенсивность перевода неисправных ОК-СК в режим восстановления;
7) γ11 = 1 – интенсивность перевода неисправных ОК-СК в режим восстановления;
8) η = 0,5 – интенсивность восстановления неисправных ОК и СК;
9) η1 = 10 – интенсивность восстановления неисправных ОК и СК;
10) η2 = 1 – интенсивность восстановления неисправных ОК и СК.
Время ожидания: Тожид = 2000м.
Время контроля: Тконтр = 1 ч.
Система дифференциальных уравнений графа для нестационарного режима.
Дифференциальные уравнения для вероятностей перехода в каждое состояние для системы:
= - (λ хр + γ0 + γα) P1(t) + η1 P2(t) + η P5(t) + η2 P7(t),
= γα P1(t) - η 1 P2(t);
= λ хрP1(t) - (γ 1 + γ β) P3(t);
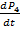= γ β P3(t) - γ ββ P4(t);
= γ ββ P4(t) - η P5(t) + γ 11 P6(t);
= γ 1 P3(t) - γ 11 P6(t);
= γ 0 P1(t) - η 2 P7(t).
P1(0) = 1; P2(0) = 0; P3(0) = 0; P4(0) = 0; P5(0) = 0; P6(0) = 0; P7(0) = 0.
Формулы для вычисления риска изготовителя α, заказчика β и достоверностей канала «годен» D 0 и «негоден» D 1:
D 0 = 
D 1 = 
,
α = 
,
β = 
;
K г= 
.
K г - коэффициент готовности(вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается)
