Х'Арİискаιа Арифметика 1 курсъ. 1 урокъ
Тема: Знаки и Системы
Предмет на котором вы научитесь считать образами. Кстати, заметьте, наши Прѣдки не использовали как сейчас компьютеров, калькуляторов, и прочих, будем говорить счетно-вычислительных безобразий. Они пользовались одним единственным компьютером, который у них был – это голова. Поэтому все вычисления проводились в уме. Использовались совершенно разные системы.
Поэтому, я напомню вам первый класс школы, когда вы учили таблицу умножения. Два умножить на два – четыре, два умножить на три – шесть, да? Но, когда говорили про три, у вас было трижды три, трижды четыре, да? Когда дошли до цифры пять, у вас умножение почему-то стало пятью: пятью два, пятью семь, пятью девять. Т.е. и никто из учителей не объяснил почему при умножении используются совершенно разные названия. А в обиходе слышали: три по пять. Т.е. заметьте, я сейчас привел четыре вида умножения:
· умножение на;
· умножение жды;
· умножение ю;
· умножение о.
Но это как бы структурные, но еще было множество других умножений. Допустим, ровное умножение, когда считались какие-то ровные числа., ровные объёмы. Т.е., что для этого необходимо было?- как, что, для чего считать. И заметьте, в школе написали три в кубе, три в третьей степени.
33
Три чего, какой степени, чего это, точек, дров, угля, молока, нефти, газа, чего? Т.е. абстрактные цифры, которые не несут в себе никакого образа. Но, наши ж Прѣдки знали, как это всё просчитать. Как, для чего чтобы совместить образ, чтобы было понятно – и считать легче. То ли вы какие-то аморфные цифры считаете, да?– и путаетесь. Но когда вы считаете, допустим, вещи, у вас уже не будет путаницы. Допустим, пересчитали у ребенка, 10 беленьких рубашек, да, 5 цветных, 4 черных, т.е. вы знаете, у ребенка 19 рубах. Но этих для школы ему – десяток, цветных – по улице гонять, и черные на всяких пожарный, траурный случай, ну или может ребенок по жизни чернорубашечник J. Но, здесь-то вам проще разобраться, чем 10+5+4. чего 10, чего 5, а чего 4. Поэтому дети очень трудно воспринимают, что сейчас им преподается с первого класса, математику. Я по себе знаю, когда мы учились, первые три класса у нас была вообще-то арифметика. Арифметика, которую потом при Брежневе обменили,- это числинница. Но, числинница образов. А здесь мы будем изучать хАрiискую арифметику. Т.е. счисляемые образы, которые хАрiицы использовали. И заметьте, для чего, почему именно хАрiискую? Не дарийскую арифметику, не рассенскую, не святорусскую, а именно хАрiискую? Потому что, хАрiискаιа, она охватывает и те все три в себя, и плюс, она охватывает, если те, будем говорить для определенного мира считали, то хАрiискаιа она охватывает и другие пространственные измерения. Понятно, да? И при помощи её можно просчитывать и другие временные структуры, и объёмные, и пространственные, различные.
Но для того, чтобы разобраться, какой знак определяет, видели я написал "33". Что это конкретно? После него всегда ставился знак опреления. Мы должны же определиться. Не как современные математики. Которые не знают, что такое точка, что такое линия, что такое круг, что такое окружность. Они могут это как-то описать, но что конкретно означает, определить данную структуру они не могут. К какой системе она относится? Поэтому, мы и записываем как подтему, азы, чтобы понять:
Знаки хАрiискаго определения.
Т.е. вы можете сразу заметить – две и. Но, одна имеет вселенское значение (прим. "i"), охватывает всю Вселенную. А значит что, раз всю Вселенную, значит все её времена, пространства, измерения, все структуры. И плюс, что стоит – "и" – состояние равновесия, или как многие сравнивают – состояние без войны. Но без войны, т.е. без конфликтов, без противодействия. И окончание в русских и славянских языках, наречиях было на "аго". Это в советское время сделали на "ого". Уяснили?
Т.е. какие же знаки хАрiискаго определения Ван необходимо знать?
В первую очередь,
| + | сложение, соединение |
| − | вычитание, изъятие |
| ÷ | раздъление |
Та же черта, заметьте, вычитать что-то, значит убрать. Мы опять ставим знак вычитания (прим, "-"), или как мы иногда говорим "вычисления", т.е. вычислить что убрать. И ставим две точки. Это у нас разделение. Т.е. посмотрите на само начертание. Черта как бы точки между собой разделила. Т.е. мы как бы вычли: одно сюда, одно сюда. Т.е. мы их разделили как бы на соответствующий порядок.
Но опять – что же такое точка? Точка – это какая-то определенная структура. Поэтому, когда мы структурированное вычисление делаем, мы ставим именно точку, и пишем умножение, и большими буквами НА, буквицу Наш и буквицу Азъ.
| • | умножение НА (двухмерное) |
Вы имеете что?- две славянские буквицы:
· Азъ – это Богъ живущий на Земле.
· А здесь стоит Наш
Т.е. умножение наших Боговъ которые жили на Земле. А раз они жили на Земле, т.е. на какой-то плоскостной форме они проводили свои вычисления. Правильно? Т.е. простые вычисления. Поэтому умножение НА – двухмерное.
Но, заметьте, я поставлю одну точку, и через неё проведу четыре линии, четыре пространственные координаты.
Î
У меня получился крестик. Т.е. заметьте, я уже рассказывал, что у нас мир, помните, в юджизме?- как бы трёхструктурированный. Но вот эта троичная структура, она как бы покоится на четвертой – три слон на черепахе. Здесь то же самое, как бы мы сказали: глубина, длина, а длина это куда наш взор на всю длину повернулись, высота и одновременно во времени. Т.е. оно же всё происходит, течет. Поэтому мир наш называют четырехмерным. Не трёхмерным, как правило, а трёхмерным в четыре … Поэтому, как для обихода, это у нас умножение ЖДЫ
| Î | умножение ЖДЫ (трёхмерное) |
Буквица Живете, Жизнь, дальше стоит Добро, т.е. в совокупности и стоит Еры – подчиненный определенным законам. Т.е., что-то доброе созданное в жизни и подчиненное определенным законам.
Т.е. это у нас всё определенное законами Яви. Поэтому это у нас всё трёхмерное, ну во времени. Потому, что любое действие, которое мы будем производить, оно то же будет последовательно идти во времени. Но мы как бы считаем определенные пространственные характеристики. Ибо, знаете, как говорят. Чтобы человека не путать со временем, детям объясняют просто: вот эти четыре луча, это глубина, длина, ширина и высота. Но понятие ширина и длина у славян взаимосвязано. Я смотрю в эту сторону (прим, прямо), вот для меня длина (Отче указал рукой прямо), вот ширина (указал рукой направо). Я повернулся сюда (прим, направо) – они поменялись местами. Т.е. это что?- плавно перетекающие структурные характеристики.
Дальше. Я оставляю эти же характеристики и разделяю их самих к себе.
| * | умножение Ю (объёмновременное) |
Т.е., если здесь (прим, ÷) я разделял порядки разных структур, то здесь я явные порядки разделяю. А значит, если я делю на равные структуры. Значит они мне дают что?- трёхмерное это объём, а здесь объём разделен во времени. И вот это у нас будет умножение Ю, объёмновременное, т.е. пространственное. Т.е. посмотрите внимательно (прим, на букву Ю), у нас есть круг, сфера, объём, есть то, что находится вне его, поэтому я говорю: объёмновременное, оно же пространственное. Т.е., мы как бы находясь на сфере воспринимает плоскость, а находясь на плоскости воспринимаем сферу. Простой пример, наш земной шар круглый, но его поверхность мы воспринимаем как плоскость. Ясно, да? Или, например, луна в небе, она же объёмная, но мы её воспринимаем плоской.
Т.е. остальные знаки определения умножения мы не будем пока ставить, мы их будем разбирать гораздо позже. Вам головной боли и проблем хватит с этими трёмя видами умножения.
Следующий знак,
| = | равенство |
Две тождественные черты, которые означают равенство. Вот заметьте, если здесь у нас вычитание (прим, "-"), то здесь (прим, "=") у нас уже вычли и высчитали, т.е. то что у нас получилось обоюдно по этому и по этому. Поэтому знак называется "равенство". Я вам сразу же объясняю как воспринимать данный знак. Не потому что равенство пишется "=" – две черточки. А почему? Заметьте, вот мы структурно нарисовали знак равенства. Но заметьте, может быть равно два каких-то объёма, а могут быть они не равны. Объясняю. В одной бутылке литровой налит вишневый сок, а в другой литровой бутылке налито молоко. Они равны между собой по объёму, но не равны по значению. Т.е. значит что?- у них вводится еще одна вычислительная характеристика. Поэтому раз они не равны, а тождественны, значит они что?- определенной структуре соответствуют.
Поэтому я к равно ставлю третью черту – это еще один знак. И вот этот знак соответствия.
| ≡ | соответствие |
Ну, допустим, +5 он не равен -5, но он ему соответствует. Почему? Потому что на пространственной оси координат +5 и -5 они соответствуют равноудаленности от какой-то определенной точки, т.е. они соответствуют по определенным положениям, законам и структурам. Понятно, да?
Следующий знак. Структурно, допустим, они не похожи. Т.е. с виду они, налит томатный сок в бутылке и морковный сок. По виду они из далека похожи, бутылки – непонятно, то ли 0,5 то ли 0,6. Поэтому их соответствие, т.е. равенство только визуально, но на самом деле оно искажено, поэтому и линии вроде бы схожи, но искажены. Поэтому, ставим знак "примерность".
| ≈ | примерность, приближенность |
Знак примерности или приближенности. Они как бы приближены, но таковыми не являются. Допустим Денисов – приближенный главы государства. Но он же не является главой государства. И заметьте, ну допустим, две бутылки литровых молока. Если мы поставим их на чашу весов, они и весить будут и по объёму одинаково. Т.е. там мы можем сказать, что они равны. Но как равенство?- молекулярный состав у них может быть разный. Так? А одна бутылка может быть с утренней дойки, другая – с вечерней. Поэтому разлиты они будут с разных фляг. Значит они уже как бы не равны по внутреннему составу. Но, дала их одна и та же корова, одна и та же посуда, один и тот же объём. И что мы говорим?- они между собой "гармонизированы".
| 1 | гармонизировано |
Так же как +5 и -5 гармонизированы относительно центра, т.е. относительно какой-то структуры они между собой гармонизированы.
Следующий знак. Заметьте, я ставлю знак разделения, который соприкасается со знаком соответствия.
| ÷/ ≡ | взаимодействие соответствий |
Т.е. они не просто соприкоснулись. Этот знак означает взаимодействие соответствий. Т.е. то, что соответствует друг другу между собой может и взаимодействовать.
Дальше. Знак, который вы все знаете. У нас он называется проекция.

| проекция, отображение |
Следующий знак, который тоже использовали в арифметике, в математике – две широко расставленные черты, между которыми что-то вписывали. Но, в современной математике это называется модуль. А у нас это не модуль. Это называется ограниченное пространство, грани.
| ││ | ограниченное пространство, грани |
И еще система, с которой вам придется – мерное титло. Есть числовое титло - используется для записи буквицы в числовом режиме. Мерное титло – это определенные меры пядевой системы.
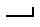
| мерное титло |
А вот это числовое титло

| числовое титло |
У славян буквицы несли числовое значение. Не цифровое, числовое. У нас были числа, а цифири были у библейского народа. Поэтому у нас числами управляет Числобог, а у них – Циферблат. У них дерево цифер называется дерево цифирот или сиферот, как многие неправильно. Цифирьециро – одна из книг каббалы. Т.е. видите. Они свое пытаются, или будем говорить принесли в наш язык. У нас есть сове – число. Цифры ввел Петр I.
И вот заметьте, титлованный азъ. В просторечии он читался как "ать": ать, два! Маршировать. Азъ – это Богъ живущий. И каждый говорил: "Азъ есьм", т.е. я как потомок Боговъ есть живу, существую. А выразить себя в числовой форме – числовое титло.
Пишем, как бы еще тему.
Системы умножения и их структурные проекции
Как и я сказал, мы будем охватывать всё. Поэтому раз структурные проекции – мы будем разбирать относительно каждой пространственной структуры, как она проецируется куда-то.
Ну давайте её отложим. Азъ и поставим.
│а│
Т.е. она у нас будет обозначать любую структуру и отображать любую проекцию. А теперь представьте: есть миры и пространства, есть миры с дробными пространствами, есть внепространственное что-то. И вот представьте, и это что-то внепространственное, оно же все равно имеет какую-то характеристику. Правильно? А как мы единое передадим вне всякого пространства? А это и будет та самая изначальная точка. Понятно, да? Хорошо, чтобы было понятней, я вам процитирую Книгу Света, харатья 1: "Некогда, вернее тогда, кода не было пространства и времен нами людьми воспринимаемых, был не воплощаясь Един Великий Рамха. Он проявился в новую действительность и от восприятия новой бескрайней бесконечности озарился великим светом радости". Т.е. видите, Веды говорят что было такое состояние, когда не было времен и пространства. Значит что-то было безвременное и безпространственное. Но заметьте, он проявился в новую действительность. А это о чем говорит? Что где-то была старая действительность, где он, возможно, был не один. Ну, наткнулся он на новую действительность и от него пошел Свет, и появились новые Вселенные. Т.е. это та самая точка. Которую ученные называют точкой сингулярности,т.е. когда, вся вселенная или что бы то ни было, была когда-то в единой, непространственной структуре. Только они до сих пор и не знают, кто поднес спичку, у них же до сих пор идея вселенского взрыва. А это просто не воплощаясь Рамха проявился и вот свет радости, поток Инглии, он наполнил жизнью и жизнь появилась. Вот она единая точка. Т.е. как бы в нулевом, безпространственном, я его поставил как бы сферическое проявление. Азъ, он был един не воплощаясь.
│а│º = 1
Т.е. как бы Азъ в нулевом это есть единый, изначальный.
Ну потом, свет пошел, начал соединять. Азъ появилась первая пространственная характеристика, которую начал наполнять свет.
│а│1
И заметьте, и как только свет, Инглия, истек, он начал наполнять, и в этот момент, как говорят Веды, в новой действительности появилось Великое Сверхгигантское Нечто. А так как оно не было тем, чем являлся Великий Рамха, значит она стала точкой противоположности. А если есть что-то одно и ему противоположное, это чему равно? Двум. Как бы светлое и темное.
│а│1 = 2
А теперь, мы запишем подправило: "Любая фигура, объект или структура одномерного пространства будет иметь две опорные точки".
И когда вы в школе изображали оси координат, вы что рисовали?- где-то минус бесконечность, где-то плюс бесконечность. И вот это плюс бесконечность – это положительное светлое, а минус как бы мрачное, уходящее во мрак. Все текло от плюса к минусу. И так же и в этой (прим. вертикальной) пространственной оси.
Далее. Вот мы перешли к двухмерному пространству. Вот сейчас мы перейдем к проекции. Т.е. мы имеем, что на сей момент – какой-то отрезок одномерного пространства. Чтобы получить его структурную характеристику в двухмерном пространстве, мы должны провести проекцию к длине отрезка и на длину данного отрезка.
И это я запишу следующим образом: "а" первого пространства, первой мерности спроецирован на "а" первой мерности. Сколько здесь у меня?- две мерности. И что у меня получилось?- четыре (рис.1)
 |
(рис.1) │а│2 = │а│1 ┴ │а│1 = 4
Т.е. мы получили проекцию квадрата, у которого 4 опорные точки.
Чтобы получить фигуру трёхмерного пространства мы должны "а" второе спроецировать на "а" второе. Объясняю, что мы делаем. Мы должны провести проекцию уже не к линии, к отрезку, мы должны провести проекцию квадрата на длину квадрата. И мы получили уже куб. и сколько опорных точек?- 8
│а│3 = │а│2 ┴ │а│2 = 8
А теперь посмотрите на свои формулы – определенная прогрессия. Т.е. чтобы получить четырехмерную фигуру мы должны что сделать?- мы должны провести проекцию третьей на длину третьей. Т.е. мы должны что?- спроецировать куб на длину куба (рис. 2)
 |
(рис. 2)
Таким образом, мы его проецируем разворачивая. И получилось 16 опорных точек.
│а│4 = │а│3 ┴ │а│3 = 16
Дальше идет принцип, который никто не отвергал. Многие говорят: "А чем вы докажете". - С компьютерами дело все имеют? Память. Сначала 4 Мб, потом появилось 8, потом 16. значит в пятимерном пространстве эта фигура будет иметь 32 опорные точки. В шестимерном пространстве – 64, в семимерном - 128, в восьмимерном – 256. (рис. 3)
 | a | 5 ≡ | a | 4 | a | 4 ≡ 32
| a | 5 ≡ | a | 4 | a | 4 ≡ 32
 | |||
 | |||
 | a | 6 ≡ | a | 5 | a | 5 ≡ 64
| a | 6 ≡ | a | 5 | a | 5 ≡ 64

(рис. 3)
Шестнадцатимерное пространство, оно есть следующее гармоничное пространство за нашим. Если у нас здесь открыты 16 каналов для того чтобы мы познали 16-мерное пространство, там-то у нас будет раскрыто 256. Это мы познаем. А структурная разверстка идет с увеличением, значит что?- 65 536 опорных точек. Всего!
И заметьте, куб сколько имеет?- 8 опорных точек. Когда говорим ЖДЫ, умножение, мы говорим о трёхмерности – дважды. А когда я говорю "два", значит два куба в пространстве.
Дважды два – шестнадцать. Дошло?
Потому что когда в школе вам сказали: два плюс два – четыре, дважды два – четыре, два во второй степени – четыре, вас два раза из трёх обманули. Два плюс два – четыре, дважды два – 16, а два во второй степени будет 3,99999999… - оно никогда не будет равно 4, потому что мерность нашего пространства не равно трём.
Пишем дальше тему.
Определение мерности при использовании четко структурных изображений
│а│2 = 3
(а = 3)
Раз оно трёхмерное, то я и изображаю вам данную четкую структуру. (рис. 4)
 |
(рис. 4)
 |
Т.е. здесь мы также занимаемся проекцией, только не в гармоничной форме, а в отображении к четкой структуре. Поэтому (рис. 5)
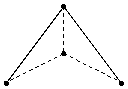
 (рис. 5) | а | 3 = 4
(рис. 5) | а | 3 = 4
Чтобы получить 4-мерную фигуру я должен что сделать?- спроецировать структурно данную фигуру. (рис. 6)
 |
(рис. 6) | а | 4 = 5
И у меня получилось что?- два тетропака соединены между собой.
А теперь | а | 5: (рис. 7)
 |
|
|
|






 | а | 5 = 9 (точка №1 является общей для обоих проекций)
| а | 5 = 9 (точка №1 является общей для обоих проекций)
 | |||
| |||
(рис. 7)
Дальше, 6-тимерная: (рис. 8)
 |







 | а | 6 ≡ | а | 5 | а | 5 - 2 (общие точки) ≡ 16
| а | 6 ≡ | а | 5 | а | 5 - 2 (общие точки) ≡ 16
 |
(рис. 8)
А теперь представьте семимерная: (рис. 9)
 | |||
 | |||



 | а | 7 ≡ | а | 6 | а | 6 ≡ 16 + 16 – 4 (общ.точки) ≡ 28
| а | 7 ≡ | а | 6 | а | 6 ≡ 16 + 16 – 4 (общ.точки) ≡ 28
 |
(рис. 9)
И вот на этой системе и построено умножение.






