Перевод десятичных чисел в двоичные

ИЗМЕРЕНИЕ И КОДИРОВАНИЕ ИНФОРМАЦИИ

Информация относится к фундаментальным, неопределяемым понятиям науки информатика. Тем не менее:

ü в быту информацией называют любые данные, сведения, знания, которые кого-либо интересуют. Например, сообщение о каких-либо событиях, о чьей-либо деятельности и т.п.;

ü в технике под информацией понимают сообщения, передаваемые в форме знаков или сигналов (в этом случае есть источник сообщений, получатель (приемник) сообщений, канал связи);

ü в теории информации под информацией понимают сведения об объектах и явлениях окружающей среды, их параметрах, свойствах и состоянии, которые уменьшают степень неопределенности, неполноты имеющихся о них знаний.

Применительно к компьютерной обработке данных под информацией понимают некоторую последовательность символических обозначений (букв, цифр, закодированных графических образов и звуков и т.п.), несущую смысловую нагрузку и представленную в понятном компьютеру виде. Каждый новый символ в такой последовательности символов увеличивает информационный объем сообщения.

1 бит — минимальная единица измерения информации. При вероятностном подходе к измерению информации это количество информации, уменьшающее неопределенность знаний в 2 раза.

Связь между единицами измерения информации:
• 1 байт = 8 бит;
• 1 Кб (килобайт) = 2¹⁰ (1024) байт = 2¹³ бит;
• 1 Мб (мегабайт) = 2¹⁰ (1024) Кб = 2²⁰ (1 048 576) байт = 2²³ бит;
• 1 Гб (гигабайт) = 2¹⁰Мб = 2²⁰ Кб = 2³⁰ байт = = 2³³ бит;
• 1 Тб (терабайт) = 2¹⁰ Гб = 2²⁰ Мб = 2³⁰ Кб = 2⁴⁰ байт = 2⁴³ бит.

Кодирование информации - это представление сообщений в конкретном виде при помощи некоторой последовательности знаков. Правило отображения одного набора знаков в другой называется кодом. Обычно кодированием называют перевод информации с «человеческого» языка на формальный, например, в двоичный код, а декодированием – обратный переход.

При кодировании информации для представления ее в памяти ЭВМ используется двоичный способ, т.е. любая информация — будь то числа, текст, графическое изображение, звук или видео — представляется универсальным двоичным кодом. Алфавит этого кода составляют символы 0 и 1. Этот способ кодирования был выбран потому, что технически реализовать два существенно различных состояния, представляющих, соответственно, 0 или 1, значительно проще, чем, например, три или десять. Действительно, отсутствие напряжения может обозначать 0, наличие — 1; отсутствие намагниченности участка носителя информации — 0, присутствие намагниченности — 1 и т.д. Каждая цифра машинного кода несет 1 бит информации.

Для кодирования одного символа используют 8 бит - один байт.

Байт - это наименьшая единица обработки информации. С помощью одного байта можно закодировать 2⁸=256 символов.

Существует таблица кодов символов. Первые коды с 0 по 127 являются стандартными и обязательными для всех стран и всех компьютеров.

Коды с 0 по 32  соответствуют операциям (перевод строки, ввод пробела и т.д.)

Коды с 33 по 127 являются  интернациональными и соответствуют символам латинского алфавита, цифрам, знакам арифметических операций и знакам препинания.

Коды с 128 по 225 являются национальными (в каждой стране разные), т.е. в национальных кодировках одному и тому же коду соответствуют различные символы.

Первую половину называют таблицей ASCII (Американский стандартный код для обмена информацией).

Для русских букв существует пять однобайтовых таблиц:

Windows, MS-DOS, КОИ -8, Mac, ISO.

Также разработан международный стандарт Unicode, в котором каждый символ кодируется двумя байтами.

ЗАДАНИЯ НА КОДИРОВАНИЕ ТЕКСТОВОЙ ИНФОРМАЦИИ

Задание 1

Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 16-битном коде Unicode, в 8-битную кодировку КОИ-8. При этом информационное сообщение уменьшилось на 720 бит. Какова длина сообщения в символах?

1) 90

2) 45

3) 180

4) 720

Решение:

Пусть в первоначальном сообщении х символов. Тогда его объем равен:

16 бит* х = 16х бит

В перекодированном сообщении количество символов не изменилось, т.е. оно также равно х, а вот его объем стал равен:   8 бит* х = 8х бит.

И этот объем меньше первоначального на 720 бит. Составим уравнение и решим его:

16х — 8х =720

8х = 720

х = 90

Ответ: 1

 Задание 2

В кодировке Unicode на каждый символ отводится два байта. Определите информационный объем слова из двадцати четырех символов в этой кодировке.

1) 384 бита;

2) 192 бита;

3) 256 бит;

4) 48 бит.

Решение:

24 * 2байта=48 байтов=384 бита

Ответ: 1

Задание 3

Текстовый документ, состоящий из 5120 символов, хранился в 8-битной кодировке КОИ-8. Этот документ был преобразован в 16-битную кодировку Unicode. Укажите, какое дополнительное количество Кбайт потребуется для хранения документа. В ответе запишите только число.

Решение. После перехода от 8-битной кодировки из 16-битного на каждый символ стало тратиться на 8 бит = 1 байт больше. На 5120 символов будет нужно больше на 5120*8 бит =5120*1 байт = 5120 байт = 5*1024 байт = 5 Кбайт.

Ответ: 5

Задание 4

Считая, что каждый символ кодируется 16 битами, оцените информационный объем следующей Пушкинской фразы в кодировке Unicode:

Привычка свыше нам дана: Замена счастию она.

1) 44 бита;

2) 704 бита;

3) 44 байта;

4) 704 байта.

Решение

Данное предложение содержит 44 символа (включая точку и двоеточие), то есть в кодировке Unicode оно содержит 88 байт или 704 бита.

Ответ: 2      

 

КОДИРОВКА ИЗОБРАЖЕНИЙ

 

Изображения на экране компьютера разбиваются на маленькие квадратики – пиксели. Чем больше пикселей, тем качественнее изображение. На мониторах обычно бывает 1024*768, 1280*1024 пикселей и выше.

Глубина цвета - это количество бит, которое используют для кодирования цвета одного пиксела. Для кодирования двухцветного (черно-белого) изображения достаточно выделить  один бит на представление цвета каждого пиксела. Для кодирования изображения с оттенками серого цвета (4 цвета) необходимо 2 бита (2² =4). Выделение одного байта позволяет закодировать 256 (2⁸ =256) различных цветовых оттенков. Два байта (16 битов) позволяют определить 65536 (2¹⁶ =65536) различных цветов. Этот режим называется High Color. Если для кодирования цвета используются три байта (24 бита), возможно одновременное отображение 16,7 млн цветов. Этот режим называется True Color. От глубины цвета зависит размер файла, в котором сохранено изображение.

Существует много различных типов цветовых моделей. Наиболее частодля графических изображений используется модель RGB.

 Каждый пиксель имеет свой цвет, который складывается путем смешивания трех основных цветов:

Красный      R ed      R

Зеленый      G reen      G       Палитра RGB

Синий          B lue        B

 

Различаются 256 оттенков каждого цвета: по номерам от 0 до 255. Значит, всего из 256 оттенков трех основных цветов можно образовать

2⁸ * 2⁸ * 2⁸ = 256 *256 *256 ≈16,7 млн. цветов.

Каждый оттенок основного цвета хранится в одном байте. Число 255 в двоичном виде представляется восемью единицами. Значит, цвет пикселя хранится в трех байтах. В графическом редакторе Paint цвет пиксела обычно задается тройкой чисел:

(0,0,0) - черный, в двоичном виде: 00000000, 00000000, 00000000

(255,255,255) - белый, в двоичном виде: 11111111, 11111111, 11111111

(255,0,0) - красный, в двоичном виде: 11111111, 00000000, 00000000

(0,255,0) – зеленый, в двоичном виде: 00000000, 11111111, 00000000

(0,0,255) – синий, в двоичном виде: 00000000, 00000000, 11111111

(0,128,128) - бирюзовый, в двоичном виде: 00000000, 10000000, 10000000

КОДИРОВКА ЧИСЕЛ

                                                        

Кодировка числовой информации в компьютере производится на основе представления привычных нам десятичных чисел в двоичной системе счисления. В компьютерах также используют шестнадцатеричную систему счисления (с/с).

Системой счисления называется способ записи чисел с помощью некоторого набора цифр.

Примеры:

1. Десятичная с/с                            основание= 10

                               

Набор цифр: 0,1,2, …, 9            Числа:          2, 301, …

 

2. Двоичная с/с                                основание= 2

                           

Набор цифр: 0,1                         Числа: 0, 1, 10, 101, …

 

3. Шестнадцатеричная с/с             основание= 16

 

           Набор цифр: 0,1,2, …, 9, A, B,C, D, E, F           Числа: 37, A5, F0

 

Все рассмотренные системы счисления являются позиционными, то есть значение каждой цифры зависит от ее позиции в записи числа.

Число в позиционной системе счисления можно представить в виде суммы произведений составляющих его цифр на соответствующие степени основания системы:

Примеры:

1. Десятичная с/с

      Разряды  2  1    0

          3 0 8 = 8 * 10⁰ + 0 * 10¹ + 3 * 10²

 

2. Двоичная с/с

     Разряды    4  3  2   1  0

             1 1 1 0 1₂ = 1* 2 ⁰+ 0* 2 ¹+1* 2 ²+1* 2 ³+1* 2 ⁴ = 1 + 0 + 4 + 8 + 16 = 29 ₁₀

Таким образом, из исходного двоичного числа получили десятичное число.

                          Перевод двоичных чисел в десятичные   

 

Как перевести двоичное число в десятичное?

Двоичное число надо представить в виде суммы произведений составляющих его цифр на соответствующие степени числа 2, а затем вычислить полученную сумму.

           Степени числа 2:

2 ⁰ =1  2¹=2      2²=4          2³=8            2⁴=16             2⁵ =32

2⁶=64    2⁷=128  2⁸=256      2⁹=512        2¹⁰=1024

 

Упражнения: Перевести двоичные числа 1) 1011;  2) 10011010 в десятичные.

Решение:

    3    2 1  0

1)  1 0 1 1₂ = 1* 2 ⁰+ 1* 2 ¹+ 0* 2 ²+1* 2 ³ = 1 + 2 + 0 + 8 = 11₁₀     Ответ: 11

       7  6   5  4  3  2   1  0

2)   1 0 0 1 1 0 1 0₂  = 0* 2 ⁰+ 1* 2 ¹+0* 2 ²+1* 2 ³+1* 2 ⁴+0* 2 ⁵+0* 2 ⁶+1* 2 ⁷= 0 + 2 + 0 + 8 + 16 + 0 + 0 + 128 = 154₁₀                                                  Ответ: 154

 

Соответствие чисел в системах счисления

 

Десятичные	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Двоичные	0	1	10	11	100	…			1000	…							10000

Перевод десятичных чисел в двоичные

 

Как перевести десятичное число в двоичное?

Десятичное число надо последовательно делить нацело на 2, а затем выписать справа налево результат из остатков деления, начиная с последнего частного.

 

Пример:

Перевести десятичное число 13 в двоичное.

                     13  2

                       12  6 2                                                                                Ответ: 1101

              1 6 3 2           

                    0 2    1

                             1

 

 

Можно сделать проверку:

3  2  1  0

1 1 0 1₂ = 1* 2 ⁰+ 0* 2 ¹+ 1* 2 ²+1* 2 ³ = 1 + 0 + 4 + 8 = 13₁₀

Упражнения:

1. Переведите число 1010110 из двоичной системы в десятичную.

2. Переведите число 124 из десятичной системы в двоичную.

Компьютер пользуется очень простыми правилами сложения и умножения:

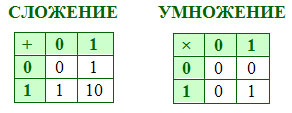
Степени числа 2:

Несколько арифметических примеров в двоичной системе счисления:
1) Сложить числа 111₂ и 1₂.

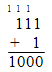
Проверка:
111₂ = 1×2⁰ + 1×2¹ + 1×2² = 7₁₀
1₂ = 1×2⁰ = 1₁₀
1000₂ = 0×2⁰ + 0×2¹ + 0×2² + 1×2³ = 8₁₀
7 + 1 = 8

1) Вычесть из числа 1101₂ число 11₂.

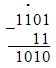
Проверка:
1101₂ = 1×2⁰ + 0×2¹ +1×2² + 1×2³ = 13₁₀
11₂ = 1×2⁰ + 1×2¹ = 3₁₀
1010₂ = 0×2⁰ + 1×2¹ + 0×2² + 1×2³ = 10₁₀
13 - 3 = 10

2) Умножить числа 101₂ и 110₂.

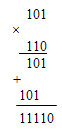
Проверка:
101₂ = 1×2⁰ + 1×2² = 5₁₀
110₂ = 1×2¹ + 1×2² = 6₁₀
11110₂ = 1×2¹ + 1×2² + 1×2³ + 1×2⁴ = 30₁₀
6 × 5 = 30

Основанием позиционной системы счисления может быть любое натуральное число.

Например, вы можете работать в шестеричной системе, тогда в ней должно быть 6 цифр (символов алфавита): 0, 1, 2, 3, 4, 5.

Чтобы перевести какое-нибудь число (например, 235) из этой системы в десятичную, нам нужно разложить его по степеням шестерки (основания системы): 235₆ = 5×6⁰ + 3×6¹ +2×6² = 5 + 18 + 72 = 95₁₀ А чтобы перевести число из десятичной системы в шестеричную, нужно делить это число на 6 (на основание системы счисления) с остатками:

95: 6 = 15 (5)
15: 6 = 2 (3)
95₁₀ = 235₆

Аналогично и в любых других системах счисления. В программировании часто используются восьмеричная и шестнадцатеричная системы счисления. Рассмотрим их подробнее.

 

В восьмеричной системе должно быть 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7.

Переведем, например, число 137 из восьмеричной системы в десятичную:

137₈ = 7×8⁰ + 3×8¹ + 1×8² = 7 + 24 + 64 = 95₁₀

Теперь наоборот, число 76 из десятичной системы в восьмеричную:

76: 8 = 9 (4)
9: 8 = 1 (1)
76₁₀ = 114₈

А можно ли перейти из восьмеричной системы в двоичную? Казалось бы придется переходить сначала из восьмеричной в десятичную, а потом уже из десятичной в двоичную. Но оказывается есть более простой способ. Сначала каждое число, соответствующее цифре восьмеричной системы, представим в виде трехразрядного двоичного кода (переведем в двоичную систему).

Чтобы перевести число из восьмеричной системы в двоичную, надо каждую его цифру заменить на соответствующую тройку цифр (двоичный код).

Например, переведем восьмеричное число 351 в двоичное:
351₈= 011 101 001 = 11101001₂

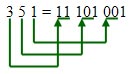Для перевода двоичного числа в восьмеричное надо наоборот, разбить исходное число на тройки цифр, начиная с конца, и заменить каждую тройку на соответствующую ей цифру восьмеричной системы.

Например, переведем двоичное число 11100110 в восьмеричное:
                           11100110₂ = 011 100 110 = 346₈

 

Теперь рассмотрим шестнадцатеричную систему счисления. В ней должно быть 16 цифр. Обозначение первых десяти можно взять из десятичной системы счисления, а для остальных шести решили использовать первые шесть букв латинского алфавита: 10 - A, 11 - B, 12 - C, 13 - D, 14 - E, 15 - F.

 

Переведём число А1F8 из шестнадцатеричной системы в десятичную:

А1F8₁₆ = 8×16⁰ + 15×16¹ + 1×16² + 10×16³ = 8 + 240 + 256 + 40960 = 41464₁₀

В обратную сторону: число 196 из десятичной системы в шестнадцатеричную:
                   196: 16 = 12 (4),  

      т.е. 196₁₀ = С4₁₆

А есть ли простая связь между числами двоичной и шестнадцатеричной систем? Оказывается, есть и аналогична связи между числами двоичной и восьмеричной систем.

Опять запишем каждое число, соответствующее цифре шестнадцатеричной системы в виде двоичного кода, только теперь четырехразрядного.
Теперь для перевода числа из шестнадцатеричной системы в двоичную надо каждую его цифру заменить на соответствующую четверку двоичных цифр.

Для перевода двоичного числа в шестнадцатеричную систему счисления надо наоборот, разбить исходное число на группы из четырех цифр, начиная с конца, и заменить каждую четверку на соответствующую ей цифру шестнадцатеричной  системы.

Примеры. Перевести число 5А1 из шестнадцатеричной системы в двоичную:

5А1₁₆ = 0101 1010 0001 = 10110100001₂

 

Перевести число 1101101 из двоичной системы в шестнадцатеричную:

1101101₂ = 0110 1101 = 6D₁₆

    Контрольные вопросы:

1. В чем заключаются достоинства двоичного кодирования информации?

2. Как кодируются тексты?

3. Как кодируются изображения?

4. На чем основано кодирование числовой информации для компьютера?

5. Дать определение системы счисления, основания системы счисления.

6. Сформулировать правило перевода чисел, записанных в десятичной системе счисления  

a) в двоичную систему счисления,

b) восьмеричную систему счисления,

c) шестнадцатеричную систему счисления.

7. Сформулировать правило перевода чисел, записанных в 2-й, 8-й, 16-й системе счисления в десятичную систему счисления.

8. Сформулировать правило перевода чисел из двоичной системы счисления в восьмеричную систему счисления и наоборот.

9. Сформулировать правило перевода чисел из двоичной системы счисления в шестнадцатеричную систему счисления и наоборот.