Наблюдение и измерение цифровых изображений

 

Как уже отмечалось выше, цифровое изображение хранится в памяти компьютера, в общем случае, в виде прямоугольной матрицы, элементы  которой несут информацию об оптических плотностях или цвете элементарных участков изображения, а номера i строки и j столбца элемента  определяют его положение в матрице. Нумерация строк и столбцов матрицы цифрового изображения начинается с нуля.

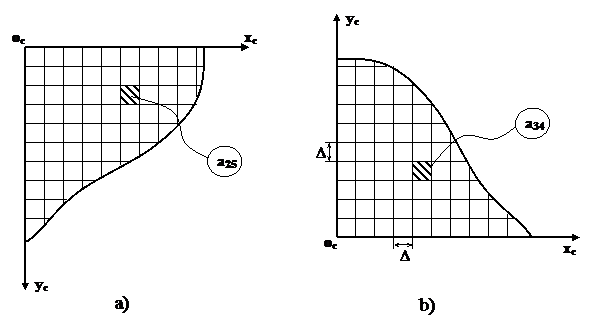
Рис.1.1

Различают две прямоугольных системы координат цифрового изображения: левую о _C x_C у _C (рис.1.1a), началом которой является левый верхний угол цифрового изображения и правую - о _C x_C у _C (рис.1.1b), началом которой является пиксель, расположенный в левом нижнем углу цифрового изображения. Ось x совпадает с соответствующей строкой, а ось y – со столбцом матрицы цифрового изображения.

       Левая система координат принята при записи изображений в файл во всех форматах и используется в большинстве программ по обработке изображений. В фотограмметрии традиционно применяется правая система координат для анализа снимка, и многие современные цифровые фотограмметрические системы используют именно эту систему координат. Поэтому в дальнейшем будем использовать в качестве системы координат цифрового изображения правую прямоугольную систему координат о _C x_C у _C (рис.1.1b). В этой системе координат координаты любой точки определяются в, так называемых, пиксельных координатах (единицей измерения в этом случае является пиксель).

       Пиксельные координаты центров пикселей в системе координат цифрового изображения о _C х _C у _C определяют по формулам: 

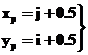                            .                                       (1.1)           

Для измерения координат точек цифрового изображения его визуализируют на экране дисплея. Если пиксель изображения на экране дисплея соответствует пикселю исходного цифрового изображения, то с помощью “мыши” или клавиатуры компьютера можно навести измерительную марку, формируемую в виде цифрового изображения на экране дисплея, на точку изображения с точностью до одного пикселя.

Для получения подпиксельной (субпиксельной) точности можно увеличить матрицу изображения на экране монитора относительно исходного цифрового изображения. В этом случае каждый пиксель исходного изображения будет изображаться матрицей n × n пикселей, численное значение всех элементов a ' _ij которой будут равны численному значению элемента матрицы исходного изображения.

Пиксельные координаты точек увеличенного изображения можно измерить с точностью до 1/ n пикселя исходного изображения (рис.1.2.).

Рис. 1.2

Пиксельные координаты (в пикселях исходного изображения) элемента a ' _ij увеличенного изображения определяют по формуле:

 ,                                 (1.2)

в которых: i, j - номера строки и столбца элемента матрицы исходного изображения, в котором находится элемент a ' _ij увеличенного изображения:

         i ’, j ’ - номера строки и столбца элемента a ` _ij подматрицы n × n;

         n – коэффициент увеличения изображения.

Например, для элемента a ’₂₃ (рис.1.2) пиксельные координаты:

Значения физических координат центров пикселей цифрового изображения можно определить по значениям их пиксельных координат, если известны физические размеры стороны пикселя изображения Δ (предполагается, что пиксель имеет форму квадрата).

Значения физических координат определяют по формулам:

.                                         (1.3)

Например, координаты центра пикселя, соответствующего элементу a ’₂₃ (рис.1.2) при величине Δ =20 мкм будут равны х _c = 34 мкм и y_c = 50 мкм.

В некоторых цифровых системах начало системы координат цифрового изображения о _c х _c у _c выбирают в центре пикселя, расположенного в нижнем левом углу цифрового изображения (рис.1.3).

                  

Рис.1.3

В этом случае значения пиксельных координат вычисляют по формулам:

                    ,                                             (1.4)

при измерениях с точностью до пикселя и по формулам:

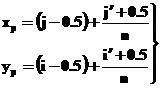                                 ,                          (1.5)

при измерениях с подпиксельной точностью.

Например, для того же элемента a ’₂₃ (рис.1.3) пиксельные координаты равны:

 Рассмотренный выше метод измерения цифрового изображения с подпиксельной точностью требует его увеличения на экране дисплея компьютера. Однако, даже при увеличении цифрового изображения только в два раза, на экране дисплея исходный аналоговый снимок изображается с весьма значительным оптическим увеличением. Так, например, снимок, преобразованный на сканере, с размером пикселя 14 мкм на экране дисплея с размером зерна 0.28 мм при увеличении цифрового изображения снимка в 2 раза имеет оптическое увеличение 40 раз. Такое увеличение приводит к значительному ухудшению изобразительных свойств наблюдаемого изображения и, как следствие, к снижению точности наведения измерительной марки на измеряемые объекты на изображении.

С целью обеспечения возможности измерения координат точек цифрового изображения с подпиксельной точностью без увеличения исходного изображения разработан метод измерения цифровых изображений, в котором цифровое изображение снимка может смещаться относительно неподвижной измерительной марки с шагом в n – раз меньшим размера пикселя.

Принцип измерения координат точек цифрового изображения по этому методу иллюстрируется на рис.1.4.

Рис. 1.4

 

На рис.1.4а представлен фрагмент исходного цифрового изображения с измерительной маркой (в виде креста) и точкой изображения m, координаты которой необходимо измерить. Как следует из этого рисунка, центр изображения измерительной марки не совпадает с изображением точки m, причем разности значений их пиксельных координат составляют величины D x _P и D y _P.

Для совмещения центра изображения измерительной марки с точкой m можно создать фрагмент цифрового изображения снимка, в котором координаты начала системы координат o ’_с x ’_с y ’_с будут иметь значения 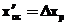, а .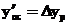

Создание такого фрагмента цифрового изображения производится следующим образом. По координатам центра каждого пикселя фрагмента изображения x ’ _pi, y ’ _pi определяют значения координат его проекции x_pi, y_pi в системе координат о_с х_с у_с исходного изображения.

Их значения определяют по формулам:

 .                                 (1.6)

Затем по значениям координат x_pi, y_pi находят ближайшие к изображению точки i, соответствующей центру пикселя

                             

Рис. 1.5

создаваемого фрагмента цифрового изображения, четыре пикселя исходного цифрового изображения, например, M, K, L, N (рис.1.5)

Далее методом билинейного интерполирования определяют значения оптической плотности i -го пикселя создаваемого фрагмента изображения по формуле:

 ,                     (1.7)

в которой

 .

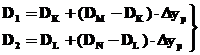Таким же образом формируются все элементы (пиксели) создаваемого фрагмента цифрового изображения.

На экране дисплея, на визуализированном фрагменте созданного цифрового изображения центр измерительной марки будет совмещен с изображением точки m. Пиксельные координаты точки m изображения в системе координат исходного изображения определяются по формулам 1.6.

Необходимо отметить, что создание фрагмента цифрового изображения требует значительных вычислительных процедур. Поэтому для достижения эффекта перемещения изображения на экране дисплея относительно марки в “реальном масштабе” времени фрагмент изображения не должен иметь большие размеры.

В случае если для измерений используются цветные цифровые изображения при формировании элементов создаваемого изображения методом билинейного трансформирования по формулам (1.7) определяются интенсивности красного (R), зеленого (G) и синего (В) компонентов цветного изображения.

 1.3. Внутреннее ориентирование снимка

       

       В фотограмметрии различают два понятия: элементы внутреннего ориентирования снимка и внутреннее ориентирование снимка. Элементы внутреннего ориентирования снимка позволяют восстановить связку проектирующих лучей, сформировавших снимок, в системе координат снимка o ’ xyz. Для этого, (как уже отмечалось) согласно формуле (1.1.1), необходимо знать: эти элементы f, x _о, y _о и координаты x, y, измеренные в системе координат снимка o ’ xyz. На практике измерения координат точек снимка осуществляется в некоторой измерительной системе координат , связанной с измерительным прибором. Поэтому существует еще процесс «внутреннее ориентирование снимка».

В процессе внутреннего ориентирования снимка определяют параметры перехода из измерительной системы координат  в систему координат снимка o ’ xyz (рис. 1.6). Другими словами, определяют параметры внутреннего ориентирования снимка – величины, характеризующие положение и ориентацию системы координат снимка в измерительной системе координат, а также параметры, характеризующие влияние систематических ошибок, вызванных деформацией фотоматериала, на котором был получен исходный аналоговый снимок.

                    

Рис.1.6

 

В качестве измерительного прибора в фотограмметрии используются стреокомпараторы, аналитические и цифровые фотограмметрические системы. Назначение и устройство этих приборов и систем будет рассмотрено позже. Рассмотрим процесс внутреннего ориентирования снимка, для случая, когда аналоговый снимок преобразуется в цифровую форму с помощью сканера для дальнейшей обработки на цифровой фотограмметрической системе. В этом случае измерительная система координат  совпадает с системой координат цифрового изображения o_cx_cy_c (рис.1.6). Здесь, o ’ xy – система координат снимка, а 1,2,3,4 – координатные метки.

Для определения параметров внутреннего ориентирования снимка измеряют координаты изображений координатных меток снимка в измерительной системе координат .

Возможны три варианта внутреннего ориентирования снимка в зависимости от того, что определялось в процессе фотограмметрической калибровки съемочной камеры.

1. В результате фотограмметрической калибровки камеры были определены координаты координатных меток в системе координат снимка o ’ xy.

2. В результате фотограмметрической калибровки камеры были определены расстояния между координатными метками.

3. Информация о координатных метках отсутствует.

Рассмотрим каждый из этих вариантов.

 

1) Если в результате фотограмметрической калибровки съемочной камеры были определены координаты координатных меток в системе координат съемочной камеры (снимка), то для определения координат точек в системе координат снимка по значениям их координат в системе цифрового изображения используют формулы аффинного преобразования координат:

                                                                                                       ,          (1.8)

 

или в развернутом виде:

        .                                         (1.9)

 

Здесь, a_o, a ₁, a ₂, b_o, b ₁, b ₂ – параметры аффинных преобразований; a_o, b_o – координаты начала системы координат снимка в измерительной системе координат, a ₁, a ₂, b ₁, b ₂ – параметры, характеризующие ориентацию системы координат снимка в измерительной системе координат, разномасштабность (деформация фотоматериала) вдоль осей системы координат снимка и их неперпендикулярность. 

Таким образом, формулы (1.8) позволяют не только определить положение и ориентацию системы координат снимка в системе координат цифрового изображения, но и учесть систематические искажения снимка, возникающие из-за деформации фотопленки, на которой был получен снимок.

Параметры аффинного преобразования a_i, b_i можно определить по координатам координатных меток снимка, измеренных на цифровом изображении, и значениям координат x, y этих меток в системе координат снимка, полученным при калибровке съемочной камеры.

Для определения параметров a_i, b_i для каждой метки, измеренной на цифровом изображении, составляют уравнения:

 .                    (1.10)

Полученную систему уравнений решают по методу наименьших квадратов и определяют в результате решения значения параметров a_i, b_i. Для их определения необходимо не менее 3 координатных меток, не лежащих на одной прямой.

В практике фотограмметрии возникает обратная задача: определение значений координат точек в измерительной системе координат по координатам этих точек, заданным в системе координат снимка. Такое преобразование координат выполняется по формулам:

    (1.11)

или

.                 (1.12)

В формулах (1.11) и (1.12) A_i, B_i – элементы обратной матрицы Р^-1.

Для цифровых изображений значение пиксельных координат точек x_p, y_p определяют по формулам:

 .                                           (1.13)

 

2) В случае, если при калибровке съемочной камеры определялись калиброванные расстояния между координатными метками L_x, L_y (рис.1.7), для определения координат                                   

Рис.1.7

точек в системе координат снимка по измеренным координатам точек в измерительной системе координат используют формулы ортогональных преобразований:

                                                               (1.14)

Здесь a _о, b _о – координаты начала системы координат снимка o ’ в измерительной системе координат ; параметры a ₁, a ₂ определяют разворот одной системы координат относительно другой(a ₁ = cos φ, a ₂ = sin φ); φ – угол поворота (рис.1.7); k_x, k_y – коэффициенты деформации снимка по осям x и y.

       Параметры внутреннего ориентирования a _о, b _о, φ, k_x, k_y определяют по измерениям координат координатных меток. Параметры a _о, b _о вычисляют как координаты точки пересечения прямых линий, проведенных через координатные метки 1-2 и 3-4 по формулам:

 

                                             (1.15)

где

 

Значение угла φ определяют по формуле:

 

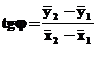                                                                            (1.16)

Коэффициенты деформации снимка вычисляют по формулам:

                                                  (1.17)

в которых

L_x, L_y – калиброванные значения расстояний между координатными метками (рис.1.7).

L ’ _x, L ’ _y - вычисленные значения расстояний между соответственными координатными метками, на основе измеренных координат этих меток.

 

Для обратного перехода из системы координат снимка в измерительную систему координат используют формулы:

                                                                                                  (1.18)

 

       3) Информация (координаты или расстояния) о координатных метках отсутствует. В этом случае внутреннее ориентирование снимка выполняется по формулам (1.14), полагая в них k_x = k_y = 1, т.е. применяются ортогональные преобразования системы координат (перенос и разворот) без учета деформации снимка. При этом обратные преобразования выполняются по формулам:

 

                                                                              (1.19)

       Полученные после внутреннего ориентирования снимка координаты x, y любой точки снимка используют для дальнейшей фотограмметрической обработки с целью получения координат соответствующих точек объекта.

Примечание.  

 

1) В случае если съемка выполнялась с помощью цифровой камеры, то внутреннее ориентирование снимка не выполняется, так как измерения координат точек снимка выполняются непосредственно в системе координат снимка (рис.1.8).

 

 

                                         

           

Рис 1.8

 

2) В случае, если координаты точек аналогового снимка (рис.1.9) измеряются на оптико-механическом приборе (монокомпаратор, стереокомпаратор, аналитическая система), то внутреннее ориентирование выполняется аналогично, тому как это делалось для цифрового изображения, т.е по формулам (1.8 - 1.18).

                                                                              

 

Рис. 1.9