Плоскость и прямая в пространстве
Уравнением поверхности в пространстве Oxyz называется уравнение F (x, y, z)=0, которое обращают в верное равенство координаты всех точек данной поверхности, и которому не удовлетворяют точки вне данной поверхности.
Уравнение плоскости в пространстве
Уравнение плоскости, проходящей через три заданные точки
Для того, чтобы три точки пространства M 1(x 1; y 1; z 1); M 2(x 2; y 2; z 2); M 3(x 3; y 3; z 3), определяли плоскость 
, они не должны лежать на одной прямой. Поскольку точки лежат в одной плоскости, то для произвольной точки M (x; y; z) из этой плоскости векторы
={ x – x 1; y – y 1; z – z 1}, 
={ x 2– x 1; y 2– y 1; z 2– z 1} и 
={ x 3– x 1; y 3– y 1; z 3– z 1} будут компланарны, а их смешанное произведение равно нулю. Смешанное произведение в координатной форме имеет вид
. (1)
Это равенство и определяет уравнение плоскости , проходящей через три заданные точки.
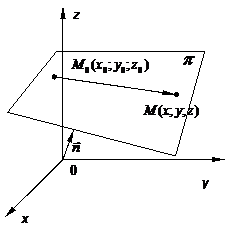2 Уравнение плоскости с нормальным вектором
Пусть плоскость проходит через точку M 0(x 0; y 0; z 0) перпендикулярно вектору 
=(A; B; C). Этими условиями определяется единственная плоскость в пространстве Oxyz. Вектор называется нормальным вектором плоскости .
Для произвольной точки M (x; y; z) из плоскости вектор 
={ x – x 0; y – y 0; z – z 0} будет перпендикулярен вектору =(A; B; C), а скалярное произведение этих векторов равно нулю, т.е. 
=0. В координатной форме последнее равенство имеет вид
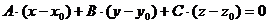. (2)
Уравнение (2) представляет уравнение плоскости, перпендикулярной данному вектору =( A; B; C ) и проходящей через данную точку M 0 ( x 0; y 0; z 0).
Уравнение плоскости в отрезках
Пусть плоскость пересекает ось O x в точке A (a; 0; 0), ось Oy в точке B (0; b; 0), а ось Oz в точке C (0; 0; c). Тогда уравнение плоскости в отрезках (каноническое уравнение плоскости) имеет вид
. (3)
Общее уравнение плоскости
Уравнение плоскости (2), записанное в виде
, (4)
где 
, называется общим уравнением плоскости.
При различных сочетаниях значений коэффициентов получаются различные плоскости.
1) A =0; B 
0; C 0; D 0 – уравнение плоскости, параллельной оси Ox.
2) A 0; B =0; C 0; D 0 – уравнение плоскости, параллельной оси O y.
3) A 0; B 0; C =0; D 0 – уравнение плоскости, параллельной оси O z.
4) A 0; B 0; C 0; D =0 – уравнение плоскости, проходящей через начало координат.
5) A= B=0; C 0; D 0 – уравнение плоскости, параллельной плоскости Ox y.
6) A= C =0; B 0; D 0 – уравнение плоскости, параллельной плоскости Ox z.
7) A 0; B = C =0; D 0 – уравнение плоскости, параллельной плоскости O yz.
8) A= D =0; B 0; C 0 – уравнение плоскости, проходящей через ось Ox.
9) A 0; B = D =0; C 0 – уравнение плоскости, проходящей через ось O y.
10) A 0; B 0; C = D =0– уравнение плоскости, проходящей через ось O z.
11) A = B = D =0; C 0 – уравнение плоскости Ox y.
12) A = C = D =0; B 0 – уравнение плоскости Ox z.
13) A 0; B = C = D =0 – уравнение плоскости O yz.
Условия параллельности и перпендикулярности плоскостей
Пусть две плоскости 
и 
заданы своими общими уравнениями 
и 
. Их нормальные вектора определяются как 
=(A 1; B 1; C 1) и 
=(A 2; B 2; C 2).
Две плоскости параллельны, если параллельны их нормальные вектора. В этом случае их координаты пропорциональны, т.е. 
.
Две плоскости перпендикулярны, если перпендикулярны их нормальные вектора. В этом случае их скалярное произведение равно нулю, т.е.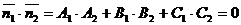 
.
Угол между плоскостями
Под углом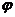 
между плоскостями и , заданными своими общими уравнениями и , понимают угол между их нормальными векторами =(A 1; B 1; C 1) и =(A 2; B 2; C 2). Тогда 
.
