а) Если прямые  и
и 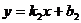 параллельны, то угол между ними
параллельны, то угол между ними 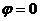 ,
,  , откуда
, откуда 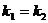 .
.
б) Если прямые, заданные общими уравнениями 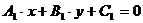 и
и 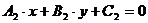 , параллельны, то их нормальные вектора
, параллельны, то их нормальные вектора  и
и 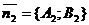 также параллельны, а их координаты пропорциональны. Тогда условие параллельности прямых, заданных общими уравнениями, формулируется как
также параллельны, а их координаты пропорциональны. Тогда условие параллельности прямых, заданных общими уравнениями, формулируется как 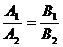 .
.
в) Если прямые  и
и 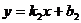 перпендикулярны, то угол между ними
перпендикулярны, то угол между ними  ,
, 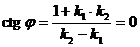 , откуда
, откуда 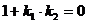 и
и  .
.
г) Если прямые, заданные общими уравнениями 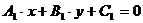 и
и 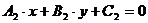 , перпендикулярны, то их нормальные вектора
, перпендикулярны, то их нормальные вектора  и
и 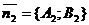 также перпендикулярны, а их скалярное произведение равно нулю. Тогда условие перпендикулярности прямых, заданных общими уравнениями, формулируется как
также перпендикулярны, а их скалярное произведение равно нулю. Тогда условие перпендикулярности прямых, заданных общими уравнениями, формулируется как 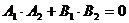 .
.
11 Точка пересечения прямых.
Пусть даны две прямые 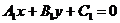 и
и 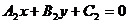 . Очевидно, что координаты их точки пересечения должны удовлетворять уравнению каждой прямой, т.е. они могут быть найдены из системы
. Очевидно, что координаты их точки пересечения должны удовлетворять уравнению каждой прямой, т.е. они могут быть найдены из системы
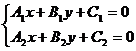 .
.
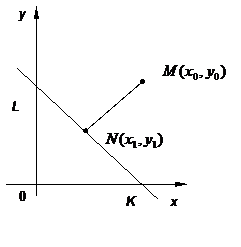 Если прямые не параллельны, т.е.
Если прямые не параллельны, т.е.  , то решение системы дает единственную точку пересечения прямых.
, то решение системы дает единственную точку пересечения прямых.
12 Расстояние от точки до прямой.
Пусть даны точка  и прямая
и прямая 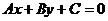 . Под расстоянием от точки
. Под расстоянием от точки 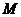 до прямой
до прямой 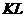 понимается длина перпендикуляра
понимается длина перпендикуляра 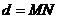 , опущенного из точки
, опущенного из точки 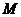 на прямую
на прямую 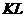 . Можно показать, что его величина определяется по формуле
. Можно показать, что его величина определяется по формуле 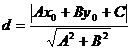 .
.
Кривые второго порядка на плоскости
Окружность
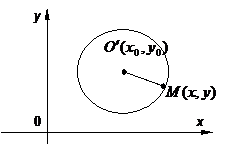 Уравнение окружности радиуса
Уравнение окружности радиуса 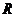 с центром
с центром  имеет вид
имеет вид
 . (9)
. (9)
В частности, уравнение окружности с центром в начале координат 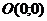 имеет вид
имеет вид  .
.
Рассмотрим уравнение второй степени с двумя переменными в общем виде
 , (10)
, (10)
в котором  ,
, 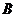 и
и 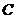 не равны нулю одновременно, т.е.
не равны нулю одновременно, т.е. 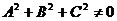 .
.
Чтобы уравнения (9) и (10) представляют одну и ту же линию, коэффициент 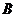 должен равняться нулю, т.е.
должен равняться нулю, т.е. 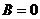 , а все остальные коэффициенты – быть пропорциональны, в частности,
, а все остальные коэффициенты – быть пропорциональны, в частности, 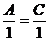 , откуда
, откуда 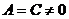 (т.к.
(т.к. 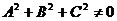 , а
, а 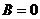 ). Тогда получим уравнение
). Тогда получим уравнение
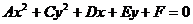 , (11)
, (11)
называемое общим уравнением окружности.
Поделив обе части уравнения на 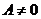 и дополнив члены, содержащие
и дополнив члены, содержащие 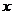 и
и 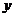 , до полного квадрата, получим
, до полного квадрата, получим
 . (12)
. (12)
Сравнивая уравнения (12) и (9), можно сделать вывод что уравнение (12) есть уравнение действительной окружности, если 1)  ; 2)
; 2) 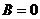 ; 3)
; 3) 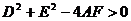 . При выполнении этих условий центр окружности (12) расположен в точке
. При выполнении этих условий центр окружности (12) расположен в точке 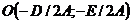 , а ее радиус
, а ее радиус 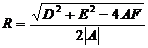 .
.
Эллипс
Перепишем (10) в виде  или
или 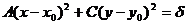 , где
, где 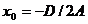 ;
; 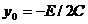 ;
;  . В предположении
. В предположении  уравнение кривой примет вид:
уравнение кривой примет вид:
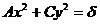 . (13)
. (13)
Кривая второго порядка (13) называется эллипсом (кривой эллиптического типа), если коэффициенты  и
и 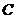 имеют одинаковые знаки. Будем считать, что
имеют одинаковые знаки. Будем считать, что 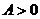 и
и 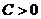 (в противном случае обе части уравнения можно умножить на (
(в противном случае обе части уравнения можно умножить на (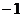 )). Тогда возможны три случая:
)). Тогда возможны три случая:
1) 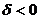 – кривая (13) не имеет действительных точек;
– кривая (13) не имеет действительных точек;
2) 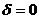 – кривая (13) представляет собой одну точку;
– кривая (13) представляет собой одну точку;
3) 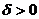 – кривая (13) переписывается в виде
– кривая (13) переписывается в виде
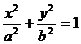 . (14)
. (14)
 Уравнение (14) называется каноническим уравнением эллипса с полуосями
Уравнение (14) называется каноническим уравнением эллипса с полуосями  и
и  . При
. При 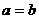 уравнение (14) представляет собой уравнение окружности
уравнение (14) представляет собой уравнение окружности 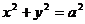 . В предположении, что a > b, обозначим
. В предположении, что a > b, обозначим  , тогда точки
, тогда точки 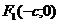 и
и  называются фокусами эллипса, а отношение
называются фокусами эллипса, а отношение  – его эксцентриситетом. Эксцентриситет характеризует форму эллипса. Очевидно, что
– его эксцентриситетом. Эксцентриситет характеризует форму эллипса. Очевидно, что  , причем для окружности
, причем для окружности 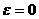 .
.
Можно показать, что для любой точки эллипса сумма расстояний от этой точки до фокусов есть величина постоянная, равная 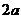 . Это характеристической свойство эллипса часто принимается за его определение.
. Это характеристической свойство эллипса часто принимается за его определение.
Гипербола
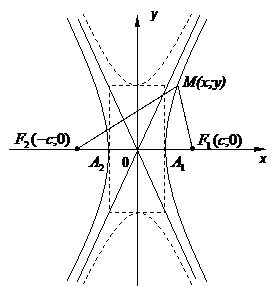 Кривая второго порядка (13) называется гиперболой (кривой гиперболического типа), если коэффициенты
Кривая второго порядка (13) называется гиперболой (кривой гиперболического типа), если коэффициенты  и
и 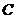 имеют противоположные знаки, т.е.
имеют противоположные знаки, т.е. 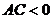 . Пусть для определенности
. Пусть для определенности 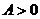 ,
, 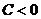 . Возможны три случая.
. Возможны три случая.
1) 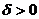 соответствует гиперболе с каноническим уравнением вида
соответствует гиперболе с каноническим уравнением вида
 , (15)
, (15)
где  – действительная полуось, а
– действительная полуось, а 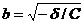 – мнимая полуось. Фокусы гиперболы – точки
– мнимая полуось. Фокусы гиперболы – точки  и
и 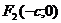 , где
, где  , а ее эксцентриситет
, а ее эксцентриситет  принимает любые значения, большие единицы. Вершины гиперболы – точки
принимает любые значения, большие единицы. Вершины гиперболы – точки  и
и  . Можно показать, что для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов есть величина постоянная, равная
. Можно показать, что для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов есть величина постоянная, равная 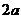 :
: 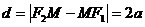 . Это характеристическое свойство гиперболы часто принимают за определение гиперболы. Прямые
. Это характеристическое свойство гиперболы часто принимают за определение гиперболы. Прямые  , называется асимптотами гиперболы. Для равносторонней гиперболы (
, называется асимптотами гиперболы. Для равносторонней гиперболы (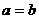 )
) 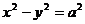 асимптоты
асимптоты 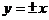 взаимно перпендикулярны и представляют биссектрисы координатных углов.
взаимно перпендикулярны и представляют биссектрисы координатных углов.
2) При 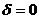 уравнение кривой (15) примет вид
уравнение кривой (15) примет вид  , т.е. получим пару пересекающихся прямых
, т.е. получим пару пересекающихся прямых 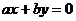 и
и  .
.
3) При 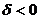 получим гиперболу
получим гиперболу  с полуосями
с полуосями 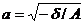 - и
- и  , называемую сопряженной с гиперболой (15) (на рисунке она изображена пунктиром).
, называемую сопряженной с гиперболой (15) (на рисунке она изображена пунктиром).
Парабола
Пусть в уравнении кривой второго порядка (10) 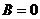 , а также один из коэффициентов
, а также один из коэффициентов  или
или 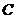 равен нулю. Пусть для определенности
равен нулю. Пусть для определенности  ,
, 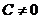 ,
, 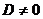 тогда
тогда
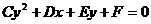 . (16)
. (16)
Или, после выделения полного квадрата при y:  .
.
Полагая 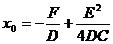 ,
, 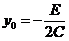 ,
,  , получим
, получим
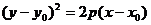 . (17)
. (17)
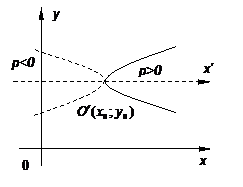 Кривая (17) называется параболой, точка
Кривая (17) называется параболой, точка  – вершиной параболы, p – параметром параболы. При
– вершиной параболы, p – параметром параболы. При 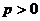 ветви параболы направлены вправо, при
ветви параболы направлены вправо, при 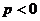 - влево. Прямая
- влево. Прямая 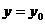 является осью симметрии параболы.
является осью симметрии параболы.
Если вершина параболы находится в начале координат, то уравнение (17) принимает вид:
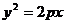 . (18)
. (18)
Точка 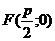 называется фокусом параболы, а прямая
называется фокусом параболы, а прямая  - ее директрисой.
- ее директрисой.
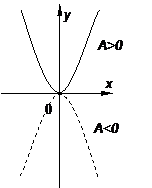 Можно показать, что парабола представляет множество всех точек плоскости, равноотстоящих от данной точки (фокуса) и от данной прямой (директрисы). Это характеристической свойство параболы часто принимается за определение параболы.
Можно показать, что парабола представляет множество всех точек плоскости, равноотстоящих от данной точки (фокуса) и от данной прямой (директрисы). Это характеристической свойство параболы часто принимается за определение параболы.
Если в уравнении (18) поменять местами 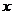 и
и 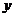 , то получим
, то получим  - уравнение параболы с вершиной в начале координат, симметричной относительно оси ординат. Это уравнение обычно записывают в виде
- уравнение параболы с вершиной в начале координат, симметричной относительно оси ординат. Это уравнение обычно записывают в виде 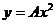 , где
, где  . При
. При 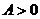 ветви параболы направлены вверх, при
ветви параболы направлены вверх, при  - вниз.
- вниз.
Можно показать, что, график квадратного трехчлена 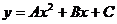 есть парабола с вершиной в точке
есть парабола с вершиной в точке 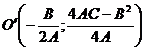 и осью симметрии
и осью симметрии  , параллельной оси
, параллельной оси 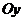 .
.






