n -мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде 
, где 
- i -я компонента вектора 
Два n -мерных вектора равны если равны их соответствующие компоненты, т.е. 
, если 
.
Суммой двух векторов одинаковой размерности n называется вектор 
, компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е. 
, .
Произведением вектора на действительное число 
называется вектор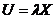 
, компоненты 
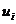которого равны произведению на соответствующие компоненты вектора , т.е. 
.
Линейные операции над векторами обладают следующим свойствам:
1) 
– коммутативность сложения векторов;
2) 
– ассоциативность сложения векторов;
3) 
– ассоциативность умножения вектора на число;
4) 
– дистрибутивность умножения на число суммы векторов;
5) 
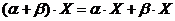– дистрибутивность умножения вектора на сумму чисел;
6) Существует нулевой вектор 
такой, что 
для любого вектора ;
7) Для любого вектора существует противоположный вектор 
такой, что 
;
8) 
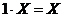для любого вектора .
Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным выше восьми свойствам (рассматриваемым как аксиомы), называется линейным (векторным) пространством.
Вектор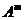 
называется линейной комбинацией векторов 
векторного пространства R, если он равен сумме произведений этих векторов на произвольные действительные числа: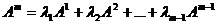 
, где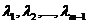 
– какие угодно действительные числа.
Векторы 
векторного пространства R называются линейно зависимыми, если существуют такие числа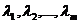 
, не равные одновременно нулю, что 
. В противном случае векторы называются линейно независимыми.
Векторы линейного пространства обладают следующими свойствами:
1) если среди векторов имеется нулевой вектор, то эти векторы линейно зависимы;
2) Если часть векторов являются линейно зависимыми, то и все эти векторы – линейно зависимые.
Линейное пространство R называется n -мерным, если в нем существует n линейно независимых векторов, а любые из 
векторов являются зависимыми. Число n называется размерностью пространства R и обозначается dim (R). Другими словами, размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов.
Совокупность n линейно независимых векторов n -мерного пространства R называется базисом. Его обозначают 
. Справедлива следующая теорема.
Теорема. Каждый вектор линейного пространства R можно представить и притом единственным способом в виде линейной комбинации векторов базиса вида 
.
Выражение называют разложением вектора по базису , а числа 
- координатами вектора относительно этого базиса. В силу единственности разложения каждый вектор однозначно может быть определен координатами в некотором базисе.
Базис векторного пространства обладает следующими свойствами:
1) базис не единственен;
2) все базисы n -мерного пространства состоят из одного и того же числа векторов n;
3) всякая система из (n +1)-го вектора n -мерного пространства линейно зависима.
Поскольку базис векторного пространства не единственен, возникает задача перехода к новому базису, формулируемая следующим образом. Пусть в пространстве R имеются два базиса: старый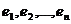 
и новый 
. Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:
.
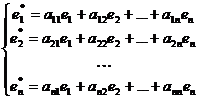Полученная система означает, что переход от старого базиса к новому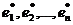 
задается матрицей перехода
,
причем коэффициенты разложения новых базисных векторов по старому базису образуют столбцы этой матрицы.
Матрица 
– невырожденная, т.к. в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базиса 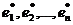к старому базису осуществляется с помощью обратной матрицы 
. Можно показать, что переход от старых координат вектора к новым и обратно осуществляется следующим образом:
и 
.
Евклидово пространство
Скалярным произведением двух векторов и 
называется число
Скалярное произведение имеет следующие свойства:
1) 
– коммутативность;
2) 
– дистрибутивность;
3) 
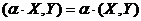для любого действительного числа 
;
4) 
, если – ненулевой вектор; 
, если — нулевой вектор.
Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам, называется евклидовым пространством.
Скалярным квадратом вектора называется следующее выражение: 
Длиной (нормой) вектора в евклидовом пространстве называется корень квадратный из его скалярного квадрата: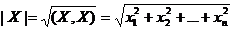 
.
Имеют место следующие свойства длины вектора:
1) 
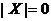тогда и только тогда, когда 
;
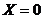2) 
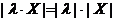, где – действительное число;
3) 
– неравенство Коши-Буняковсвкого;
4) 
– неравенство треугольника.
Угол 
между двумя векторами и 
определяется как 
, где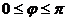 
.
Два вектора называются ортогональными, если их скалярное произведение равно нулю. Из определения следует, что если два ненулевых вектора ортогональны, то угол между ними равен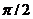 
, т.к. 
.
Векторы n -мерного евклидова пространства образуют ортогональный базис, если эти вектора попарно ортогональны, и ортонормированный базис, если эти вектора попарно ортогональны и норма каждого из них равна единице, т.е. если 
при 
и 
при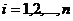 
.
Теорема. Во всяком n -мерном евклидовом пространстве существует ортонормированный базис.
