Величина, полностью характеризуемая своим числовым значением в выбранной системе единиц, называется скалярной.
Величина, кроме числового значения характеризуемая направлением, называется векторной.
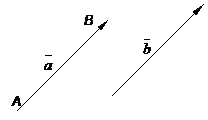В трехмерном пространстве вектор представляет собой направленный отрезок 
с начальной точкой А и конечной точкой В, который можно перемещать параллельно самому себе.
Под длиной вектора понимается его числовое значение 
без учета направления. В трехмерном пространстве это число, равное длине отрезка АВ, изображающего вектор.
Два вектора 
и 
называют равными, если они расположены на параллельных прямых, имеют одинаковые длину и направление. Если равные векторы считать одним и тем же вектором, то такой вектор называют свободным.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.
Три вектора называют компланарными, если параллельны некоторой плоскости или лежат в ней.
Осью называется направленная прямая. Для определения оси необходимо задать вектор, определяющий направление оси (его называют направляющим вектором), и точку его приложения. Заданное направление оси считается положительным, а противоположное – отрицательным.
Проекцией точки A на ось l называется основание A ' перпендикуляра AA ', опущенного из точки A на эту ось.
Компонентой вектора относительно оси l называется вектор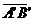 
, начало которого – точка A ' – есть проекция точки A на ось l, а конец B ' – проекция точки B на ось l.
Проекцией вектора на ось l называется скаляр 
, равный длине компоненты 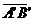относительно оси l, взятой со знаком “+”, если направление компоненты совпадает с направлением оси, и со знаком “–“ в противном случае.
Если начало и конец вектора совпадают, то такой вектор называют нулевым и обозначают 
. Длина нулевого вектора равна нулю: 
. Так как направление нулевого вектора произвольно, то считают, что он коллинеарен любому вектору.
Для задания декартовой системы координат необходимо определить произвольную точку пространства O – начало координат, 3 неколлинеарных вектора – направляющие векторы осей, и единицу измерения длины. В общем случае векторы могут не быть перпендикулярными. Их называют базисными векторами или базисом.
Говорят, что оси O x, Oy и Oz в трехмерном пространстве образуют правую тройку, если для наблюдателя, смотрящего в направлении оси Oz, кратчайший поворот оси O x к оси Oy происходит против часовой стрелки. В случае произвольных векторов понятяе правой и левой тройки вводятся следующим образом. Рассмотрим упорядоченную тройку некомпланарных векторов , , 
в трехмерном пространстве. Выберем в этом пространстве произвольную точку A и выполним параллельный перенос всех трех векторов таким образом, чтобы их начала совпали с A. Поскольку векторы некомпланарны, их концы не лежат на одной прямой и задают плоскость 
, причем через них проходит единственная окружность, лежащая в этой плоскости. Упорядоченная тройка векторов , , называется правой, если для наблюдателя, смотрящего из точки A, обход концов векторов , , по окружности осуществляется по часовой стрелке. В противном случае вектора образуют левую тройку.
Пусто O x, Oy и Oz – 3 взаимно перпендикулярные оси в трехмерном пространстве (координатные оси), исходящие из точки О (начало координат) и образующие правую тройку.
Для любой точки пространства M существует ее радиус-вектор 
с началом в начале координат и концом в данной точке. Тогда под прямоугольными декартовыми координатами точки M понимаются проекции ее радиус-вектора на соответствующие оси, т.е.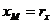 
, 
, 
.
Пусть в пространстве с декартовой системой координат Oxyz задан вектор 
. Его проекции на координатные оси 
, 
, 
называются координатами вектора в данной системе координат. При этом отношение длин проекций к длине вектора определяют косинусы углов, которые вектор образует с координатными осями. Их называют направляющим косинусами вектора и определяют из соотношений 
, 
, 
. Поскольку направляющие косинусы однозначно определяют направление вектора, он однозначно задается своими координатами.
Если известны координаты начала и конца вектора 
, 
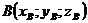, то координаты вектора определяются как 
, а его длина – как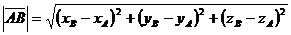 
.
Введем в рассмотрение единичные векторы (орты)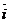 
, 
, 
, направленные по осям координат. Они образуют базис в трехмерном пространстве, взаимно перпендикулярны и имеют длину, равную единице. Такой базис называют ортонормированным. Тогда если вектор имеет координаты 
, то выражение вида 
называют координатной формой вектора или разложением вектора по базису 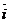, , . Это разложение единственно для каждого вектора.
В трехмерном пространстве определены следующие операции над векторами.
1. Сложение векторов
Суммой двух векторов и называют вектор , начало которого совпадает с началом вектора , а конец – с концом вектора при условии, что конец вектора совпадает с началом вектора . Если 
, 
, то 
.
2. Умножение вектора на число
Произведением вектора на число 
называется вектор 
, имеющий длину 
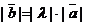, направление которого совпадает с направлением вектора , если 
, и противоположно ему, если 
. Если , то 
. Противоположным вектором 
называется произведение вектора на число (-1), т.е. 
.
Перечисленные операции обладают следующими свойствами:
1) Коммутативность сложения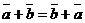 
;
2) Ассоциативность сложения 
;
3) Ассоциативность умножения на число 
;
4) Дистрибутивность умножения суммы векторов на число 
;
5) Дистрибутивность умножения вектора на сумму чисел 
;
6) Умножение вектора на ноль 
;
7) Сложение вектора с противоположным ему вектором 
;
8) Умножение вектора на единицу 
.
3. Скалярное произведение векторов
Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними, т.е.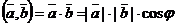 
. Если , , то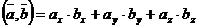 
.
Скалярное произведение векторов обладает следующими свойствами:
1)  ;
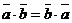2)  ;
3)  ;
| 4)  ;
5)  ;
6)  .
|
4. Векторное произведение векторов
Векторным произведением векторов и называется вектор 
, удовлетворяющий следующим условиям: 1) его длина равна произведению длин перемножаемых векторов на синус угла между ними, т.е. 
; 2) этот вектор перпендикулярен перемножаемым векторам; 3) если векторы , , неколлинеарны, они образуют правую тройку. Длина векторного произведения векторов равна площади параллелограмма, построенного на перемножаемых векторах.
Если , , то 
.
Векторное произведение векторов обладает следующими свойствами:
1. 
;
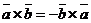2. 
;
3. 
;
4. 
.
5. Смешанное произведение векторов
Смешанным произведением векторов , и называется число 
. Смешанное произведение трех векторов равно объему параллелепипеда, построенному на этих векторах, взятому со знаком “+”, если векторы образуют правую тройку, и со знаком “–”, если они образуют левую тройку. В координатной форме смешанное произведение векторов , и 
определяется как 
.
Смешанное произведение векторов обладает следующими свойствами:
1. 
– смешанное произведение не меняется при циклической перестановке сомножителей;
2. 
– смешанное произведение при попарной перестановке сомножителей меняет знак на противоположный;
3. 
тогда и только тогда, когда векторы , и компланарны.
