СЕМИНАР ПО ГЕМОДИНАМИКЕ
Общая характеристика системы кровообращения.
Кровь в кровеносной системе непрерывно циркулирует, совершая полный оборот за 27 систол, т.е. за 20-23 секунды. Роль насоса выполняет сердце.
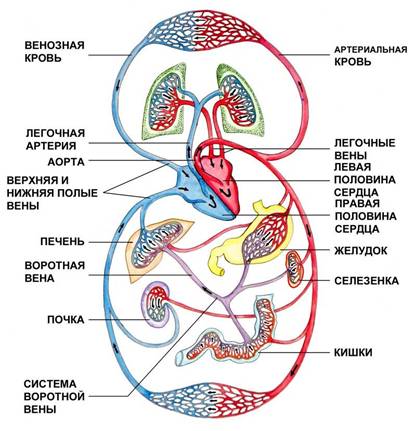
Фактически сердце выполняет функции двух насосов в последовательной гидравлической сети, которая замкнута сама на себя. Схема системы крово-обращения представлена на рис.1.
Рассмотрим последовательность прохождения полного круга некоторой порцией крови. Две части этого круга называются большим и малым кругом кровообращения.
Большой круг кровообращения начинается от левого желудочка и заканчивается правым предсер-дием. При сокращении левого
Рис. 1. Схема кровеносной системы. желудочка насыщенная кисло- родом артериальная кровь поступает в аорту, а из нее – в артерии, артериолы и капилляры всего тела. Через тонкие стенки капилляров кровь отдает клеткам тела питательные вещества и кислород, и забирает углекислый газ, превращаясь в венозную. Венозная кровь поступает по венам в правое предсердие.
Малый круг кровообращения начинается от правого желудочка и заканчивается левым предсердием. От правого желудочка по легочным артериям венозная кровь поступает в легкие, где происходит газообмен: эритроциты избавляются от углекислого газа и насыщаются кислородом. Из легких кровь по легочным венам поступает в левое предсердие, а из него – в левый желудочек. Полный круг завершен.
Поскольку эта система последовательная, количество крови, выталкиваемое при каждом сокращении левым и правым желудочками, одинаковое, и составляет, в условиях покоя, 60 – 80 мл. Этот показатель – основной показатель сократительной деятельности сердца - систолический (ударный) объем крови. При больших физических и эмоциональных нагрузках он может увеличиваться в 2-3 раза.
При стандартной процедуре измерения артериального давления (метод Короткова) фиксируются наибольшее (систолическое) и наименьшее (диастолическое) давление крови в большом круге кровообращения.
Кровеносная система не герметична: в легких она сообщается с атмосферой, иначе было бы невозможно получать из нее кислород и отдавать ей углекислый газ. Таким образом, атмосферное давление передается внутрь всех кровеносных сосудов, и вообще всех органов и систем нашего тела. Повсеместно в нашем организме действие атмосферного давления в направлении снаружи-внутрь уравновешивается его же действием в направлении изнутри-наружу. Суммарный эффект: мы не чувствуем атмосферного давления, как будто его и нет. Атмосферное давление не способствует и не препятствует циркуляции крови в кровеносной системе. Кровь циркулирует благодаря дополнительному давлению, создаваемому в кровеносной системе работающим сердцем. И при измерениях артериального давления фиксируется не абсолютное (истинное) давление в сосудах, а лишь превышение артериального давления над атмосферным.
Результат измерений 120/80 мм рт. столба означает, что максимальное давление крови, создаваемое сердцем в большом круге кровообращения - 120 мм рт. столба, минимальное – 80 мм рт. столба; среднее давление - порядка 90 мм рт. столба.
Сопоставим значения работы, которую совершают левый и правый желудочки при проталкивании одинаковых объемов крови DV. Работа, совершаемая мышцами желудочка:
∆А=р·∆V (1) Здесь р – среднее давление, создаваемое мышцами желудочка при выталкивании объема крови DV. В большом круге левый желудочек сердца создает давление, в среднем, порядка р1=90 мм рт. столба. Давление, создаваемое правым желудочком в малом круге, в среднем, порядка р2 = 15 мм рт. столба. Поскольку р1 > р2 примерно в шесть раз, а объемы DV одинаковы, то ∆А1 > ∆А2 тоже примерно в шесть раз.
Энергозатраты, подсчитанные по формуле (1), поражают своим низким уровнем. Так, в состоянии покоя работа, совершаемая за одно сокращение: левым желудочком – около 1 Дж, правым – около 0,2 Дж. Частота сердечных сокращений: 60 - 90 1/мин, то есть в среднем 75 1/мин. Средняя длительность одного цикла сокращений сердца: 60/75=0,8 секунды. Тогда средняя мощность сердца получается: (1+0,2)/0,8=1,5 Вт. При больших нагрузках мощность может достигать 8 Вт.
Общий объем крови, циркулирующей в кровеносной системе человека, порядка 5 литров. Значительная часть этого количества, около 80%, сосредоточена в венозных сосудах, обладающих свойством легко растягиваться или сжиматься, не меняя давления находящейся в них крови. Вены выполняют важнейшую функцию: они содержат большие запасы крови на случай вынужденной работы кровеносной системы в экстремальных условиях: при больших физических нагрузках или при кровопотерях организма.
Уравнение неразрывности.
Уравнение неразрывности жидкости – одно из общих уравнений гидродинамики. Рассмотрим его применительно к гемодинамике, изучающей специфику движения крови в кровеносной системе человека.
Уравнение неразрывности справедливо для несжимаемой жидкости, при условии, что поток жидкости не разветвляется и стационарен.
Поток стационарен, если его характеристики, отличаясь в разных точках или сечениях потока, остаются постоянными во времени.
Кровь – практически несжимаемая жидкость; при том избыточном давлении, которое создает сердце, плотность крови остается неизменной.
Стационарным является движение крови в капиллярах. В остальной части кровеносной системы кровоток не стационарен: периодические сердечные сокращения вызывают пульсации давления, периодические расширения кровеносных сосудов, распространение пульсовых волн.
В итоге, уравнение неразрывности применимо к движению крови на неветвящихся участках кровеносных сосудов, с использованием усредненных по времени характеристик движения крови.
Коротко о названии: что понимается под неразрывностью жидкости? Обратимся к рис. 2:
 |
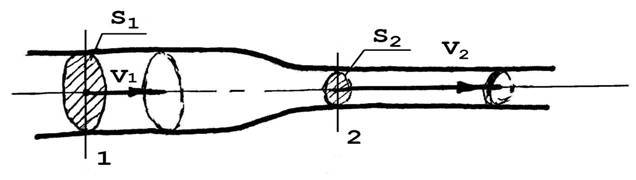Рис. 2. Движение жидкости в сужающемся потоке
Не трудно догадаться, что при движении жидкости в сужающемся потоке ее скорость возрастает: V2>V1. Неразрывность жидкости означает, что разогнавшиеся порции жидкости узкой части трубки не оторвутся от медленной жидкости ее широкой части, и между отдельными порциями жидкости не возникнет разрывов и пустот.
Теперь – о самом уравнении неразрывности. Его идея очень проста: на любом неразветвленном участке сети какой объем жидкости за единицу времени втекает, такой и вытекает: ведь кровь практически несжимаема. Для условий рис. 2: сколько жидкости перетекает за секунду через сечение S1, столько же пройдет через сечение S2, и через любое сечение от входа до выхода.
На рис. 2 слева выделен цилиндр, опирающийся на сечение площадью S1. За интервал времени Dt = 1с частицы жидкости, вошедшие в этот объем первыми, сместятся вправо на расстояние, равное скорости V1, и первыми из него выйдут. То есть за это время на этом участке произойдет полная замена жидкости.Следовательно, объем цилиндрика S1V1 – это объем жидкости, прошедшей через сечение S1 за D t = 1с. Точно такой же объем, но представленный сомножителями S2 и V2, пройдет за одну секунду и через сечение 2. Требование одинаковости этих объемов приводит к уравнению неразрывности:
S1 V1 = S2 V2 , или SV = Const (2)
Величина Q = SV – объемный расход жидкости - имеет смысл объема жидкости, протекающей через поперечное сечение потока в единицу времени. Для системы кровообращения в целом, эта величина называется общим объемом кровотока. Для взрослого человека в спокойном его состоянии, в среднем,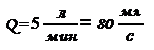 
.
С помощью уравнения неразрывности можно согласовать значения скорости кровотока в аорте и в капиллярах. В спокойном состоянии человека скорость кровотока в аорте – порядка V1 = 0,4 м/с. Измерения под микроскопом показывают, что скорость в капиллярах – V2 = 0,5 мм/с = 5×10-4 м/с. Эти значения отличаются друг от друга в 800 раз. Следовательно, если площадь сечения аорты S1 = 4 см2, то общая площадь поперечных сечений системы капилляров большого или малого круга кровообращения больше, чем S1, в 800 раз, и составляет S2 = 3200 см2 = 3,2×103 см2.
Получив эти данные, оценим степень ветвления общего потока крови в системе капилляров. Диаметр капилляра d = 10 мкм = 0,01 мм = 10-3 см; следовательно, площадь его сечения s = pd2/4 = 0,78×10-6 см2. Стало быть, кровь из аорты разветвляется в системе капилляров на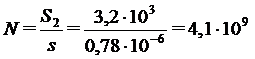 
штук. Можно прикинуть суммарную протяженность этих параллельно работающих капилляров. Принимая среднее значение их длины l = 0,7 мм, получаем суммарную протяженность капилляров:
L = Nl = 4,1×109×0,7 = 2,9×109 мм = 2,9×106 м = 2900 км.
Этот результат следует удвоить: в системе кровообращения – две последовательные системы капилляров. Получаем, что общая протяженность всех капилляров нашего организма – порядка 5800 км.
Мы рассмотрели упрощенную модель системы кровообращения, и получили впечатляющий, но – заниженный результат. Истинная суммарная протяженность капилляров нашего организма – порядка 100000 км, что достаточно, чтобы опоясать Землю 2,5 раза!
Уравнение Бернулли.
Уравнение Бернулли еще одно важное уравнение общей гидродинамики. Оно справедливо для стационарных потоков жидкости, в которой отсутствуют силы вязкого трения.
Сразу заметим; вязкость крови - важный диагностический показатель состояния кровеносной системы. Кроме того, как уже отмечалось, система кровообращения существенно нестационарна. Следовательно, уравнение Бернулли можно применять в гемодинамике с разумной осторожностью: для небольших участков кровеносной системы, и при этом подставлять в это уравнение усредненные по времени величины.
Уравнение Бернулли соответствует закону сохранения механической энергии при движении жидкости и верно в той степени, в которой потери на трение пренебрежимо малы. Оно имеет следующий вид:
р0 = р + rgh + rV2/2 = Const (3)
Здесь p0 – полное давление на рассматриваемом участке. Оно представлено в уравнении как сумма трех слагаемых. Остановимся на каждом из них и на их связи с понятием «энергия» подробнее.
3.1. Слагаемое р – статическое давление. Оно действует на стенки сосудов и на все, что в жидкости находится: если речь о кровеносных сосудах, то статическое давление действует не только на их стенки, но и на форменные элементы, и на бляшки, прилипшие к стенкам, и на микропузырьки газов, имеющиеся в крови. Важная особенность статического давления: оно всегда действует перпендикулярно поверхности, какой бы сложной эта поверхность ни была. Если бы это было не так, то у силы давления появилась бы составляющая, направленная по касательной к поверхности, и она вызывала бы течение вдоль поверхности, а этого не бывает.
Еще одна особенность статического давления – характер его связи с категорией «энергия». Проследим цепочку преобразований единицы измерения статического давления:
1 Па = 1 Н / м2 = 1 Н·м / м3 = 1 Дж / м3.
Получили, что один паскаль численно равен энергии единицы объема жидкости (или газа). Какого вида энергии? Силы статического давления способны совершать механическую работу, если тело, на которое они действуют, имеет возможность перемещаться. Потенциальная возможность совершения работы означает, что жидкость или газ, оказывающие статическое давление, обладают потенциальной энергией.
Своеобразие ситуации с этой потенциальной энергией состоит в том, что джоули – есть, а единого механизма их появления – нет; их наличие всегда объяснимо, но объяснения могут быть в разных случаях разными, нет строгой классической однозначности.
За счет сил статического давления кровь движется вдоль кровеносных сосудов, из области повышенного давления в область пониженного. Потенциальная энергия статического давления переходит в кинетическую энергию движения крови.
3.2. Слагаемое ρ gh – гидростатическое давление. Выражение ρgh ассоциируется с выражением mgh потенциальной энергии тела массы m, находящегося на высоте h. И правильно делает, что ассоциируется. Гидростатическое давление ρgh – это и есть потенциальная энергия единицы объема жидкости, находящейся на высоте h; эта энергия обусловлена гравитационным притяжением к Земле жидкости, имеющей плотность ρ. Высоту h отсчитывают от уровня, условно принятого за нулевой.
Силы гравитации, создающие гидростатическое давление, и силы инерции, проявляющиеся в условиях перегрузок, знакомых военным летчикам, космонавтам, автогонщикам, - эти две силы бывают очень похожи по характеру вызываемых ощущений и могут оказаться вообще неотличимыми друг от друга. Перегрузка как измеряемая величина – это отношение ускорения a, которое испытывает, к примеру, летчик к величине ускорения свободного падения g. На время действия перегрузок в кровеносной системе и во всем организме действует дополнительное гидростатическое давление r a h. Оно действует не вместо давления ρ g h, а наряду с ним. Но векторы a и g не всегда совпадают по направлению.
При больших перегрузках система кровообращения может оказаться далеко за пределами условий, на которые она природой рассчитана. Считается, что организм без особых расстройств справляется с 8-кратной перегрузкой в течение трех секунд, а с 5-кратной – при ее продолжительности 12–15 секунд.
Для длительной работа кровеносной системы в условиях перегрузок требуются крепкое здоровье и тренировки на специальных тренажерах, например – на центрифуге.
Перегрузки неотличимы от возросшей гравитации как для человека, так и для любых измерительных приборов. Это утверждение соответствует принципу эквивалентности гравитации и инерции, сформулированному Эйнштейном.
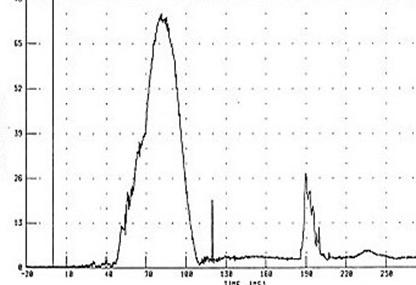
Чтобы испытать большие перегрузки, не обязательно становиться военным летчиком или космонавтом. Большие перегрузки испытывают участники дорожно-транспортных происшествий, их транспортные средства и пешеходы – участники ДТП. На рис. 3 приведена запись ускорения при краш-тесте легкового автомобиля.
|
б
Рис. 3. Результаты краш-теста.
Уменьшение последствий столь больших перегрузок для водителей и пассажиров достигается увеличением длительности гашения их скорости с помощью ремней и подушек безопасности. Кое-что зависит при этом и от конструкции автомобилей: они не должны быть чрезмерно прочными, временной график их разрушения при аварии должен отвечать той же идее увеличения длительности.
3.3. Слагаемое ρ V 2 / 2 – динамическое давление. У большинства это выражение ассоциируется с выражением для кинетической энергии: mV2 / 2. Ассоциация вполне уместная: динамическое давление – это кинетическая энергия единицы объема жидкости, имеющей скорость V.
Главная особенность динамического давления состоит в том, что оно
не является давлением в привычном смысле: оно не действует на стенки сосуда и на предметы, которые поток обтекает. Но оно проявит себя во всех своих паскалях при торможении потока: то, что до торможения было динамическим давлением, станет при торможении статическим давлением, действующим на остановившую поток преграду. В остановленном потоке динамическое давление равно нулю.
Вот пример проявления динамического давления. При измерениях артериального давления наблюдаются колебания стрелки манометра в такт с турбулентными шумами, которые прослушиваются на локтевом сгибе при «засечке» систолического давления. Они возникают в связи с появлениями и исчезновениями просвета в артерии, сжатой манжетой, при прохождении пульсовой волны. Кровь в просвете артерии, возникающем в моменты систолы, имеет большую скорость (порядка 4 м/с). Кратковременное появление динамического давления приводит, в соответствии с уравнением Бернулли, к кратковременному уменьшению статического давления крови на стенку артерии. Это повторяется при каждом сердечном сокращении. Стрелка манометра отслеживает пульсации статического давления. При этом максимальное давление крови в систоле – это тот максимум, который успевает показать колеблющаяся стрелка манометра и который следует записать как систолическое давление в протокол измерений.
В уравнении Бернулли (3) p 0 – полное давление на участке гидравлической сети. Мы убедились, что все три слагаемых полного давления имеют смысл различных видов механической энергии единичного объема текущей жидкости. Тогда полное давление – это полная механическая энергия единицы объема текущей жидкости, и энергетический смысл уравнения Бернулли предельно прост: полная механическая энергия стационарного потока жидкости есть величина постоянная, если потери энергии на преодоление сил трения пренебрежимо малы. П одчиняясь условиям течения, слагаемые величины p 0 могут меняться, но непременно так, чти их сумма будет оставаться постоянной.
В качестве примера полезности уравнения Бернулли, рассмотрим особенности статического давления в гидравлической линии постоянного поперечного сечения, представленной на рис. 3. Ее участки находятся на различной высоте.
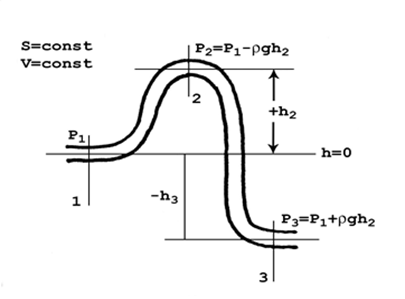
Рис.4. К уравнению Бернулли.
Положим, что какой-то насос поддерживает в сечении 1 постоянное статическое давление p1. Так как площадь сечения сети постоянна, то скорость V и динамическое давление rV2/2 тоже постоянны.
Тогда уравнение Бернулли для участка между сечениями 1 и 2 запишется:
p1 + rV2 / 2 + 0 = p2 + rV2 / 2 + rgh2
Здесь в левой части – полное давление в сечении 1, а в правой – в сечении 2. После сокращения одинаковых значений динамических давлений, получаем:
p1 = p2 + rgh2
Отсюда следует:
p2 = p1 - rgh2, то есть p2 ˂ p1.
Аналогично, для участка между сечениями 1 и 3 после сокращений уравнение Бернулли принимает следующий вид:
p1 = p3 - rgh3,
Отсюда следует:
p3 = p1 + rgh3, то есть p3 > p1. 
Мы убедились, что статическое давление в приподнятых участках меньше, чем давление p1 на входе, а на опущенных – оно, наоборот, превосходит входное.
Применительно к кровеносной системе: все, что находится выше уровня сердца, испытывает пониженное статическое давление (а это, в частности, мозг), а все, что ниже (ноги, например) -находится под давлением, превосходящим созданное сердцем. Для мозга действие гидростатического давления меняет статическое примерно на -30 мм рт. ст., а для ног эта «поправка» составляет около +110 мм рт. ст. Но система кровообращения имеет механизмы регулирования, вносящие поправки на снабжение кровью органов, находящихся в неравных условиях.
Движение крови в реальной кровеносной системе сопровождается не постоянством (как у Бернулли), а постепенным уменьшением полного давления крови: энергия сердечного сокращения расходуется на преодоление сил вязкого трения и других сил сопротивления. На подходе к правому предсердию этот избыток давления, созданный левым желудочком, становится близким к нулю. Полное давление как сумма статического и динамического давлений, становится все меньше и наконец становится равным нулю:
р0 = р + rV2/2 = 0
Отсюда следует, что при достаточно большой скорости крови статическое давление может оказаться отрицательным:
р = -rV2/2
Этот результат означает, что давление в таких венах может быть несколько ниже атмосферного, и при их повреждении возможна воздушная эмболия – попадание воздуха в полости сердца. На реальном сердце такое статическое давление, которое можно называть разрежением, может составлять величину порядка - 3 мм рт. столба. Тонкостенные эластичные вены при этом временно спадают.
Режимы течения жидкостей.
Различают два вида течения жидкостей: ламинарное и турбулентное.
Ламинарное течение характерно для медленных потоков: это спокойное, упорядоченное движение. Перемешивание слоев чрезвычайно слабое: оно происходит лишь за счет молекул, совершающих тепловое хаотическое движение.
В ламинарных потоках распределение скорости жидкости в поперечном сечении очень неравномерное: на рис. 5А мы видим сочетание медлительных пристеночных слоев с очень быстрым движением жидкости в ядре потока. Получается, что при ламинарном течении площадь поперечного сечения потока используется неэффективно: основная часть объемного расхода жидкости Q переносится в ядре потока, площадь которого невелика.
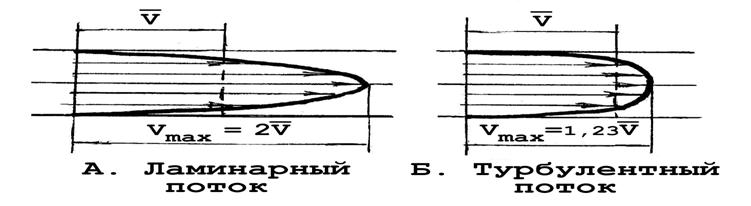
Рис. 5. Особенности ламинарного и турбулентного потоков.
Турбулентное течение (от лат. turbulentus - беспорядочный) характерно для быстрых потоков. Взаимодействие соседних слоев турбулентного потока очень интенсивное: на границах слоев возникают временные образования – вихри различного масштаба. Вихри способствуют интенсивному перемешиванию жидкости и выравниванию скоростей в поперечном сечении потока: распределение скоростей становится ближе к равномерному (рис. 5 Б), что способствует росту пропускной способности трубопровода или кровеносного сосуда. Но за все приходится платить: появление турбулентных вихрей в потоке крови – это появление дополнительного вида движения в ней, на которые необходимы дополнительные затраты энергии работающего сердца.
Турбулентные потоки сопровождаются шумами. Совокупность возникающих-исчезающих вихрей приводит к появлению пульсаций статического давления, действующего на стенки сосуда.
Звуки, созданные турбулентными вихрями крови в артерии, прослушиваются через фонендоскоп при измерении артериального давления по методу Короткова.
Переход от ламинарного режима к турбулентному происходит, если поток достигает некоторого критического значения критической скорости. Экспериментально установлено, что критическая скорость Vкр прямо пропорциональна динамической вязкости жидкости η и обратно пропорциональна плотности жидкости ρ и диаметру d сосуда:
Vкр ̴ η / ρ d
Изучение связи этих показателей при ламинарном и при турбулентном режиме течения привело к созданию безразмерного критерия – числа Рейнольдса, которое можно назвать индикатором режима течения жидкости.
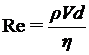(4)
Здесь r - плотность жидкости; h - динамическая вязкость; V – средняя скорость жидкости в рассматриваемом сечении потока; d – диаметр сосуда в этом сечении.
Как пользоваться этим индикатором? Надо вычислить по формуле (4) значение числа Рейнольдса Re для условий рассматриваемого потока и полученный результат сравнить с критическим значением числа Рейнольдса для данной жидкости – величиной Reкр.
При Re ˂ Reкр условия в потоке соответствуют ламинарному режиму.
При Re > Reкр в потоке установится турбулентный режим.
Для различных жидкостей значение Reкр различно. Для воды Reкр = 2300.
Для крови Reкр = 970 ± 80.
Повод для размышлений: в кровеносном сосуде диаметром 2,5 мм значение Re кр достигается при скорости движения крови около 4 м/с. Вопрос: каким станет режим течения в этом кровеносном сосуде, если увеличить любой один параметр правой части формулы (4)?
Отметим, что для перевода режима течения жидкости из турбулентного в ламинарный требуется такое снижение скорости, при котором Re «Reкр. Это означает, что ламинарный режим течения легче разрушить, чем потом восстановить.
Турбулентный режим может установиться при значениях числа Рейнольдса, гораздо меньших, чем критическое. Разрушителями ламинарного течения могут оказаться шероховатые стенки, резкие повороты потока, выступающие в поток элементы измерительных устройств. В кровеносных сосудах это могут быть склеротические бляшки на их стенках.
В заключение отметим, что атмосферные циклоны и антициклоны – это вихри гигантского масштаба - проявления неустойчивости воздушных потоков в атмосфере нашей планеты.
Формула Пуазейля.
В тонких длинных трубках с ламинарным режимом течения жидкости выполняется соотношение, полученное Пуазейлем и Стоксом и известное как формула Пуазейля:
(5)
Здесь Q – объемный секундный расход жидкости, (м3/с);
Dр – перепад давлений на трубке: ∆р = рвх – рвых, (Па);
l – длина трубки, (м);
r – ее радиус, (м);
h - динамическая вязкость жидкости, (Па·с).
Формула фиксирует важную причинно-следственную связь объемного секундного расхода жидкости Q и перепада давления Dр на трубке. Даже если давление на концах трубки очень большое, но одинаковое, то ∆р = 0, и
течение жидкости в трубке не возникнет, но чем больше Dр, тем больше Q. Чтобы выделить значимость этой связи, формулу Пуазейля часто применяют в виде:
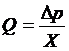, где 
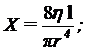(6)
Здесь Х – гидравлическое сопротивление трубки, учитывающее внутренний радиус трубки, ее длину и динамическую вязкость протекающей по ней жидкости.
Особо заметен в формуле гидравлического сопротивления множитель r4: влияние радиуса сосуда на его гидравлическое сопротивление чрезвычайно сильное. К примеру, если радиус r изменить в два раза, то величина r4 изменится в 16 раз! В 16 раз изменится и гидравлическое сопротивление сосуда. Это влияние проявляется, в частности, при развитии гипертонического криза – тяжелого состояния, вызванного чрезмерным повышением артериального давления.
При развитии криза имеет место следующая цепочка событий в кровеносной системе: сбой в системе сосудистой регуляции → спазм артериол (то есть уменьшение их радиуса) → повышение их гидрав-лического сопротивления → повышение частоты сердечных сокращений → резкий рост артериального давления → дополнительная нагрузка на систему сосудистой регуляции → дополнительный спазм, и т д. – круг замкнулся, система пошла вразнос.
Как первоочередная мера при подобных состояниях – применение спазмолитиков – препаратов, снимающих спазмы и обладающих сосудорасширяющим действием (коньяк и др.).
Формула Пуазейля имеет полезное алгебраическое следствие:
Х =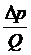 
(7)
Это выражение можно использовать для экспериментального определения величины гидравлического сопротивления Х реального кровеносного сосуда. В гемодинамике формула (6) нашла применение для ͞оценки гидравлического сопротивления большого круга кровообращения. В кардиохирургии этот важный показатель состояния сердечно-сосудистой системы принято называть так: общее периферическое сопротивление сосудов (ОПСС) и оценивать по формуле:
ОПСС = 
(8)
Здесь Q – общий объем кровотока;
͞p - среднее артериальное давление: ͞p = рд + 1/3 (рс - рд)
ЦВД – центральное венозное давление – то есть давление в правом предсердии; в норме это 6 -12 мм рт. столба.
Пример вычислений. При артериальном давлении 120 / 80 мм рт. столба давление: ͞p–ЦВД = 93,3–9 мм рт. ст.=84,3мм рт. ст.·(133Па/мм рт. ст.)= =11,2·103Па. Полагая Q = 80 мл /с = 0,08 л/с, получаем ОПСС = 140 кПа·с /л.
В норме ОПСС - в пределах 80 – 150 кПа·с /л.
ОПСС не может быть непосредственно измеренным; во всяком случае в настоящее время это – так. В то же время повсеместно отмечается важность и ценность этого показателя. Из формулы (8) следует, что чем больше артериальное давление, тем больше ОПСС, и наоборот. Но экспериментальные исследования показывают, что эта простая линейная связь может нарушаться: в правой части формулы (8) есть не только числитель, но и знаменатель. Выше, в примере вычислений ОПСС, величина Q была принята на уровне среднестатистической нормы и молчаливо полагалась величиной постоянной. Но это, как выясняется, не всегда так.
В заключение этого параграфа – предложение для продвинутых студентов: рассмотреть аналогию между формулой Пуазейля и законом Ома для участка электрической цепи. Что на что похоже? Глубока или поверхностна эта аналогия? И вообще…
