Послідовність виконання роботи.
1. Згрупувати емпіричні дані. Визначити найбільше tn і найменше t1 значення елементів вибірки. Обчислити по формулі (1.1) приблизна кількість інтервалів групування. Визначити по формулі (1.2) ширину інтервалів групування.
За допомогою табл. 1.2. розрахувати частоти улучення випадкової величини в інтервал групування
2. Побудувати графік - гістограму. Значення, отримані в графах 1–3, 5 табл.1.2. перенести в графи 1, 2, 3 табл. 1.6.
Таблиця 1.6. Послідовність обчислень при перевірці приналежності даних нормального закону.
| j |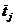 
| mj | 
| 
| 
| 
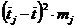
| Yj | fэ(tj) | f(tj) | Fэ(tj) | F(tj) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Обчислити по формулі (1.3) значення емпіричної функції розподілу і вписати її в графу 11 табл. 1.6.
Обчислити по формулі (1.4) значення емпіричної щільності розподілу імовірностей. Отримані значення вписати в графу 9 табл. 1.6. і побудувати по них гістограму.
3. Прийняти гіпотезу щодо виду закону розподілу.
4. Дати оцінку параметрам закону розподілу. Розрахувати по формулі (1.5) оцінку математичного чекання. Розрахувати графи 5, 6, 1 табл. 1.6 і дати оцінку середнього квадратичного відхилення:
.
Дати оцінку коефіцієнту варіації.
.
І відповідно до його значень перевірити справедливість висунутої гіпотези щодо закону розподілу.
5. Визначити теоретичні характеристики розподілу. Розрахувати центровані і нормовані відхилення середніх інтервалів
і внести значення в графу 8 табл. 1.6.
Обчислити значення теоретичної функції розподілу:
,
де значення Ф(х) знайти в табл.1.3 додатка. Отримані значення записати в графу 12 табл.1.6.
Визначення значення теоретичної щільності розподілу імовірностей.
,
де значення f0(x) знайти в табл.1.4 додатка. Отримані значення вписати в графу 10 табл. 1.6.
6. Виконати перевірку погодженості між емпіричними і теоретичними розподілами.
Перенести значення граф 2, 11, 12 табл. 1.6. у графи 1, 2, 3 табл. 1.7.
Таблиця 1.7. Послідовність обчислення відхилень функції.
| tj | Fэ(tj) | F(tj) | Fэ(tj)–F(tj) |
| 1 | 2 | 3 | 4 |
Знайти максимальне відхилення між функцією емпіричного і теоретичного розподілу
.
Обчислити величину:
.
Задатися довірчою імовірністю
того, що відхилення Fэ(tj) від F(tj) буде менше величини 
, що знаходиться в табл. 1.5 додатка і яка встановлена для довірчої імовірності.
Зробити висновок щодо відповідності емпіричних даних обраної моделі закону розподілу. Перевірити гіпотезу щодо виду розподілу коефіцієнтів асиметрії й ексцесу.
Перенести значення граф 1, 2, 3, 5 табл.1.6. у графи 1, 2, 3, 4 табл.1.8. Розрахувати графи 5 і 6 табл.1.8. і визначити коефіцієнт асиметрії.
.
Розрахувати графи 7 і 8 табл.1.8. і дати оцінку коефіцієнта ексцесу:
.
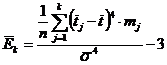Таблиця 1.8. Послідовність обчислення коефіцієнтів асиметрії й ексцесу.
| j |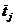
| mj |
| 
| 
| 
| 
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Зробити висновок щодо погодженості емпіричних даних нормальному закону розподілу.
7. Визначити довірчі границі параметрів закону розподілу,
Обчислити нижню і верхню однобічної довірчої границі математичного чекання.
;
,
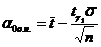де τγ1,2 вибирається з табл.1.6 додатка в залежності від прийнятої довірчої імовірності γ.
Розрахувати нижню і верхню однобічної довірчої границі середньоквадратичного відхилення.
;
де коефіцієнти Zн, Zв – визначити в залежності від прийнятої довірчої імовірності γ і числа ступенів волі k=n–1, по рівняннях:
;
,
тут коефіцієнт Uγ вибрати по табл.1.2 додатка.
8. Дати оцінку показників надійності.
Оцінка середнього ресурсу знаходиться по формулі (1.5). По формулах (1.35) і (1.36) розраховуються нижня і верхня довірчі границі середнього ресурсу.
Дати оцінку імовірності безвідмовної роботи для заданого наробітку.
,
де значення Ф(х) – вибрати по таблиці 1.2 додатка.
Дати оцінку інтенсивності відмовлень для заданого наробітку
.
Дати оцінку гамма-процентного ресурсу при заданому значенні
.
9. Побудувати характеристики надійності.
