Для русла прямоугольного сечения шириной b и глубиной потока h площадь поперечного сечения 
. Погружение центра тяжести 
.
Удельный расход потока 
.
Основное уравнение гидравлического прыжка (8.51) для прямоугольного сечения принимает вид
. (8.54)
Ширина сечения 
; 
.
Выполнив преобразования, получим
. (8.55)
Учитывая, что 
, получим
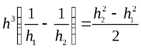(8.56)
или
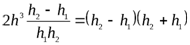. (8.57)
Окончательно получим квадратное уравнение относительно 
, и 
:
. (8.58)
Решая уравнение в отношении , и , находим уравнения для вычисления сопряженных глубин прыжка в прямоугольном русле:
. (8.59)
. (8.60)
В пределах длины гидравлического прыжка происходят относительно большие потери механической энергии, которые обусловлены интенсивностью пульсаций скоростей в прыжке.
Для прямоугольного горизонтального русла гидравлические потери можно определить из уравнения Бернулли для потоков в открытых руслах:
;
; (8.61)
Отсюда гидравлические потери
. (8.62)
Критическая глубина
.
После подстановки 
в выражение (8.62) получим
. (8.63)
Из уравнения сопряженных глубин в прямоугольном русле (8.58) критическая глубина
(8.64)
Решая совместно (8.63) и (8.64), уравнение гидравлических потерь в прыжке для прямоугольного русла имеет следующий вид:
, (8.65)
где 
- высота гидравлического прыжка.
Длина гидравлического прыжка определяется по формулам, которые были получены в результате экспериментальных исследований. Наиболее употребляемыми формулами для расчета длины прыжка являются:
формула Павловского:
; (8.66)
формула Чертоусова:
, (8.67)
где Fr - число Фруда для начального участка прыжка с глубиной :
;
• формула Сафранеца:
. (8.68)
В гидравлическом прыжке происходит резко неравномерное распределение скорости в его сечениях. На начальном участке большие скорости около дна русла и по мере продвижения потока к концу гидравлического прыжка распределение скорости сильно изменяется. При удалении от прыжка эпюра распределения скоростей постепенно начинает приобретать вид, соответствующий равномерному движению потока. Расстояние от конца прыжка до сечения, где эпюра распределения скорости соответствуют эпюре равномерного потока, называется длиной послепрыжкового участка 
. Эту длину рекомендуется принимать равной 
длинам гидравлического прыжка: 
.
♦ Пример 8.3
В канале трапецеидального сечения образовался гидравлический прыжок. Глубина в начале прыжка 
м. Требуется определить сопряженную с ней глубину прыжка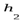 
при следующих данных: 
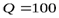м3/с; 
м; 
.
Используем условие прыжковой функции 
. Площадь сечения 
, расстояние центра тяжести сечения ус относительно свободной поверхности в канале
.
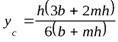Прыжковую функцию можно представить в виде
.
Подставив в это выражение численные значения Q, b, m, окончательно получим
.
Используя последнее выражение, задаваясь разными значениями h, вычисляем прыжковую функцию. Результаты вычислений сводим в табл. 8.4.
Таблица 8.4 - Вычисление прыжковой функции
 , м
| 
| 
|  , м3
|
| 0,3 | 132,82 | 1,09 | 140,9 |
| 0,5 | 83,21 | 3,04 | 86,2 |
| 0,8 | 51,37 | 7,85 | 59,2 |
| 1,0 | 40,77 | 12,33 | 53,1 |
| 1,3 | 26,64 | 28,13 | 54,8 |
| 2,0 | 19,60 | 50,64 | 70,2 |
| 2,5 | 53,23 | 80,19 | 95,4 |
| 3,0 | 12,58 | 117,00 | 129,6 |
| 3,5 | 11,67 | 161,33 | 173,2 |
По данным табл. 8.4 построим график функции 
(рис. 8.15).
Рис. 8.15. График прыжковой функции к примеру 8.3
Зная первую глубину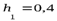 
м, по графику находим сопряженную с ней глубину 
м. Этим глубинам соответствует функция 
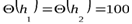м3.
