Положение любой частицы жидкости относительно некоторой произвольной линии нулевого уровня 0-0 определяется вертикальной координатой Z. Для реальных гидравлических систем это может быть уровень, ниже которого жидкость из данной гидросистемы вытечь не может. Например, уровень пола цеха для станка или уровень подвала дома для домашнего водопровода.
- Как и в гидростатике, величину Z называют нивелирной высотой.
- Второе слагаемое -
носит название пьезометрическая высота. Эта величина соответствует высоте, на которую поднимется жидкость в пьезометре, если его установить в рассматриваемом сечении, под действием давления P. - Сумма первых двух членов уравнения
¾ гидростатический напор. - Третье слагаемое в уравнения Бернулли
называется скоростной высотой или скоростным напором. Данную величину можно представить как высоту, на которую поднимется жидкость, начавшая двигаться вертикально со скорость u при отсутствии сопротивления движению. - Сумму всех трёх членов (высот) называют гидродинамическим или полным напором и, как уже было сказано, обозначают буквой Н.
В 
се слагаемые уравнения Бернулли имеют размерность длины и их можно изобразитьграфически.
Значения 
- нивелирную, пьезометрическую и скоростную высоты можно определить для каждого сечения элементарной струйки жидкости. Геометрическое место точек, высоты которых равны 
, называется пьезометрической линией. Если к этим высотам добавить скоростные высоты, равные 
, то получится другая линия, которая называется гидродинамической или напорной линией.
Из уравнения Бернулли для струйки невязкой жидкости (и графика) следует, что гидродинамический напор по длине струйки постоянен.
Энергетическая интерпретация уравнения Бернулли
Выше было получено уравнение Бернулли с использованием э 
нергетических характеристик жидкости. Суммарной энергетической характеристикой жидкости является её гидродинамическийнапор.
С физической точки зрения это отношение величины механической энергии к величине веса жидкости, которая этой энергией обладает. Таким образом, гидродинамический напор нужно понимать как энергию единицы веса жидкости. И для идеальной жидкости эта величина постоянна по длине. Таким образом, физический смысл уравнения Бернулли это закон сохранения энергии для движущейся жидкости.
Здесь с энергетической точки зрения (в единицах энергии, Дж/кг) gz — удельная потенциальная энергия положения; Р/ r — удельная потенциальная энергия давления; gz + Р/ r — удельная потенциальная энергия; u2/2 — удельная кинетическая энергия; и — скорость элементарной струйки идеальной жидкости.
Умножив все члены уравнения на удельный вес жидкости g, получим
g z - весовое давление, Па; P — гидродинамическое давление, Па; r и2 /2 — динамическое давление Па; g H — полное давление, Па
Уравнение Бернулли для потока идеальной жидкости
П 
оток идеальной жидкости, как указывалось ранее, можно представить совокупностью элементарных струек жидкости. Скорости по сечению потока неодинаковы, причём в середине потока скорости наибольшие, а к периферии они уменьшаются (струйная модель потока). Это означает, что различные струйки в одном сечении имеют различные значения кинетической энергии. Отсюда следует, что кинетическая энергия, посчитанная с использованием скоростей элементарных струек uS, и кинетическая энергия, посчитанная с использованием значения средней скорости потока V, будет иметь разные значения. Выясним, какова эта разница. Кинетическая энергия элементарной струйки 
равна:
где 
- масса жидкости плотностью 
, протекающей через живое сечение элементарной струйки 
со скоростью 
за время dt, равная:
.
Проинтегрировав выражение для 
, получим выражение для кинетической энергии потока идеальной жидкости 
.
.
Если принять, что t=1, получим:
.
Последняя формула определяет энергию потока с использованием скоростей элементарных струек uω.
Если получить значение кинетической энергии потока с использованием значения средней скорости потока V, получим формулу:
,
где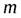 
- масса жидкости плотностью 
, протекающей через живое сечение потока 
со скоростью 
за время t, равная:
.
После подстановки при t=1 окончательно получим:
.
Отношение 
и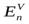 
, равное:
.
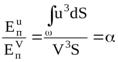Полученная величина α носит наименование коэффициента кинетической энергии или коэффициента Кориолиса. Смысл этого коэффициента заключается в отношении действительной кинетической энергии потока в определённом сечении к кинетической энергии в том же сечении потока, но при равномерном распределении скоростей. При равномерном распределении скоростей его значение равно единице, а при неравномерном – всегда больше единицы и для любого потока его значение находится в пределах от 1 до 2 и более.
Учитывая коэффициент кинетической энергии, приведём уравнение Бернулли для потока идеальной жидкости, которое примет вид:
Надо учесть, что в общем случае в разных сечениях потока коэффициент α будет иметь различные значения.
Диаграмма уравнения Бернулли представляет собой геометрическую интерпретацию, которая в графическом виде отображает изменения удельной энергии потока, то есть энергии, отнесенной к единице веса жидкости.
Диаграмма уравнения Бернулли состоит из пьезометрической линии P-P, отображающей изменение удельной потенциальной энергии и гидродинамической линии Е-Е, отображающей изменение удельной механической энергии.
Для двух любых контрольных сечений потока уравнение Бернулли записывается
Пьезометрическая линия расположена от плоскости сравнения 0-0 на расстоянии Z +P/γ;
Гидродинамическая линия расположена от плоскости0-0 на расстоянии Z+P/γ + £V2/2g
Величина Н= Z+ P/γ+ £V2/2g называется гидродинамическим напором.
Гидродинамическая линия имеет уклон вдоль потока, который называется гидродинамическим уклоном. Уклон пьезометрической линии, называется пьезометрическим уклоном.
Пьезометрическая и гидродинамическая линия на участках местных сопротивлений условно изображаются вертикальным уступом.
Высота уступа гидродинамической линии графически изображает местную потерю напора hm, то есть ту часть энергии, которая вследствие местных сил трения обращается во внутреннюю, тепловую энергию и поэтому считается потерянной.
Тема 3. Гидравлические сопротивления, причины возникновения, классификация, примеры расчета.
Графики Никурадзе.
График Никурадзе
Если для гидравлически гладких труб коэффициент потерь на трение вполне определяется числом Рейнольдса, то для шероховатых труб 
зависит ещё и от шероховатости внутренней поверхности трубы. При этом важен не абсолютный размер 
бугорков шероховатости, а отношение этого размера к радиусу (или диаметру) трубы, т.е. так называемая относительная шероховатость 
. Одна и та же абсолютная шероховатость может совершенно не оказывать влияния на сопротивление трубы большого диаметра, но способна значительно увеличить сопротивление трубы малого диаметра. Кроме того, на сопротивление влияет характер шероховатости. Простейшим случаем будет тот, когда все бугорки шероховатости имеют один и тот же размер 
и одинаковую форму, т.е. при так называемой равномерно распределённой зернистой шероховатости.
Таким образом, в этом случае коэффициент зависит как от Рейнольдса, так и от отношения (или 
):
(1.83)
Характер влияния этих двух параметров на сопротивление труб отчётливо виден из графика, который является результатом опытов И.И. Никурадзе.
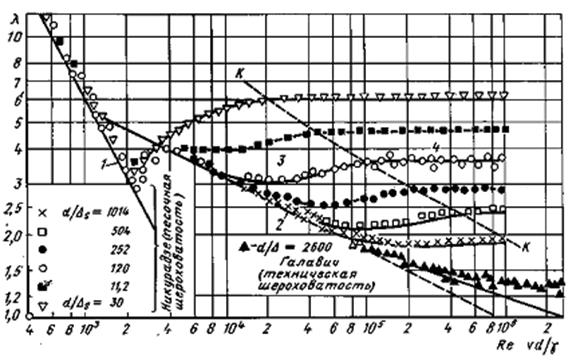
Рис 1.23. Экспериментальная зависимость гидравлического коэффициента трения А, от числа Рейнольдса 
и относительной гладкости при песочной шероховатости (график Никурадзе)
И.И. Никурадзе испытал на сопротивление ряд труб с искусственно созданной шероховатостью на их внутренней поверхности. Шероховатость была получена путём приклейки песчинок определённого размера,. Полученного просеиванием песка через специальные сита. Тем самым была получена равномерно распределённая зернистая шероховатость. Испытания были проведены при широком диапазоне относительных шероховатостей (
), а также чисел
Рис. 2.24. Экспериментальные зависимости гидравлического коэффициента трения 
от числа Рейнольдса 
и относительной гладкости стенок для промышленных труб с неравномерной шероховатостью
Re (
). Результаты этих испытаний представлены в виде кривых зависимости 
от 
для ряда значений .
Из графика можно сделать следующие выводы:
- При ламинарном течении шероховатость на сопротивление не влияет.
- Критическое число Рейнольдса от шероховатости практически не зависит;
- В области турбулентного течения, но при небольших Re и шероховатость на сопротивление не влияет;
- При больших Re и больших относительных шероховатостях коэффициент
перестаёт зависеть отRe и становится постоянным для данной относительной шероховатости.
