Основное уравнение гидростатики
Умножим дифференциальные уравнения равновесия жидкости Эйлера на 
соответственно и сложим (по размерности имеем: 
– сила, действующая на единичную массу, 
– путь, результат умножения – работа)
Давление 
зависит от координат, т.е. 
.
Полный дифференциал давления (из математики): 
.
Имеем: 
– уравнение равновесия жидкости Эйлера в объединенном виде.
Воспользуемся полученным уравнением для частного случая, когда из массовых сил на жидкость действует только сила тяжести. На элементарную массу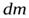 
действует сила веса 
в направлении, противоположном оси 
. Потенциал массовых сил (отношение сил к массе) в проекциях на оси координат: 
, 
, 
.
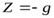Подставляем в объединенное уравнение Эйлера 
или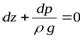 
После интегрирования получаем основное уравнение гидростатики. Для всех точек покоящейся жидкости сумма геометрического и пьезометрического напоров есть величина постоянная 
– гидростатический напор.
Давление абсолютное, избыточное и вакуумметрическое.
На поверхности Земли действует атмосферное давление. Все тела находятся под действием давления столба воздуха. На поверхность жидкости в открытом сосуде всегда действует атмосферное давление, в закрытом сосуде давление может быть как больше атмосферного (избыточное давление) так и меньше атмосферного (вакуумметрическое давление).
| На графике представим перечисленные случаи.
Ось абсцисс графика –
абсолютный вакуум (нет давления).
На оси отметим атмосферное давление  .
|
Точка А –абсолютное давление выше атмосферного, избыточное характеризует превышение абсолютного давления над атмосферным, иногда называется манометрическим.
Точка В – абсолютное давление равно атмосферному. Избыточное равно нулю.
Точка С – абсолютное давление меньше атмосферного (вакуум). Вакуумметрическое давление характеризует на сколько абсолютное давление меньше атмосферного. (избыточное давление отсутствует, формально оно отрицательно).
Определения.
Давление абсолютное – характеризует интенсивность напряженного состояния жидкости, отсчитывается от абсолютного нуля давления. (редко: фактическое, реальное).
Давление атмосферное – давление воздуха на поверхности Земли. Принимается равным 1 кг/см2 – техническая атмосфера (98,0665 кПа, 735,559 мм рт. ст.). Редко используется физическая атмосфера = 760 мм рт.ст.
Давление избыточное (манометрическое) – превышение над атмосферным. 
.
Давление вакуумметрическое (вакуум) – недостаток до атмосферного.
.
Тема 2. Уравнение Бернулли для потока реальной жидкости. Уравнение Бернулли для потока реальной жидкости
В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т.е. напор потока Hпотока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора Δh составят:
,
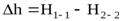где H1-1 - напор в первом сечении потока жидкости,
H2-2 - напор во втором сечении потока,
∆ h - потерянный напор - энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.
С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть
Индексами 1 и 2 обозначены характеристики потока в сечениях 1-1 и 2-2.
Если учесть, что характеристики потока V и α зависят от геометрии потока, которая для напорных потоков определяется геометрией трубопровода, понятно, что потери энергии (напора) в разных трубопроводах будут изменяться неодинаково. Показателем изменения напора потока является гидравлический уклонI, который характеризует потери напора на единице длины потока. Физический смысл гидравлического уклона – интенсивность рассеяния энергии по длине потока. Другими словами, величина I показывает, как быстро трубопровод поглощает энергию потока, протекающего в нём
.
Изменение энергии по длине потока удобно проследить на графиках. Из уравнения Бернулли для потока реальной жидкости(закона сохранения энергии) видно, что гидродинамическая линия для потока реальной жидкости (с одним источником энергии) всегда ниспадающая. То же справедливо и для пьезометрической линии, но только в случае равномерного движения, когда скоростной напор 
а уменьшение напора происходит только за счёт изменения потенциальной энергии потока, главным образом за счёт уменьшения давления P.
Пьезометрическим уклоном называют изменение удельной потенциальной энергии жидкости вдоль потока, приходящееся на единицу его длины.
Если гидравлический уклон всегда положителен, то пьезометрический может быть и положительным, и отрицательным. При равномерном движении жидкости, когда скорость по длине потока не изменяется, скоростной напор вдоль потока a v2/ (2g) = const. Следовательно, пьезометрическая линия параллельна энергетической, и пьезометрический уклон равен гидравлическому.
Изменение удельной потенциальной энергии положения вдоль потока жидкости, приходящееся на единицу длины, называют геометрическим уклоном i и определяют по формуле
где l — расстояние между сечениями потока.
Сформулируем два условия применимости к потоку жидкости уравнения Бернулли: 1) движение жидкости должно быть установившимся; 2) движение жидкости в сечениях 1—2, 2—2 и 3—3, cоединяемых уравнением Бернулли, должно быть параллельно струйным или плавноизменяющимся, в промежутке же между сечениями 1—1, 2—2 и 3—3 движение жидкости может быть и резко меняющимся.
Hа применении уравнения Бернулли основан принцип действия приборов для измерения скоростей и расходов жидкости. Одним из таких приборов является расходомер Вентури, состоящий из двух конических отрезков трубы, узкие концы которых соединены коротким цилиндрическим патрубком длиной менее 10 диаметров трубопровода (отношение диаметра конфузора и диффузора соответственно d/D=:0,3...0,7 ). Принцип работы расходомера Вентури базируется на уравнении Бернулли и уравнении неразрывности потока, а также на том, что перепад давлений на диафрагме, измеряемый пьезометром либо дифманометром пропорционален квадрату протекающего через нее расхода
Для определения местных скоростей при плавноизменяющемся безнапорном движении применяют метод Пито. Трубку, нижний конец которой изогнут под прямым углом, опускают навстречу потоку, и жидкость в трубке начинает подниматься над свободной поверхностью, где давление равно атмосферному, на высоту 
.
При определении местных скоростей в напорном потоке используют систему из двух трубок, одна из которых представляет собой обычный пьезометр, показывающий напор Р/ g, а другая,только что описанная, измеряет величину напора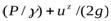 
Разность уровней в обеих трубках h представляет собой скоростной напор 
Местные скорости находят с помощью трубки Пито по формуле
где k- поправочный коэффициент, определяемый для каждой трубки опытным путем
